Дифференцируемость функции в точке.

ЛЕКЦИЯ 8

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ.

ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНЫХ ФУНКЦИЙ

Дифференцируемость функции в точке

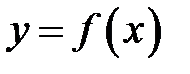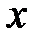Определение 8.1.Функции , определенная при всех , называется дифференцируемой в точке , если приращение 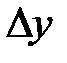этой функции в точке 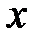, соответствующее приращению аргумента 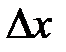, может быть представлено в виде

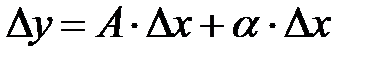, (8.1)

где 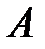– некоторое число, не зависящее от 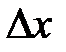, а 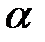– функция аргумента 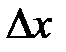, которая является бесконечно малой при .

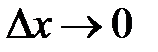Известно, что произведение двух бесконечно малых функций является бесконечно малой функцией более высокого порядка, т.е. 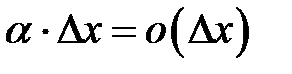. Тогда равенство (8.1) можно переписать в виде .

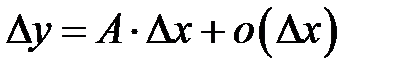Необходимые и достаточные условия дифференцируемости функции в точке

Теорема 8.1. Для того чтобы функция 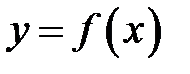была дифференцируема в точке 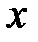, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Доказательство. Необходимость. Пусть функция дифференцируема в точке 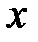, тогда ее приращение представимо в виде (8.1). Рассмотрим отношение .

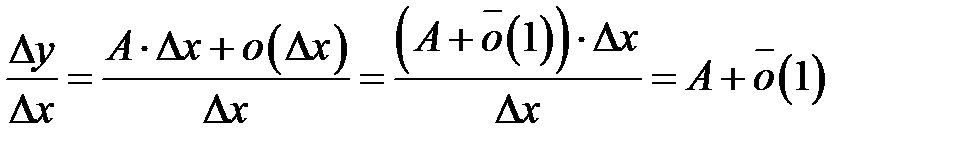Из этого равенства следует, что существует предел левой части. Следовательно, существует производная .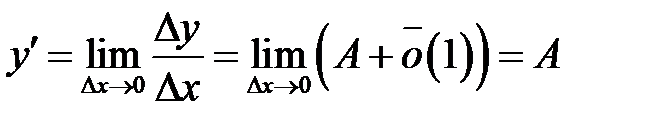

Достаточность. Пусть функция 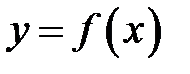имеет в точке 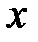конечную производную, т.е. существует предел . По теореме о связи функции, имеющей предел, и бесконечно малой функции можно записать

, где при 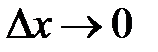. Умножая на 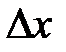обе части последнего равенства, получаем .

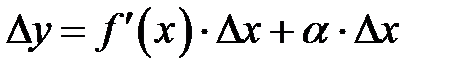Если обозначить – число, которое не зависит от , то получим формулу (8.1), что соответствует определению дифференцируемости функция 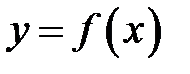в точке 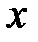. Теорема доказана.

Замечание 8.1.Втеореме 8.1 получена формула 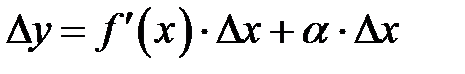, выражающая приращение 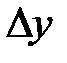функции 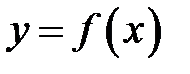в точке 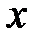, соответствующее приращению аргумента 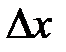, через значение производной этой функции. Тогда формула (8.1) при примет следующий вид:

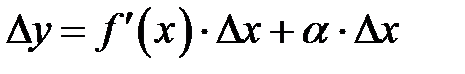(8.1.1)

Теорема 8.1 позволяет отождествлять понятия дифференцируемости функция 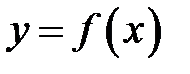в точке 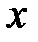с понятием и существования у функции производной в точке .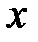

Замечание 8.2.В лекции 7 в примере 7.1 рассмотрена непрерывная в каждой точке функция

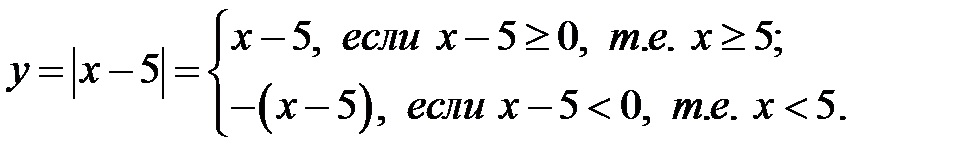
Было показано, при эта функцияне имеет производной, т.к. она имеет левую производную 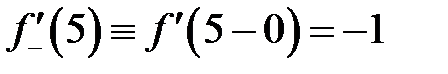и правую производную . Следовательно, данная функция не дифференцируема при .

Производные гиперболических функций

Гиперболические функции встречаются в механике, электротехнике и других технических дисциплинах. Многие формулы для гиперболических функций похожи на формулы для тригонометрических функций, кроме свойства ограниченности.

№	Функция	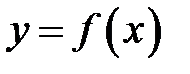Название	Производная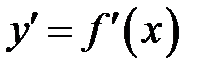
1.		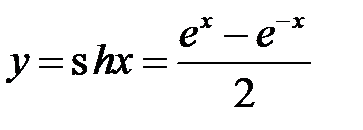гиперболический синус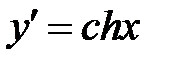
2.		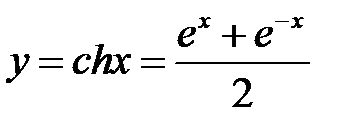гиперболический косинус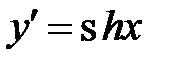
3.		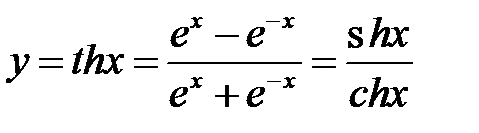гиперболический тангенс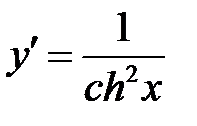
4.		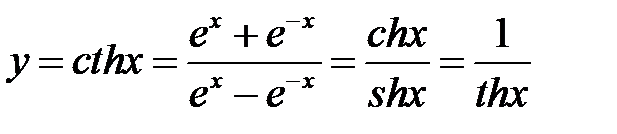гиперболический котангенс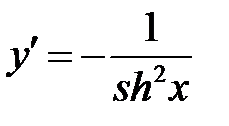

Дифференциал функции

Пусть функция 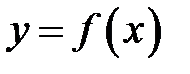– дифференцируема в точке 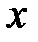, тогда её приращение 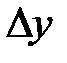этой функции в точке 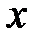, соответствующее приращению аргумента 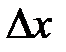, может быть представлено в виде

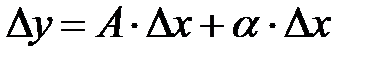, (8.1)

где 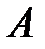– некоторое число, не зависящее от 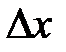, а 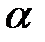– функция аргумента 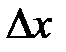, которая является бесконечно малой при .

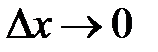Таким образом, приращение 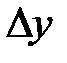функции 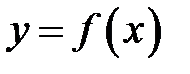представляет собой сумму двух бесконечно малых слагаемых 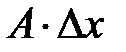и 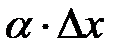. Было показано, что второе слагаемое 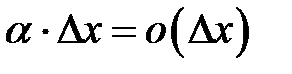является бесконечно малой функцией более высокого порядка, чем т.е. 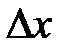(см. 8.1). Поэтому первое слагаемое 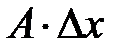является главной линейной частью приращения 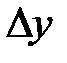функции 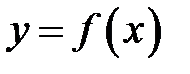. В замечании 8.1. получена другая формула (8.1.1) для приращения 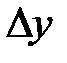функции 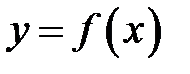, а именно: 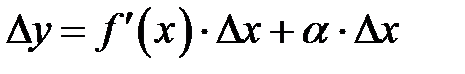. (8.1.1)

Определение 8.3.Дифференциаломфункции 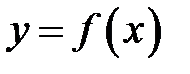в точке 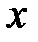называется главная линейная частью её приращения, равная произведению производной 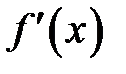в этой точке 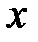на произвольное приращение 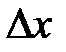аргумента 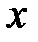, и обозначается 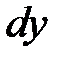(или ):

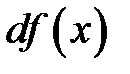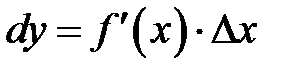(8.4)

Дифференциал 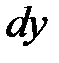функции 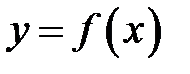называют также дифференциалом первого порядка.

Под дифференциалом 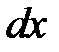независимой переменной 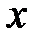понимается любое, независящее от 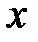, число. Чаще всего, в качестве этого числа берётся приращение переменной 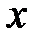, т.е. 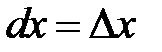. Это согласуется с правилом(8.4) нахождения дифференциала функции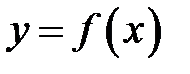

Рассмотрим функцию 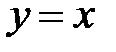и найдем её дифференциал.

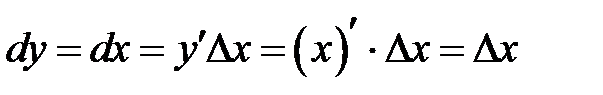, т.к. производная 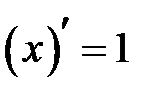. Таким образом, получили: 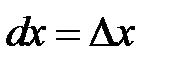и дифференциал 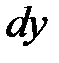функции 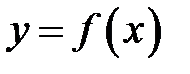можно находить по формуле

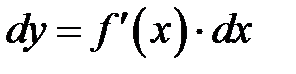. (8.4.1)

Замечание 8.7.Из формулу (8.4.1) следует, что.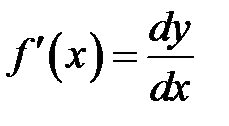

Таким образом, запись 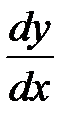можно понимать не только как обозначение для производной 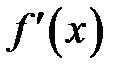, но и как отношение дифференциалов зависимого и независимого переменных.

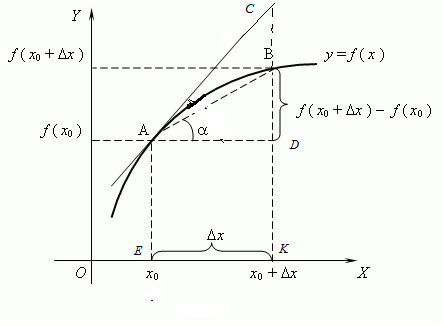
8.7. Геометрический смысл дифференциала функции

Пусть к графику функции 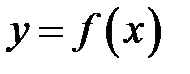проведена (см. рис. 8.1) касательная . Точка 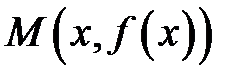находится на графике функции 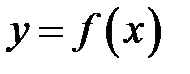и имеет абсциссу – 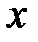. Даем 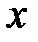произвольное приращение 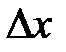, такое, чтобы точка 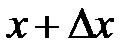не вышла из области определения функции .

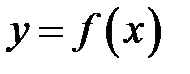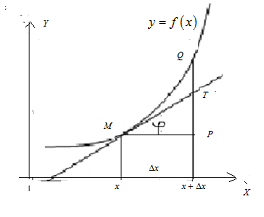
Рисунок 8.1 Изображение графика функции

Точка 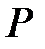имеет координаты 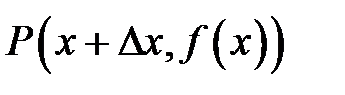. Отрезок 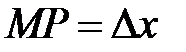. Точка 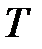лежит на касательной к графику функции 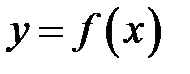и имеет абсциссу – 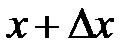. Из прямоугольного следует, что 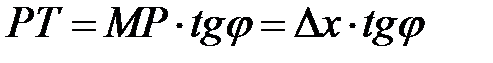, где угол 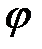– угол между положительным направлением оси 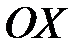и касательной, проведенной к графику функции 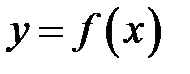в точке 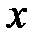. По определению дифференциала 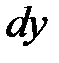функции 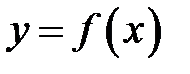и геометрического смысла производной функции 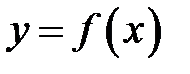в точке 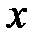, делаем вывод, что 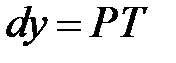. Таким образом, геометрический смысл дифференциала функции 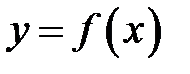заключается в том, что дифференциал 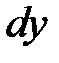представляет собойприращение ординаты касательной к графику функции 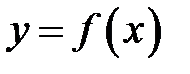в точке .

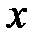Замечание 8.8.Дифференциал 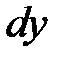и приращение 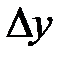для произвольной функции 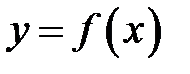, вообще говоря, не равны между собой.В общем случае, разность между приращением и дифференциалом функции является бесконечно малой высшего порядка малости, чем приращение аргумента. Из определения 8.1следует, что 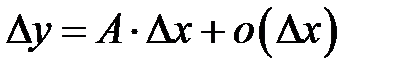, т.е. .

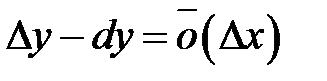На рисунке 8.1точка 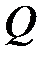лежит на графике функции 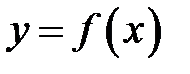и имеет координаты 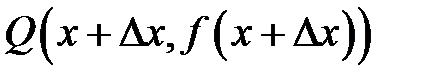. Отрезок .

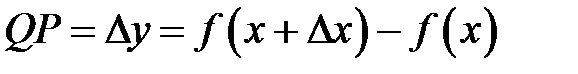На рисунке 8.1 выполнено неравенство 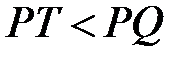, т.е. 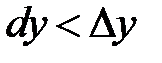. Но возможны случаи, когда справедливо противоположное неравенство 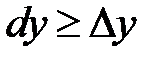. Это выполняется для линейной функции и для выпуклой вверх функции.

ЛЕКЦИЯ 8

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ.