Геометрическая интерпретация комплексных чисел

Если для изображения действительных чисел необходима числовая прямая, то для геометрической интерпретации комплексных чисел требуется плоскость. Всякое комплексное число 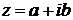можно изобразить как точку на плоскости с координатами a и b (или как вектор ). Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy – мнимой осью.

Изобразим на комплексной плоскости число 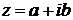. Для определённости и простоты объяснений считаем, что : четверти, т.е. расположим его в первой координатной (см. рис. 2.3).

Рисунок 2.3. Изображение комплексного числа

Комплексное число (0, 1) обозначается символом i = (0, 1) - мнимая единица. Произведение .

Эквивалентность двух приведенных определений комплексных чисел следует из того, что произвольное комплексное число z , заданное упорядоченная парой (x, y) действительных чисел x и y, можно записать в алгебраической форме: z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.

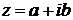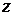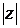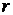Определение 2.3.Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости. Иначе, модуль – это длина радиус-вектора, который соединяет начала координат и соответствующую точку комплексной плоскости. Модуль комплексного числа стандартно обозначают: или или 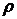. По теореме Пифагора для получаем формулу для нахождения модуля комплексного числа: , которая справедлива для любых значений 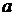и или .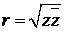

Определение 2.4.Аргументом комплексного числа 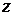называется угол между положительной полуосью действительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

Аргумент комплексного числа 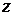стандартно обозначают: или . Из геометрических соображений получается следующая формула для нахождения аргумента: . Данная формула справедлива только в правой полуплоскости. Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.

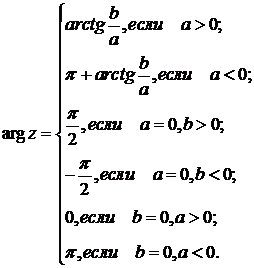
(Здесь функция 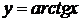– это главный угол или дуга, тангенс которого равен 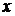: 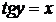и, который изменяется в интервале 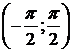, т.е. ).

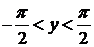Для 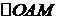(AM=OB) получаем формулы 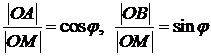, отсюда следует, что . Подставляя последние формулы в алгебраическую форму комплексного числа, получаем тригонометрическую форму записи комплексного числа: .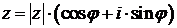
Умножение комплексных чисел, записанных в тригонометрической форме, выполняется стандартным образом, а далее используются тригонометрические формулы: косинус суммы и синус суммы. Получаем:

Эта формула справедлива не только для произведения 2-х комплексных чисел, но и для любого числа комплексных чисел, т.е. при умножении комплексных чисел их модули перемножаются, а их аргументы складываются.

Если перемножать 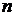одинаковых комплексных чисел, то получается формула Муавра: формула возведения комплексного числа в степень : .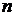

Для того, чтобы комплексное число возвести в степень 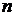необходимо возвести в степень 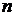модуль этого числа, а аргумент умножить на .