Эквивалентные состояния и автоматы.

Два состояния q_i и q_j называются эквивалентными, если выполняется равенство: S (q_i, a ) = S (q_j, a ) для произвольного a.

В простейшем случае , когда входящее слово состоит из одной буквы, эквивалентность имеет вид: l (q_i,a) = l (q_j,a)

Множестваво всех эквивалентных состояниях называются классом эквивалентности К.

Допустим q_i и q_j принадлежит классу К₀ ,сформируем слово a следующим образом a = а₀а₁, тогда согласно определению эквивалентности мы можем записать.

S ( q_i, а₀, а₁) = S ( q_j, а₀, а₁)

Полученное равенство запишем в ином виде :

l ( q_i, а₀ ) l ( q_i, а₀, а₁) = l ( q_j, а₀ ) l ( q_j, а₀, а₁)

Исходя из определения эквивалентности : выполняется равенство:

l ( q_i, а₀ ) = l ( q_j, а₀ ),

а значит выполняется и равенство:

l ( q_i, а₀, а₁) = l ( q_j, а₀, a₁ )

Преобразовав получим равенство :

l ( d ( q_i, а₀ ), а₁) = l ( d ( q_j, а₀ ), а₁)

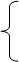Для того, чтобы две составляющие q_i и q_j были эквивалентны, должны выполнятся следующие условия :

l ( q_i, а ) = l ( q_j, а )

d ( q_i, а ) = d ( q_j, а ) Î K

Используя свойства эквивалентных состояний, множество сост. заданного автомата всегда может быть разбито на соответствующие классы эквивалентности.

Рассмотрим следующий пример :

Автомат задан графом вида :

А = {0, 1}; V = {0, 1}

Q = { q₁, q₂, q₃, q₄, q₅, q₆, q₇ }

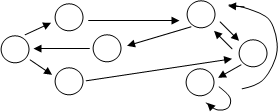q₂ q₆

q₁ q₄ q₇

q₃ q₅

Составим таблицы выходов и функции перехода :

l	q1	q2	q3	q4	q5	q6	q7

d	q1	q2	q3	q4	q5	q6	q7
	q2	q5	q7	q1	q5	q4	q5
	q3	q6	q4	q3	q6	q7	q6

Используя два условия эквивалентности разобьем множество сост. автоматов на классы эквивалентности :

1. Получение класса условно эквивалентных сост. ( проверяем условие выполнения первого равенства ). Используя таблицу выходов мы можем записать два условно эквивалентных класса.

к₀ = {q₁ q₂ q₅}

к₁ = {q₃ q₄ q₆ q₇}

2. Проверка эквивалентности полученных классов:

d	q1	q2	q3	q4	q5	q6	q7
	к0	к0	к1	к0	к0	к1	к0
	к1	к1	к1	к1	к1	к1	к1

На основании полученной таблицы и второго условия эквивалентности

делаем вывод : класс к₁ распадается на два класса :

к₁^, = {q₃ q₆} к₁^” = { q₄ q₇}

3. С учетом нового разбиения на классы опять заполняется таблмца перехода :

d	q1	q2	q3	q4	q5	q6	q7
	к0	к0	к1”	к0	к0	к1”	к0
	к1’	к1’	к0	к1’	к1’	к1”	к1’

В результате решения задачи получены три класса эквивалентности :

к₀ = { q₁, q₂, q₅}

к₁^’ = { q₃ q₆}

к₁^” = { q₄ q₇}

Для проверки подадим на вход последовательность :

	q1	q2	q6	q7	q6	q4	q3	q4	q1	q2
a
w

	q5	q3	q6	q7	q6	q4	q3	q4	q1	q2
a
w

Автоматы S и Т называются эквивалентными, если любому сост. автомата S найдется сост. автомата Т. ( и наоборот)

Если автомат S₀ эквивалентен автомату S и количество сост. S₀ > S, то S₀ – минимальный автомат ( единственный ).

Построим мин. автомат S₀ для нашего примера:

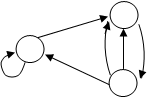q₀₁ ® k₀ q₀₂ ® k₁’ q₀₃ ® k₁^”

q₀₂

q₀₁

q₀₃

l0	q01	q02	q03

d	q01	q02	q03
	q01	q03	q01
	q02	q03	q02

РЕАЛИЗАЦИЯ КА.

КА состоит из двух остальных блоков:

1. реализует функцию переходов;

2. реализует функцию выходов.

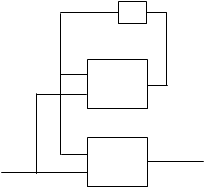t

_{qi d (qi, aj)}

^aj

_qi

_{aj aj} ^{l (qi, aj)} v_k

В этой схеме используют устройство, реализующее задержку перехода автомата в новое состояние на время t.

Если t одинаково для любых состояний, то автомат синхронный, иначе асинхронный.

Блок функций выходов и переходовмогут быть реализованы комбинаторными системами.