Методы расчета турбулентных струй

Интегральные методы расчета

Сложный характер турбулентного движения, которое пока не удается описать единой системой дифференциальных уравнений, обусловил широкое использование интегральных методов. Отличительной особенностью этих методов является задание в какой-либо форме профилей газодинамических параметров или их комбинаций. Это позволяет исключить из рассмотрения дифференциальные уравнения движения, энергии и диффузии и ограничиться использованием интегральных соотношений.

Проиллюстрируем применение метода интегральных соотношений к расчету основного участка струи, истекающей в затопленное пространство. На этом участке линейные размеры сопла пренебрежимо малы по сравнению с расстоянием от него, что позволяет считать течение автомодельным и принять срез сопла за точечный источник массы, количества движения и энергии.

Запишем выведенные ранее (см. формулы (2.2.9) – (2.2.13), (2.4.11), (2.5.9)) интегральные законы сохранения количества движения, энергии и массы для изобарических участков сжимаемых неизотермических струй или струй с диффузионным факелом горения:

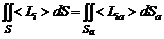, (3.1.1)

где 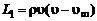, , 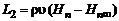, , 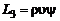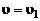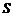– площадь струи в произвольном поперечном сечении на изобарическом участке, 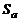– площадь начального сечения изобарического участка.

Для струй, истекающих в затопленное пространство, 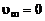, суммарное количество движения в сечении 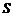равно реактивной силе (см. формулу (2.2.12))

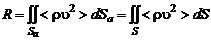. (3.1.2)

На основе опыта установлено, что для турбулентной струи на достаточно больших удалениях от среза сопла характер изменения математических ожиданий комплексов 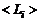по сечению струи на основном участке хорошо описывается экспоненциальными зависимостями вида

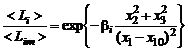, (3.1.3)

где индексом «m» обозначены параметры на оси; начало координат совмещено с центром выходного сечения сопла; 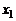– продольная координата, совпадающая с осью струи и отсчитываемая от среза сопла; 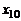– опытная константа, определяющая полюс струи; 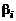– опытные константы.

Дополним (3.1.1) – (3.1.3) уравнением состояния, которое для изобарического участка струи имеет вид

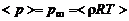, (3.1.4)

и термодинамическими зависимостями, определяющими 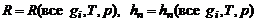– для струй с физико-химическими превращениями,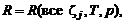 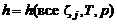– для неизотермических струй без физико-химических превращений. Если теперь выразить математические ожидания комбинаций газодинамических параметров через математические ожидания этих параметров, то система (3.1.1) – (3.1.4) становится замкнутой и, решая её, находим искомые средние значения газодинамических параметров в требуемых точках основного участка струи.

В работах, в которых используются интегральные методы расчета струйных течений, явно или неявно предполагается, что математические ожидания произведений газодинамических параметров равны произведениям математических ожиданий. Обычно это предположение не приводит к значительным ошибкам при определении математических ожиданий газодинамических параметров. Однако возможны реальные ситуации, в которых указанное предположение делать нельзя. Например, при истечении водородной струи в воздух диффузионный факел располагается вблизи наружной границы струи и температура в факеле вследствие пульсаций газодинамических параметров снижается почти на 1000 К.

Аналогичным образом определяются газодинамические параметры в зонах смешения на начальном участке турбулентной струи. Автомодельными зонами струи в этом случае являются пограничные слои, развивающиеся на поверхностях тангенциальных разрывов скорости. Профили 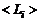в сечениях пограничного слоя задаются зависимостями, полученными на основании обработки опытных данных.

При расчете блочных струй используется согласующийся с интегральными законами сохранения (3.1.1) и подтвержденный экспериментальными исследованиями принцип суперпозиции решений для комплексов :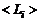

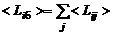, (3.1.5)

где 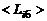– значение комплекса 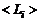в заданной точке при работе всех двигателей, входящих в блок, 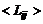– при работе лишь j-го двигателя блока.

Отметим, что, разбивая начальное сечение изобарического участка турбулентной струи на элементарные струйки, используя соотношения типа (3.1.1) для основного участка j-й струйки и выполняя суммирование комплексов 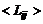в соответствии с формулой (3.1.5), можно найти распределение 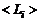по всему полю, в том числе и на неавтомодельных участках, при произвольном законе распределения 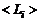в начальном сечении.

Метод интегральных соотношений, базирующийся на зависимостях вида (3.1.1), может быть распространен с соответствующими видоизменениями, связанными с наличием продольного градиента давления, на струи в сносящем потоке.

Возможны и другие формы зависимостей, определяющих профили газодинамических параметров по сечению струи.
Так, например, в работах Г.И. Абрамовича задаются профи-
ли 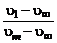, , 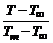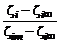. В работах А.С. Гиневского

постулируется полиномиальный закон изменения турбулентного трения по сечению струи, что, с использованием гипотезы Прандтля о связи турбулентного трения с поперечным градиентом осредненной скорости, при соответствующих граничных условиях определяет, в конечном счете, профиль средней скорости. Известен еще ряд способов задания как аппроксимирующих зависимостей, так и комбинаций газодинамических параметров, для которых эти зависимости определены.

Вычисление среднеквадратических значений пульсаций газодинамических параметров и прочих вероятностных характеристик требует введения самостоятельных гипотез.

Среднеквадратическое значение пульсации 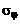некоторой величины 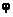обычно находится с помощью предположения о пропорциональности 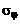поперечному градиенту математического ожидания 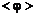. Коэффициент пропорциональности, в общем случае зависящий от координат выбранной точки и параметров на срезе сопла и окружающей среды, определяется по соотношениям, обобщающим экспериментальные результаты. В практике расчетов турбулентных струй широко используется, например, выражение для 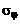на базе полуэмпирической теории Прандтля:

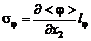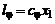; , (3.1.6)

где 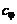– опытная константа, 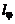– путь смешения.

Следует заметить, что для струй с диффузионными факелом предположение о пропорциональности 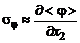слишком грубо и приводит к большим количественным, а в ряде случаев и качественным ошибкам в определении среднеквадратических величин пульсаций в значительных областях. Так, в зоне диффузионного факела горения поперечные градиенты математических ожиданий плотности 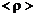и температуры 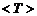равны нулю, в то время как среднеквадратические значения пульсаций плотности 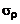и температуры 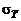в этих областях близки к максимальным. Аналогичная картина наблюдается, в частности, и на основном участке струи: пульсации газодинамических параметров на оси достаточно велики, в то время как соответствующие градиенты математических ожиданий в силу симметрии равны нулю.

В зоне смешения блочных струй по сечению может наблюдаться еще больше (пять и более) зон с нулевыми градиентами 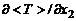и и 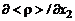значительными величинам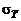и и .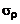

Все это существенно ограничивает возможности применения соотношений типа (3.1.6) для определения среднеквадратических значений пульсаций газодинамических параметров в струях с диффузионным факелом.

Известны попытки "исправить" соотношения (3.1.6) введением слагаемых, пропорциональных второй производной от 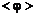, что позволяет получить ненулевые значения 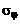при нулевых градиентах величины 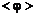. Однако формулы подобного типа не получили широкого распространения из-за сложности расчетных соотношений и необходимости введения еще ряда эмпирических констант. К тому же эти формулы недостаточно универсальны.

В заключение обратим внимание на сильные и слабые стороны интегральных методов, имея в виду их использование при создании пакета прикладных программ.

Интегральные методы позволяют с достаточной для технических приложений точностью получить математические ожидания газодинамических параметров или их комбинаций без учета пульсационного движения. В большинстве случаев учет пульсаций не приводит к заметному обратному влиянию на искомые величины. Поэтому задачи определения характеристик осредненного и пульсационного движения могут решаться раздельно.

Основной недостаток метода интегральных соотношений - большие ошибки при определении характеристик пульсационного движения, часть из которых, например характерные масштабы пульсационного движения, в рамках интегральных методов вообще не определяются.

Наибольшей универсальностью обладает метод расчёта, основанный на использовании соотношений (3.1.1) – (3.1.5). По ним рассчитываются математические ожидания газодинамических параметров на автомодельных и неавтомодельных изобарических участках различных типов струй, включая блочные струи. Другие интегральные методы, рассмотренные ранее, например методы, основанные на задании профилей скорости и температуры, заметно меньше распространены: они используются лишь для определения газодинамических параметров на автомодельных участках одиночных струй.

Опытные константы, входящие в расчетные зависимости интегральных методов, зависят от числа Маха на срезе сопла, нерасчетности, отношения плотностей на срезе сопла и в окружающей среде, числа Маха спутного потока и т.д. Интересно отметить, что количество опытных констант и набор факторов, влияющих на их величину, примерно одинаковы не только для интегральных методов, но и для рассматриваемых далее полуэмпирических моделей расчета турбулентных струй.

Основное положительное свойство интегральных методов - возможность определения газодинамических и электрофизических параметров только в требуемых точках струй и по достаточно простым зависимостям даже для трехмерных струй. В результате избыточная информация в процессе счета исключается, а время на проведение расчетов существенно сокращается.

3.2. Полуэмпирические методы расчета, основанные
на уравнениях для рейнольдсовых напряжений

Определение математических ожиданий газодинамических параметров, а в ряде случаев и моментов более высокого порядка, в турбулентных течениях, в том числе и в турбулентных струях, с помощью уравнений Рейнольдса и замыкающих условий разной степени сложности сформировалось в теории турбулентных течений в самостоятельное направление. Появилось множество полуэмпирических теорий турбулентности, существо которых состоит в замыкании уравнений Рейнольдса с помощью дополнительных соотношений.

Рассмотрим некоторые из них для несжимаемой жидкости.

Итак, уравнения неразрывности и движения для осредненных параметров (см. формулы (2.6.6) – (2.6.9)) могут быть формально записаны в том же виде, что и для ламинарного движения, но будут содержать симметричный тензор добавочных турбулентных напряжений .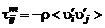

Первую попытку замкнуть систему уравнений движения, связав тензор 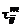с параметрами осредненного движения, сделал Буссинеск в 1877 г. еще до появления работы Рейнольдса. Согласно гипотезе Буссинеска, между тензором турбулентных напряжений и тензором осредненных скоростей деформации существует связь, аналогичная линейной связи между тензором вязких напряжений и тензором скоростей деформации ламинарного течения:

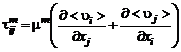. (3.2.1)

В отличие от ламинарного течения, коэффициент турбулентной вязкости 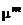не является постоянной величиной, а определяется начальными и граничными условиями, характером движения и в общем случае представляет собой скалярную функцию координат пространства.

При развитом турбулентном течении, в достаточном удалении от стенок, напряжения молекулярной вязкости пренебрежимо малы по сравнению с турбулентными. Это позволяет опустить в (2.6.6) член 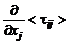. В результате получим уравнения Буссинеска:

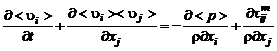, (3.2.2)

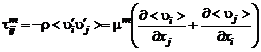, (3.2.3)

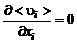. (3.2.4)

Однако формула (3.2.3), написанная по аналогии с ламинарным течением несжимаемой жидкости, не вполне корректна. Это связано с тем, что, в отличие от ламинарного течения, сумма нормальных компонентов турбулентных сил трения не равна нулю:

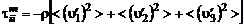. (3.2.5)

Так как кинетическая энергия турбулентности в единице массы равна:

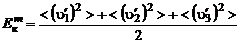, (3.2.6)

то

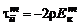. (3.2.7)

Для устранения указанной некорректности А.Н. Колмогоров в 1942 г. предложил новый вариант гипотезы о связи между тензором турбулентных сил трения и тензором скоростей деформации осредненного поля:

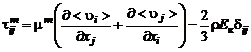, (3.2.8)

где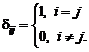

Система уравнений (3.2.2), (3.2.8), (3.2.4) требует для своего замыкания дополнительных зависимостей, определяющих коэффициент турбулентной вязкости 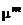и кинетическую энергию турбулентности 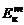. Наибольшей популярностью пользуется
модель, в которой замыкание достигается введением дифференциальных уравнений типа уравнений переноса для 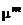и 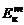( 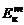– 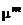модель).

Модели типа 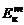– 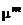обладают высокой универсальностью, позволяя находить математические ожидания газодинамических параметров не только в турбулентных струях, но и в сложных пространственных течениях с большими градиентами давления. Однако эта универсальность достигается введением дополнительного набора опытных констант, зачастую меняющихся в зависимости от характера течения, и требует значительных затрат времени на проведение расчетов без увеличения точности получаемых результатов. Поэтому применение указанной модели для расчета турбулентных струй нецелесообразно.

Уравнения пограничного слоя. В 1904 г. Прандтль упростил уравнения Навье – Стокса применительно к задачам о течении в пограничном слое. Существо этих упрощений сводится к выделению узких зон, называемых пограничными слоями, в которых продольные градиенты газодинамических величин пренебрежимо малы по сравнению с поперечными.

Запишем, например, уравнения Буссинеска – Колмогорова для стационарной плоскопараллельной турбулентной струи несжимаемой жидкости или газа с учетом приближений пограничного слоя:

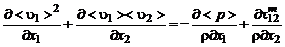,(3.2.9)

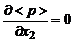, (3.2.10)

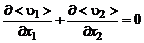, (3.2.11)

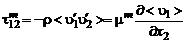, (3.2.12)

где 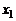– продольная координата, отсчитываемая от среза сопла по оси струи или параллельно ей; 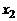– поперечная координата.

К настоящему времени известно много теорий струйной или так называемой свободной турбулентности, основанных на замыкании системы уравнений пограничного слоя. Остановимся на трех: старой теории Прандтля, теории Тейлора и новой теории Прандтля, как получивших наибольшее признание и широко используемых. Для удобства и наглядности суть рассматриваемых теорий поясним на примере простейшего типа струйного тече-ния – течения в стационарной плоскопараллельной изобарической струе несжимаемой жидкости.

Старая теория свободной турбулентности Прандтля.Займемся анализом формулы (3.2.12) для турбулентного трения. Введем среднеквадратические значения пульсаций скорости в продольном и поперечном направлениях:

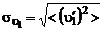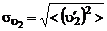, . (3.2.13)

Корреляционная функция 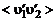может быть представлена в нормированном виде:

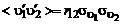, (3.2.14)

где 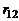– коэффициент корреляции, который по определению меняется в пределах 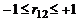. Прандтль предложил считать коэффициент корреляции 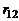равным 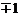. Знак «минус» соответствует положительному градиенту продольной скорости 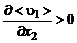, а «плюс» – отрицательному 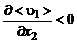. Поясним это предположение. Пусть 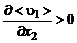. Тогда жидкие частицы, перемещаясь в положительном направлении оси 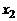, , 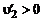вызывают отрицательные пульсации продольной составляющей скорости 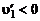и, наоборот, если 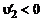, то 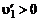. Такое же рассуждение для 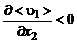приводит к одинаковым знакам пр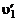и и .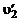

В свою очередь величина 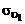предполагается пропорциональной модулю градиента осредненной продольной скорости в поперечном направлении:

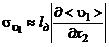. (3.2.15)

Названный Прандтлем "путь смешения" 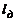в рассматриваемой модели линейно зависит от продольной координаты:

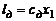, (3.2.16)

где 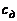– единственная эмпирическая постоянная теории свободной турбулентности Прандтля.

Подставляя (3.2.16), (3.2.15), (3.2.14) в (3.2.12) и предполагая равенство 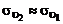, получим следующую известную формулу турбулентного трения Прандтля:

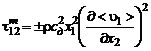. (3.2.17)

Здесь знак «плюс» берется при 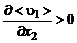. Формулу (3.2.17) можно записать в ином виде:

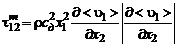. (3.2.18)

Используя выражение для турбулентного трения (3.2.18) и подставляя его в (3.2.9) при 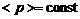, получим замкнутую систему двух уравнений, описывающую поле скоростей в плоской струе несжимаемой жидкости:

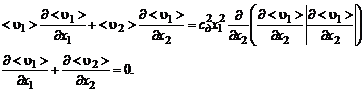(3.2.19)

Толмин применил старую теорию свободной турбулентности Прандтля к решению трех задач о распространении свободных затопленных струй несжимаемой жидкости: о пограничном слое беспредельной плоской струи; о плоской струе, вытекающей из очень узкого отверстия; об осесимметричной струе, вытекающей из очень узкого отверстия. Во всех случаях Толмину удалось подбором одной опытной константы 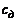добиться хорошего согласия экспериментальных и теоретических результатов.

Теория Прандтля может быть обобщена на решение тепловой и диффузионных задач.

Для отыскания закона распределения температур в плоской струе воспользуемся уравнением энергии (2.4.12) с учетом следующих допущений (помимо тех, которые уже приняты: , , 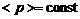движение установившееся, струя плоская):

· скорости малы, что позволяет пренебречь кинетической энергией в выражении для полного теплосодержания:

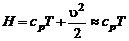; (3.2.20)

· массовые силы пренебрежимо малы: ;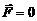

· молекулярной теплопроводностью и переходом работы вязких сил в тепло пренебрегаем вследствие их малости по сравнению с турбулентным переносом тепла;

· объемное выделение тепла равно нулю: .

Выполнив операцию осреднения газодинамических параметров и их комбинаций, получим уравнение энергии для плоского пограничного слоя в виде

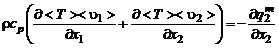, (3.2.21)

где турбулентный тепловой поток в поперечном направлении равен:

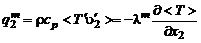. (3.2.22)

Здесь 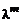– коэффициент турбулентной теплопроводности.

Применим подход Прандтля при подборе замыкающего соотношения для корреляционной функции 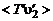. Запишем ее в виде

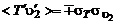, (3.2.23)

где знак «минус» соответствует положительному поперечному градиенту температуры 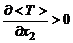; 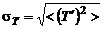– среднеквадратическое значение пульсации температуры.

Полагая, что

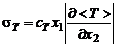, (3.2.24)

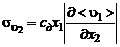, (3.2.25)

получим выражение для корреляционной функции :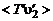

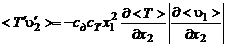. (3.2.26)

Подставляя (3.2.22) и (3.2.26) в (3.2.21) и учитывая уравнение неразрывности (3.2.11), приходим к уравнению энергии для плоской изобарической турбулентной струи:

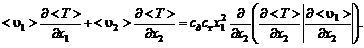(3.2.27)

В формулу (3.2.27) приходятся вводить уже две опытные константы: 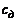и 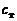, так как, по экспериментальным данным, тепловой турбулентный слой толще динамического. Соответственно турбулентное число Прандтля 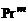, определяемое как отношение:

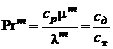, (3.2.28)

меньше единицы (опытное значение ).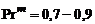

Применив аналогичные рассуждения к уравнению диффузии пассивной примеси (2.5.10), получим уравнение диффузии для плоской турбулентной струи:

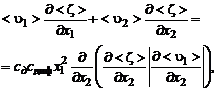(3.2.29)

где 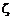– массовая концентрация пассивной примеси.

Сопоставление полученных из опыта профилей нормированных избыточных температур 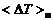и массовой концентрации пассивной примеси 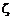показало их идентичность, что позволяет считать

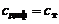, (3.2.30)

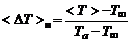, (3.2.31)

где 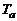– температура на срезе сопла, 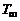– температура окружающей среды.

Таким образом, решение динамической, тепловой и диффузионных задач в рамках старой теории турбулентности Прандтля требует введения двух опытных констант: 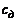и .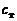

Теория свободной турбулентности Тейлора. Физическая модель турбулентности Тейлора исходит из предположения, что турбулентное трение вызывается переносом вихрей, а не количества движения, как в старой теории свободной турбулентности Прандтля. В результате Тейлор получил уравнения движения, энергии и диффузии эквивалентные соответствующим уравнениям старой теории Прандтля при условии 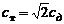. Турбулентное число Прандтля в теории Тейлора равно 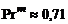, что хорошо согласуется с экспериментальными данными.

Тем самым Тейлор построил замкнутую систему уравнений для определения осредненных газодинамических параметров в струе несжимаемой жидкости, используя лишь одну опытную константу .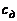

Новая теория свободной турбулентности Прандтля. Новая теория турбулентности Прандтля (1942), базируется на допущении о постоянстве коэффициента турбулентной вязкости 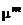по сечению струи:

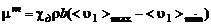, (3.2.32)

где 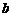– ширина зоны смешения, определяемая по эмпирическим формулам, 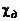– опытная константа.

Уравнение (3.2.32) с точки зрения точности описания течения в турбулентных струях не имеет преимуществ перед соотношением для коэффициента турбулентной вязкости :

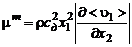, (3.2.33)

используемого в старой теории турбулентности Прандтля, но не приводит к противоречащему действительности требованию обращения 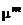в нуль в точках слоя смешения, где .

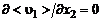3.3. Феноменологическая модель Рейхардта.
Принцип суперпозиции решений

Безуспешные попытки создания общей теории турбулентного движения, даже в рамках несжимаемой жидкости, а также неотложные потребности инженерной практики побудили исследователей заняться построением так называемых феноменологических теорий. Суть этих теорий состоит в том, чтобы, отталкиваясь от экспериментального материала, найти по возможности простые соотношения, генерирующие решения для определенного класса течений.

Наиболее удачная теория такого рода для изобарических турбулентных струй была предложена в 1941 г. Рейхардтом. Он заметил, что распределения скоростей в областях турбулентного перемешивания свободных затопленных струй несжимаемой жидкости достаточно точно описываются уравнениями типа уравнений теплопроводности:

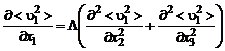, (3.3.1)

где 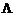– опытный коэффициент, зависящий от продольной координаты.

Формально уравнение Рейхардта (3.3.1) можно получить традиционным методом, осредняя уравнение движения по схеме Рейнольдса.

Покажем это на примере плоской изобарической стационарной струи несжимаемой жидкости.

Запишем уравнение движения струи, отбрасывая члены с молекулярной вязкостью:

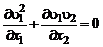. (3.3.2)

После осреднения получим

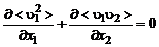. (3.3.3)

Полагая далее, что интенсивность поперечного переноса количества движения пропорциональна поперечному градиенту составляющей количества движения по продольной оси:

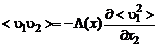, (3.3.4)

приходим к уравнению

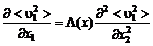, (3.3.5)

которое похоже на уравнение теплопроводности, хотя и сложнее его, так как 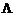зависит от .

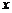В ряде последующих работ метод Рейхардта был обобщен на более сложные типы турбулентных струй: изотермические и неизотермические, затопленные струи и струи, распространяющиеся в спутном потоке, струи с диффузионными факелом горения и т.д. Было показано, что уравнения типа уравнений теплопроводности, записанные в виде

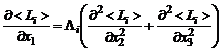, (3.3.6)

позволяют находить распределения газодинамических параметров во всех перечисленных выше случаях. С использованием газодинамических комплексов 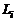автоматически выполняются законы сохранения количества движения, энергии и массы, так как именно эти комплексы входят в интегральные соотношения (3.1.1). Метод Рейхардта, известный в отечественной литературе как метод эквивалентной задачи теории теплопроводности, был обобщен и проверен с привлечением обширного экспериментального материла на различных типах турбулентных струй, в том числе на одиночных и блочных струях, при произвольном профиле распределения параметров в начальном сечении и с учетом возможных физико-химических процессов типа диффузионного горения, диссоциации и ионизации. Накопленный опыт применения уравнений вида (3.3.6) для расчета струйных течений позволяет отметить хорошее соответствие результатов расчета опытным данным.

Наряду с этим многие исследователи обращали внимание на неудовлетворительное физическое обоснование метода Рейхардта. Собственно говоря, сам Рейхардт даже не пытался построить физические модели турбулентного обмена, а ограничился поисками уравнений, которые бы генерировали соответствующие опытным данным распределения газодинамических параметров в турбулентной струе.Такими оказались уравнения типа уравнений теплопроводности. Лишь в дальнейшем появились работы, в которых обсуждался и обосновывался переход от нелинейных дифференциальных уравнений в частных производных пограничного слоя к линейным типа уравнений теплопроводности. В частности, Л.А. Вулис предлагает осуществить такой переход введением некой системы координат, в которой уравнения пограничного слоя преобразуются к виду (3.3.6). Однако предложенная Вулисом модель носит формальный характер и не объясняет физическую сущность процессов, протекающих в струйном пограничном слое.

Причину хорошего соответствия решений уравнений типа уравнений теплопроводности для математических ожиданий комплексов 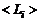опытным данным следует искать в вероятностном характере турбулентного движения.

Действительно, решения уравнений типа уравнений теплопроводности для комплексов 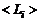удовлетворяют следующим условиям.

1. На больших расстояниях от начального сечения изобарического участка турбулентной струи 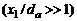распределения комплексов 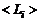по сечениям приближаются к распределениям, даваемым нормальным законом.

2. Справедлив принцип суперпозиции частных решений для комплексов 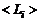(см. формулу (3.1.5)). Принцип суперпозиции частных решений вытекает из линейности уравнений (3.3.6).

Можно показать, что оба сформулированных утверждения непосредственно следуют из известных теорем теории вероятности, если принять во внимание случайный характер движения элементарных масс при переносе их крупномасштабными пульсациями. Так как отклонение каждой такой элементарной массы от линии, параллельной оси струи, – случайная величина, то его можно статистически описать, задав соответствующую плотность вероятности. Из центральной предельной теоремы теории вероятности следует, что после достаточно большого числа пульсаций плотность вероятности отклонения элементарной массы от математического ожидания будет характеризоваться нормальным законом. Если далее предположить, что каждой такой элементарной массе соответствует определенное значение 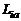, то, по определению математического ожидания случайной величины, придем к первому утверждению. Второе утверждение является следствием теоремы о математическом ожидании суммы случайных величин.

Обратим внимание на следующие два важных момента:

1. Задаваемые в интегральном методе расчета турбулентных струй распределения математических ожиданий комплексов 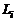в виде соотношений (3.1.3) и (3.1.5) являются решениями уравнений типа уравнений теплопроводности, что легко проверить непосредственной подстановкой этих соотношений в (3.3.6).

2. Линейный характер уравнений типа уравнений теплопроводности позволяет получать аналитические решения на изобарических участках двумерных и трехмерных струй при произвольной форме границы начального сечения и в общем случае неравномерном распределении в нем газодинамических параметров. Поэтому время, затрачиваемое на расчет параметров в струе при использовании полуэмпирической теории турбулентности Рейхардта, существенно меньше, чем при применении других полуэмпирических моделей, оперирующих с нелинейными дифференциальными уравнениями в частных производных. Это обстоятельство и обусловило широкое использование метода Рейхардта в инженерной практике при расчете струйных течений.