ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ ДЛЯ ИССЛЕДОВАНИЯ ФУНКЦИЙ И ПОСТРОЕНИЯ ГРАФИКОВ (решение задач)

Учебное пособие для студентов всех форм обучения для самостоятельной подготовки к выполнению контрольных работ.

Москва 2015

Составитель: к.ф.м.н., доцент Выборнов А.Н..

В этом пособии рассматриваются задачи нахождения наибольших и наименьших значений функций, задачи исследования функций, заданных формулой (элементарных функций) средствами дифференциального исчисления. В приложении рассмотрено применение правила Лопиталя для вычисления пределов. Пособие составлено на основе пособия МГАПИ (Архипов Н.В., Головешкин В.А., Егиазаров Ю.И., Зюзько Т.Н.) для заочного отделения. Составителем исправлены неточности и переработано изложение теоретических положений и методов решения задач. Пособие может использоваться как дополнительное пособие по развитию навыков решения задач.

Напомним определение локального макси­мума и минимума функции.

Точка 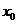называется точкой локального максимума (минимума) функции 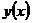, если существует такая окрестность точки 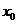, что для всех точек , принадлежащих этой окрестности, выполняется неравенство ( ).

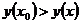Точки локального максимума и локального минимума назы­ваются точками экстремума функции.

Сформулируем теорему о необходимом условии сущест­вование экстремума.

Теорема Ферма (необходимое условие сущест­вования экстремума)

Точками экстремума непрерывной функции могут быть только такие точки, в которых производная этой функции или равна нулю или не существует.

Точки, в которых функция обращается в ноль или терпит разрыв, будем называть критическими точками этой функции.

В следующей задаче требуется найти наибольшее и наименьшее значения функции, заданной на некотором отрезке и непрерывной на этом отрезке.

Из свойств непрерывной функции известно, что функция непрерывная на отрезке принимает на этом отрезке свое наибольшее и наименьшее значения.

Если наибольшее или наименьшее значение достигается внутри отрезка, то эта точка является точкой локального экстремума, а значит критической точкой производной этой функции. Поэтому, для определения наибольшего и наименьшего значений функции на некотором отрезке и непре­рывной на этом отрезке может быть предложена следующая схема:

1. Находим производную функции.

2. Определяем критические точки производной и выбираем те из них, которые лежат внутри данного отрезка.

3. Вычисляем значения функции в выбранных точках и на концах отрезка.

4. Среди вычисленных значений выбираем наибольшее и наименьшее.

Задача.

Найти наибольшее и наименьшее значение функции на заданном отрезке.

.

Решение.

Найдем критические точки производной, для чего вычислим производную функции и приравняем ее нулю:

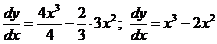
при ,

откуда находим критические точки: .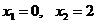

Далее необходимо выбрать те критические точки, которые принадлежат заданному отрезку. В данном случае обе критические точки ему принадлежат. Вычислим значения функции в критических точках и на концах отрезка и выберем наибольшее и наименьшее значения функции:

.

.

.

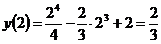Делаем вывод о том, что свое наибольшее значение на заданном отрезке функция достигает при , , 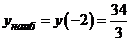а наименьшее значение при , .

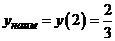Задача.

Найти наибольшее и наименьшее значение функции на заданном отрезке.

, .

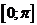Решение.

Находим производную: .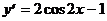

Находим критические точки: ; .

На отрезке 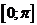лежат , .

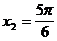Вычисляем значения функции: ; ; ; .

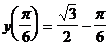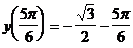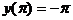Наибольшее значение: .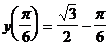

Наименьшее значение: .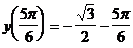

В следующей «текстовой» задаче требуется найти наибольшее или наименьшее значение некоторой величины S( , ), зависящей от двух параметров и . Условия задачи позволяют определить возможную область изменения параметров.

При этом параметры и не являются независимыми, а связаны соотношением F( , )=0, причем из соотношения F( , )=0 один параметр может быть выражен через другой, например: = ( ).

При подстановке = ( ) функция S становится функцией одного параметра , т.е. S=S( , ( )).

Если область возможного изменения параметра является отрезком, то дальнейшее решение проводится по схеме решения предыдущих задач.

Если область изменения параметра является интервалом, то можно воспользоваться следующим фактом:

Если на некотором интервале функция имеет единственную точку экстремума и эта точка является точкой максимума (минимума), то значение функции в этой точке будет наибольшим (наименьшим) на всем интервале.

Сформулируем достаточные условия экстремума функции:

Если при переходе через критическую точку производная функции меняет знак с плюса на минус (с минуса на плюс), то эта точка является точкой максимума (минимума) функции. (Предполагается, что функция определена и непрерывна в окрестности данной точки.)

Задача.

Прямоугольный участок огорожен с трех сторон забором периметра 4p. При каких размерах сторон площадь участка S будет наибольшей.

Решение.

Обозначим через и длины сторон прямоугольника.

Тогда S= . Параметры и не являются независимыми, а связаны соотношением (длина забора) +2 =4p. Отсюда: =4p-2 . Следовательно, функцию S можно представить как функцию одного параметра : S= (4p-2 ) .

Из условия задачи ясно, что параметр может изменяться на следующем отрезке 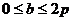. То есть задача сводится к отысканию наибольшего значения функции S=S( )= (4p-2 ) на отрезке .

Найдем производную: . Приравнивая ее нулю, получаем =p. Найденная точка лежит на отрезке .

Вычисляем S(0)=0, S(2p)=0, 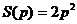- это значение и является наибольшим. Тогда размеры сторон равны: a=2p, b=p.

Задача.

Объем цилиндрической цистерны равен V. При каких размерах площадь ее полной поверхности будет наименьшей.

Решение.

Цилиндрическая цистерна характеризуется двумя параметрами: радиусом основания R и высотой H. Площадь полной поверхности выражается формулой S=2p +2pRH. Параметры R и H не являются независимыми (известен объем), а связаны соотношением V=p H. Отсюда H= . Подставляя Н в выражение для площади полной поверхности, получим S как функцию одной переменной S(R)= 2p + 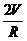. Возможная область изменения параметра R интервал (0;¥).

Найдем производную: 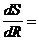4pR- 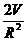. Приравнивая ее нулю, получаем R= 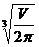. Заметим что: 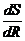<0 при R< 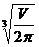, 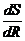>0 при R> 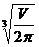. Поскольку при переходе через данную критическую точку производная меняет знак с минуса на плюс, то эта точка является точкой минимума. Поскольку на интервале (0;¥) данная точка является единственной точкой экстремума, то значение функции в этой точке будет наименьшим. 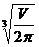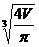Получаем, что цистерна имеет наименьшую полную поверхность при R= , H= =2R.

Заметим, что отношение H к R равно 2:

.

Итак, у цилиндра данного объёма с наименьшей полной поверхностью диаметр должен быть равен высоте.

Задача.

На странице книги печатный текст (вместе с промежутками между строками) должен занимать . Верхнее и нижнее поля должны быть по , правое и левое – по 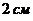. Каковы должны быть размеры страницы для того, чтобы ее площадь была наименьшей?

Решение.

Исследуемая величина, для которой нам предлагается отыскать наименьшее значение, есть площадь печатной страницы. Обозначим ширину печатного текста через 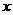, а длину - через 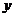. Площадь всей страницы можно найти по формуле: S=(x+4)(y+6), S=xy+6x+4y+24.

Таким образом, мы выразили функцию, для которой необходимо найти наименьшее значение, как функцию двух переменных. Используем данную в условии задачи площадь печатного текста: 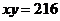, тогда 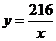. Выразим площадь страницы как функцию переменной :

.

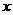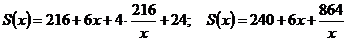Из условия задачи вытекают естественные ограничения на значения переменной 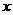: 0<x<¥. Таким образом, мы решаем задачу о нахождении наименьшего значения функции на заданном интервале. Найдем критические точки производной, приравняв ее нулю:

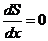при .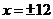

В соответствии с ограничениями, наложенными на 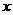, рас­сматриваем критическую точку 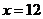, принадлежащую заданному интервалу. Определим, с помощью достаточного условия экстремума, будет ли найденная точка точкой локального максимума функции. Для этого проверим знак производной в окрестности точки .

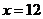При x<12 имеем 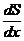<0, при x>12 имеем 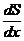>0. Данная точка является точкой минимума. Поскольку эта точка является единственной критической точкой интервале, то значение в этой точке будет наименьшим.

Таким образом, площадь печатной страницы будет наименьшей, если ее длина равна 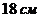, а ширина .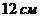