Геометрические приложения определенного интеграла

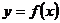Пусть функция неотрицательна и непрерывна на отрезке [а, b]. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой на [а, b] численно равна определенному интегралу , т.е.

Пример.Найдем площадь фигуры, ограниченной линиями ,

Решение. Из рис. 11 видно, что искомая площадь S криволинейного треугольника ОАВ равна разности двух площадей:

, '

каждая из которых находится по геометрическому смыслу определенного интеграла.

Рис. 11

Решая систему , получаем, что точка В пересечения прямой и кривой имеет координаты (2; 4). Тогда . Для вычисления второго интеграла определим вид подынтегральной функции, выразив из переменную у: .

Тогда получим:

Окончательно (ед.² ).

Ответ: ед².

Вопросы для самоконтроля

1. Что такое определенный интеграл?

2. Сформулируйте основные свойства определенного интеграла.

3. В чем заключается формула Ньютона-Лейбница для вычисления определенного интеграла?

4. Какие вы знаете способы вычисления определенных интегралов?

5. В чем заключается геометрический смысл определенного интеграла?

Контрольное задание

1. Вычислить интегралы:

_________________________________________________________________________________________________________________________________________________________

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

1. Вычислить площадь фигуры, ограниченной линиями:

y = , y = 0, x = 1 и x =5.

_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Раздел 4. Ряды

В результате изучения раздела студент должен:

знать:

¾ определение числового ряда, остатка ряда, свойства рядов;

¾ необходимый и достаточные признаки сходимости рядом с положительными членами: признак сравнения, признак Даламбера;

¾ определение знакочередующихся рядов, признак Лейбница;

¾ определение абсолютной и условной сходимости произвольных числовых рядов;

уметь:

¾ по формуле n-го члена записывать числовой ряд;

¾ записывать формулу n-го члена числового ряда;

¾ исследовать на сходимость положительные ряды;

¾ исследовать на абсолютную и условную сходимость числовые ря­ды.

Основные понятия

Числовым рядом называется сумма вида

Где числа u₁, u₂, u₃, …. , u_n, … называемые членами ряда, образуют бесконечную последовательность; член u_n называют общим членом ряда.

Пример. Записать ряд по его заданному общему члену: 1) .

Решение. Придавая n значения 1, 2, 3, …, имеем бесконечную последовательность чисел: ; ; ; …. , .Сложив её члены, получим ряд

Пример.Записать ряд по его заданному общему члену:

Решение.

Придавая n значения 1, 2, 3, … и учитывая, что 1! = 1, , 3! = 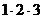…, получим ряд

Задание.Записать ряд по его заданному общему члену:

Решение.

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Ответ:

Пример. Найти n-й член ряда по его данным первым членам:

Решение: Знаменатели членов ряда, начиная с третьего, являются нечётными числами; следовательно, n-й член ряда имеет вид

Пример. Найти n-й член ряда по его данным первым членам:

Решение. Числители членов ряда представляют собой квадратные корни из натуральных чисел, а их соответствующие знаменатели равны n!. Знаки чередуются по закону(-1)ⁿ . Общий член ряда имеет вид

Задание.Найти n-й член ряда по его данным первым членам:

Решение.

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Ответ:

Суммы:

. . . . . . . . . . .

составленные из первых членов ряда, называются частичными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм S₁, S₂, S₃,…., S_n Если при бесконечном возрастании номера n частичная сумма ряда S_n стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.

или

Эта запись равносильна записи

Если частичная сумма S_n ряда при неограниченном возрастании n не имеет конечного предела ( в частности, стремится к +х или к – бесконечность), то такой ряд называют расходящимся.

Если ряд сходится, то значение S_n при достаточно большом n является приближенным выражением суммы ряда S.

Разность r_n = S - S_n называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. , и наоборот, если остаток стремится к нулю, то ряд сходится.

Пример.

Найти сумму членов ряда

Решение.

Находим частичные суммы членов ряда:

^; ; ;

Запишем последовательность частичных сумм: .

Общий член этой последовательности есть . Следовательно,

Последовательность частичных сумм имеет предел, равный . Итак, ряд сходится и его сумма равна .

Геометрический ряд. Рассмотрим несколько случаев нахождения частичной суммы первых n членов ряда , образованного из членов геометрической прогрессии.

1) . Для нахождения частичной суммы S_n воспользуемся формулой суммы членов убывающей геометрической прогрессии:

где a₁ – первый член, a_n=a₁q^n-1 – n –ый член, q – знаменатель прогрессии.

Следовательно

Находим сумму ряда:

Поскольку первое слагаемое под знаком предела является постоянным, а второе – бесконечно малой величиной (qⁿ->0 при n-> ). Таким образом, в данном случае ряд сходится, а его сумма есть .

2) . Частичную сумму S_n найдём по формуле суммы членов возрастающей геометрической прогрессии:

Тогда сумма ряда

Так как первое слагаемое под знаком предела есть бесконечно большая величина ( при ). В этом случае ряд расходится.

3) q=1. Находим

Следовательно . Значит, в данном случае ряд расходится.

4) q = -1. Имеем.

S₁ = a

S₂ = a – a =0

S₃ = a – a + a = a

S₄ = a – a + a – a = 0

. . . . . . . . . . . . . .

Т.е. S_n=0 при n четном и S_n= a при n нечётном. Отсюда следует, что последовательность частичных сумм не имеет предела и, значит, ряд расходится.

Итак, данный ряд сходится при и расходится при . Ряд вида будем называть геометрическим рядом.

Гармонический ряд. Ряд вида

называется гармоническим.

Запишем частичную сумму этого ряда:

Сумма S_n больше суммы представленной следующим образцом:

Или

Если , то

, или .

Следовательно, если , то , т.е. гармонический ряд расходится.