Характеристики временных рядов. Выявление тренда в динамических рядах экономических показателей.
Методы математической статистики широко применяются для анализа экономических временных рядов.
В общем случае временной ряд содержит детерминированную и случайную составляющие:
уt=f(t,хt)+et, t=1,…,Т,
где уt– значения временного ряда; f(t,хt) – детерминированная составляющая; хt – значения факторов, влияющих на детерминированную составляющую в момент t; et – случайная составляющая; Т – длина ряда.
Получив оценки детерминированной и случайной составляющих, решают задачи прогноза будущих значений, как самого временного ряда, так и его составляющих.
Если детерминированная составляющая зависит только от времени и линейна относительно своих параметров, то задача сводится к задаче множественной линейной регрессии, рассмотренной выше.
Действительно, в этом случае
уt=a0+a1j 1(t) +a2j 2(t) +…+amjm(t)+et, t=1,…,Т. (6.1)
В частном случае,
уt=a0+a1t1 +a2t2 +…+amtm+ et, t=1,…,Т. (6.2)
Детерминированная составляющая(называемаятрендом), в свою очередь представляется тремя составляющими.
Долговременная эволюторно изменяющаяся составляющая является результатом действия факторов, приводящих к постепенному изменению экономического показателя. Так, в результате научно-технического прогресса, совершенствования системы управления производством показатели эффективности производства растут, а удельные расходы на единицу полезного эффекта снижаются.
Долговременная циклическая составляющая проявляется на протяжении длительного времени в результате действия факторов, обладающих большим последействием или циклически изменяющихся во времени. Например, кризисы перепроизводства или периодичность солнечной активности, влияющая на урожайность.
Сезонная циклическая составляющая легко просматривается в колебаниях продуктивности сельскохозяйственных животных, а также в колебаниях розничного товарооборота в зависимости от времени года.
Эволюторно изменяющуюся долговременную составляющую во многих практических случаях представляют в виде некоторой аналитической функции (см. ниже), тогда как долговременная и сезонная циклические составляющие представляются периодическими функциями.
Для построения эволюторных трендов (моделирования тенденции) чаще всего применяются те же функции, которые мы рассматривали выше:
- линейный тренд: ŷt=b+at;
- гипербола: ŷt= b+a/t;
- экспоненциальный тренд: ŷt= е b+at (или ŷt=bat);
- тренд в форме степенной функции ŷt= bta;
- полином порядка m: ŷt= b + a1t + a2t2 +…+ amtm.
Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t. Для нелинейных трендов предварительно проводят процедуру их линеаризации.
Пример 6.1. Имеются помесячные данные о темпах роста заработной платы в РФ за 10 месяцев 2008 г. в процентах к уровню декабря 2007г. (табл. 6.1). Требуется выбрать наилучший тип тренда и определить его параметры.
Таблица 6.1
| месяц | ||||||||||
| Темп роста з/платы | 82,3 | 87,3 | 99,4 | 104,8 | 107,2 | 121,6 | 118,6 | 114,1 | 123,0 | 127,3 |
Определим параметры основных видов тренда. Результаты этих расчетов представлены в табл. 6.2.
Таблица 6.2
| Тип тренда | уравнение | R2 |
| Линейный | ŷt= 82,66 + 4,72t | 0,887 |
| Парабола | ŷt= 72,9 + 9,599t – 0,444t2 | 0,937 |
| Степенной | lnŷt= 4,39 + 0,193lnt | 0.939 |
| Экспоненциальный | lnŷt= 4.43 + 0.045t | 0.872 |
| Гиперболический | ŷt= 122.57 – 47.63/t | 0.758 |
Наилучшей является степенная форма тренда, которая в исходном виде (после потенцирования) примет следующий вид
ŷt= е4.39t0,193
или ŷt= 80,32t0,193.
Наиболее простую экономическую интерпретацию имеют параметры линейного и экспоненциального трендов.
Параметры линейного тренда можно интерпретировать так:
b – начальный уровень временного ряда при t=0;
a – средний за период абсолютный прирост ряда.
Применительно к вышеприведенному примеру можно сказать, что темпы роста месячной заработной платы за 10 месяцев 2008г. изменялись от 82,66% со средним за месяц абсолютным приростом 4,72%.
Параметры экспоненциального тренда имеют следующую интерпретацию:
b – начальный уровень временного ряда при t=0;
еa– средний за период коэффициент роста ряда.
В примере уравнение экспоненциального тренда в исходной форме имеет вид
ŷt= е4.43е0,045t
или ŷt= 83,96е0,045t.
Следовательно, можно сказать, что темпы роста месячной заработной платы за 10 месяцев 2004г. изменялись от 83,96% со средним за месяц темпом роста, равным е0,045= 1,046.
Выбранная прогнозная эмпирическая функция, описывающая динамический ряд, должна минимизировать стандартное отклонение S на интервале оценивания, обеспечивать тесноту связи (по коэффициенту корреляции); аппроксимирующее уравнение должно быть адекватно фактической временной тенденции (по F-критерию) и устранять автокорреляцию.
Технология моделирования на основе тренда включает следующие этапы.
1.Анализ и обработка исходной информации.
2.Выбор вида функции, описывающей временной ряд.
3.Расчет параметров функции (например, методом наименьших квадратов).
4.Оценка адекватности и достоверности уравнения тренда.
Оценка адекватности проводится с помощью показателей, рассмотренных в теме 2, так как трендовые модели являются частным случаем регрессионных моделей. Следует отметить, что временные ряды качественно отличаются от простых числовых выборок, поэтому обычно в целях проверки адекватности модели используют оценку устойчивости тенденции временного ряда.
Определение устойчивости изменения показателей временного ряда
Устойчивость характеризуется преобладанием закономерности над случайностью в изменении уровней ряда. Устойчивость экономических процессов можно рассматривать как категорию противоположную колеблемости, и как устойчивость направленности изменений.
В первом случае показатель устойчивости можно измерять как разность между единицей и относительным показателем колеблемости. В свою очередь показатель колеблемости вычисляется как отношение среднеквадратического отклонения от тренда к среднему значению показателя.
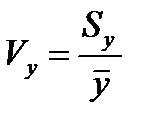, где 
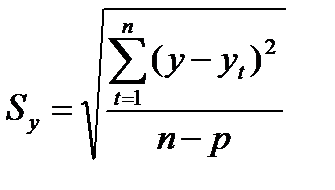
- показатель колеблемости уровней временного ряда;
- среднеквадратическое отклонение уровней временного ряда от рассчитанных по уравнению тренда (стандартное отклонение);
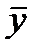- среднее значение уровней временного ряда;
- фактические значения уровней временного ряда;
- значения уровней временного ряда, рассчитанные по уравнению тренда.
Следовательно, показатель устойчивости будет равен: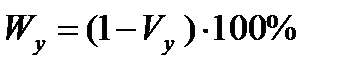 
Показатель устойчивости характеризует близость фактических уровней к тренду. Изменения показателей считаются устойчивыми, если показатель устойчивости не менее 67% (то есть показатель колеблемости не превышает 33%).
Во втором случае устойчивость характеризует уровни временного ряда как процесс их направленного изменения. С этих позиций полной устойчивостью направленного изменения уровней временного ряда следует считать такое их изменение, в процессе которого каждый следующий уровень либо выше всех предшествующих (устойчивый рост), либо ниже всех предшествующих (устойчивое снижение). Всякое нарушение строго ранжированной последовательности уровней свидетельствует о неполной устойчивости их развития.
При такой интерпретации в качестве показателя устойчивости тенденции можно использовать коэффициент корреляции рангов Ч.Спирмена:
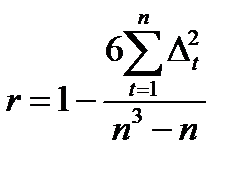, где
n – число уровней временного ряда;
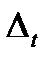- разность рангов уровней и номеров периодов времени.
Коэффициент корреляции рангов Спирмена изменяется от -1 до 1. При хаотическом чередовании подъемов и падений исследуемого процесса его значение буде близко к нулю. Значение коэффициента близкое к 1 доказывает устойчивость тенденции возрастания, близость коэффициента к -1 свидетельствует об устойчивой тенденции убывания.