Прогнозирование.Доверительный интервал прогноза.
Расчеты и проверка достоверности полученных оценок коэффициентов регрессии не являются самоцелью, это лишь необходимый промежуточный этап. Основное – это использование модели для анализа и прогноза поведения изучаемого экономического явления. Прогноз осуществляется подстановкой значения фактора х в полученную формулу регрессии.
Используем полученное в примере 2.1 уравнение регрессии для прогноза объема товарооборота. Пусть намечается открытие магазина с численностью работников х=140 чел., тогда достаточно обоснованный объем товарооборота следует установить по уравнению ŷ(х)= –0,974 + 0,01924×140=1,72 млрд. руб.
Доверительный интервал для прогностического значения у(х)= a0+a1хопределяется по формуле
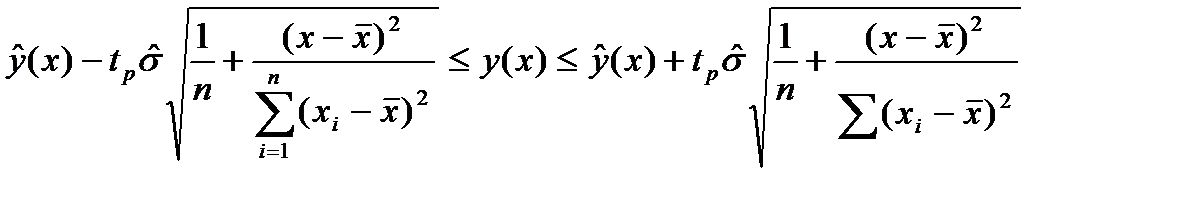, (5.2)
где tp – критическая граница распределения Стьюдента с n – 2 степенями свободы, соответствующая уровню значимости р. Для получения доверительного интервала воспользуемся выражением (5.2).
Выберем уровень значимости 5%. Число степеней свободы у нас 8 – 2 = 6, тогда по таблице распределения Стьюдента (приложение 1) находим
t0.05(6)=2,447.s=Ö 0,008=0,089,
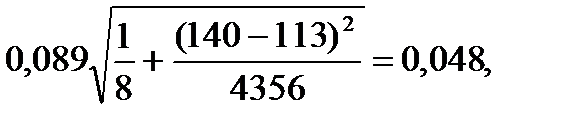
следовательно, с вероятностью 95% истинные значения объемов товарооборота будут лежать в пределах
1,72 – 2,447×0,048<y(x)<1,72+2,447×0,048, или 1,60<y(x)<1,84.
5.8. Практический блок
Пример.Построить модель связи между указанными факторами, проверить её адекватность, осуществить точечный и интервальный прогноз методом экстраполяции.
1. Построить диаграмму рассеяния в EXCELи сделать предварительное заключение о наличии связи.
Таблица 5.6Диаграмма 5.1
| x | Y |
| 2,1 | 29,5 |
| 2,9 | 34,2 |
| 3,3 | 30,6 |
| 3,8 | 35,2 |
| 4,2 | 40,7 |
| 3,9 | 44,5 |
| 5,0 | 47,2 |
| 4,9 | 55,2 |
| 6,3 | 51,8 |
| 5,8 | 56,7 |
Вывод: Из диаграммы 5.1 видно, что связь между факторами x и y
прямая сильная линейная связь.
2. Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами х и у.
Таблица 5.7
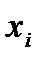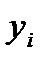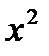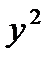| № |  |  |  |  | xy |  |  |  |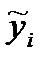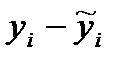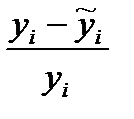
| 2,1 | 29,5 | 4,41 | 870,25 | 61,95 | 27,91 | 1,59 | 0,054 | |
| 2,9 | 34,2 | 8,41 | 1169,64 | 99,18 | 33,46 | 0,74 | 0,022 | |
| 3,3 | 30,6 | 10,89 | 936,36 | 100,98 | 36,23 | -5,63 | 0,184 | |
| 3,8 | 35,2 | 14,44 | 1239,04 | 133,76 | 39,69 | -4,49 | 0,128 | |
| 4,2 | 40,7 | 17,64 | 1656,49 | 170,94 | 42,47 | -1,77 | 0,043 | |
| 3,9 | 44,5 | 15,21 | 1980,25 | 173,55 | 40,39 | 4,11 | 0,092 | |
| 5,0 | 47,2 | 2227,84 | 48,01 | -0,81 | 0,017 | |||
| 4,9 | 55,2 | 24,01 | 3047,04 | 270,48 | 47,32 | 7,88 | 0,143 | |
| 6,3 | 51,8 | 39,69 | 2683,24 | 326,34 | 57,02 | -5,22 | 0,101 | |
| 5,8 | 56,7 | 33,64 | 3214,89 | 328,86 | 53,55 | 3,15 | 0,056 | |
| ИТОГО: | 42,2 | 193,34 | 19025,04 | 1902,04 | 0,840 | |||
| Среднее зн. | 4,22 | 42,56 | 19,334 | 1902,504 | 190,204 |
2.1.Проверим тесноту связи между факторами:
; 
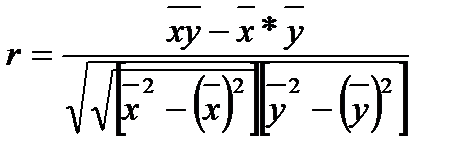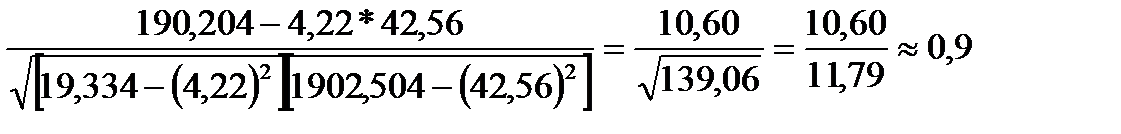
Вывод: связь сильная.
2.2.Проверим статистическую значимость по критерию Стьюдента:
1)Критерий Стьюдента: tвыб<=tкр
2)Но: r=0 tкр=2,31
tвыб=rвыб*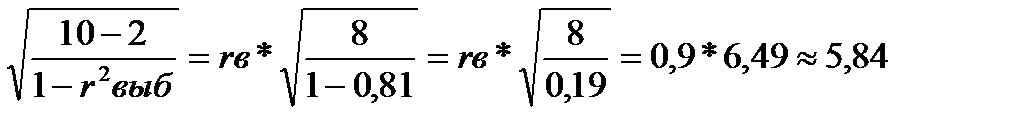 
Вывод: таким образом поскольку tвыб=5,84<tкр=2,31, то с доверительной вероятностью
90% нулевая гипотеза отвергается, это указывает на наличие сильной линейной связи.
3. Полагая, что связь между факторами х и у может быть описана линейной функцией, используя процедуру метода наименьших квадратов, запишите систему нормальных уравнений относительно коэффициентов линейного уравнения регрессии. Любым способом рассчитайте эти коэффициенты.
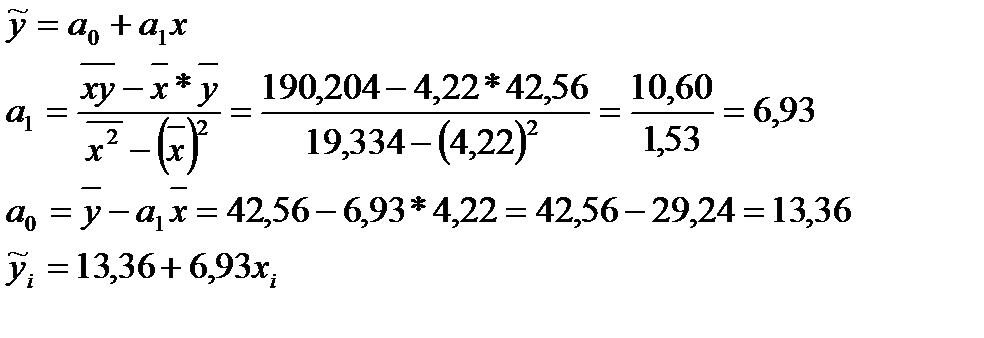
Последовательно подставляя в уравнение регрессии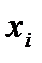 
из графы (2) табл.5.7, рассчитаем значения и заполним графу (7) табл.5.7.
4. Для полученной модели связи между факторами Х и У рассчитайте среднюю ошибку аппроксимации. Сделайте предварительное заключение приемлемости полученной модели.
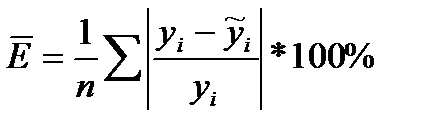
Для расчета заполним 8-ую и 9-ую графу табл.5.7.
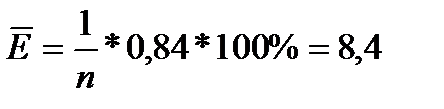<Екр=12%
Вывод: модель следует признать удовлетворительной.
5. Проверьте значимость коэффициента уравнения регрессии a1 на основе t-критерия Стьюдента.
Решение: Таблица 5.8
| № |  |  |  |  |  |  |
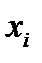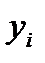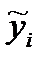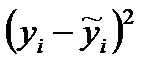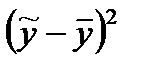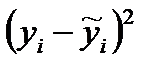| 2,1 | 29,5 | 27,91 | 2,5281 | 214,623 | 170,5636 | |
| 2,9 | 34,2 | 33,46 | 0,5476 | 82,81 | 69,8896 | |
| 3,3 | 30,6 | 36,23 | 31,6969 | 40,069 | 143,0416 | |
| 3,8 | 35,2 | 39,69 | 20,1601 | 8,237 | 54,1696 | |
| 4,2 | 40,7 | 42,47 | 3,1329 | 0,008 | 3,4596 | |
| 3,9 | 44,5 | 40,39 | 16,8921 | 4,709 | 3,7636 | |
| 47,2 | 48,01 | 0,6561 | 29,703 | 21,5296 | ||
| 4,9 | 55,2 | 47,32 | 62,0944 | 22,658 | 159,7696 | |
| 6,3 | 51,8 | 57,02 | 27,2484 | 209,092 | 85,3776 | |
| 5,8 | 56,7 | 53,55 | 9,9225 | 120,78 | 199,9396 | |
| ИТОГО: | 42,2 | 425,6 | 426,1 | 174,8791 | 732,687 | 911,504 |
| Среднее | 4,22 | 42,56 |
Статистическая проверка:
Вывод: С доверительной вероятностью 90% коэффициент a1- статистически значим, т.е. нулевая гипотеза отвергается.
6. Проверьте адекватность модели (уравнения регрессии) в целом на основе F-критерия Фишера-Снедекора.
Решение:
Процедура статистической проверки:
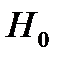:модель не адекватна
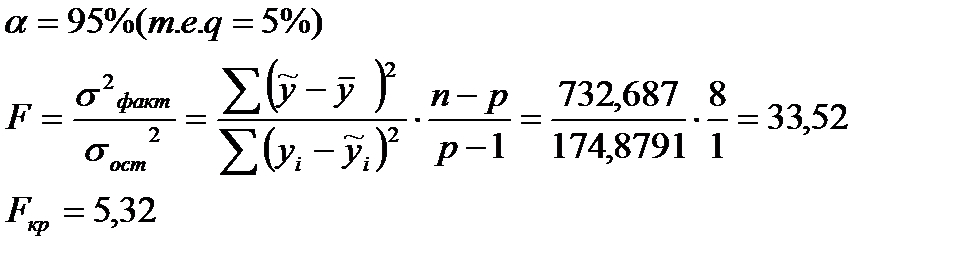
Вывод: т.к. Fвыб.>Fкр., то с доверительной вероятностью 95% нулевая гипотеза отвергается (т.е. принимается альтернативная). Изучаемая модель адекватна и может быть использована для прогнозирования и принятия управленческих решений.
7. Рассчитайте эмпирический коэффициент детерминации.
Решение:
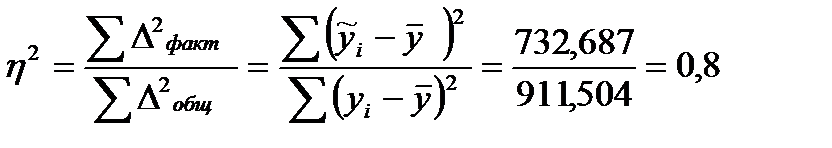(таб. 3)
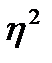-показывает долю вариации.
Вывод: т.е. 80% вариации объясняется фактором, включенным в модель, а 20% не включенными в модель факторами.
8. Рассчитайте корреляционное отношение. Сравните полученное значение с величиной линейного коэффициента корреляции.
Решение:
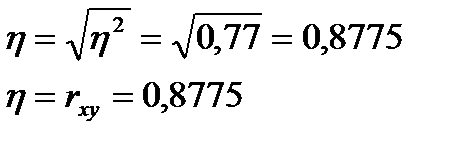
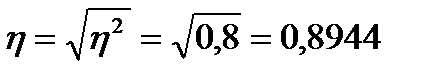
Эмпирическое корреляционное отношение указывает на тесноту связи между двумя факторами для любой связи, если связь линейная, то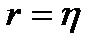 
, т.е. коэффициент корреляции совпадает с коэффициентом детерминации.
9. Выполните точечный прогноз для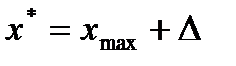 
.
Решение:
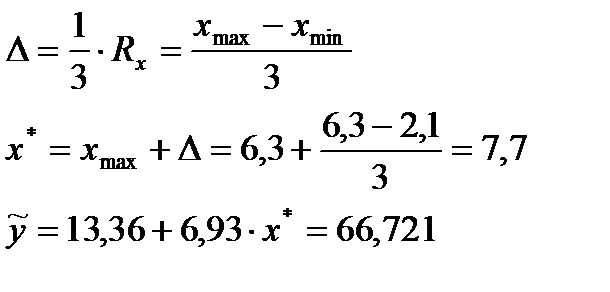
10-12. Рассчитайте доверительные интервалы для уравнения регрессии и для результирующего признака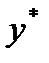 
при доверительной вероятности 
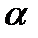=90%. Изобразите в одной системе координат:
а) исходные данные,
б) линию регрессии,
в) точечный прогноз,
г) 90% доверительные интервалы.
Сформулируйте общий вывод относительно полученной модели.
Решение:
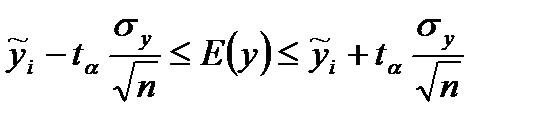-математическое ожидание среднего.
Для выполнения интервального прогноза рассматриваем две области.
1) для y из области изменения фактора x доверительные границы для линейного уравнения регрессии рассчитывается по формуле:
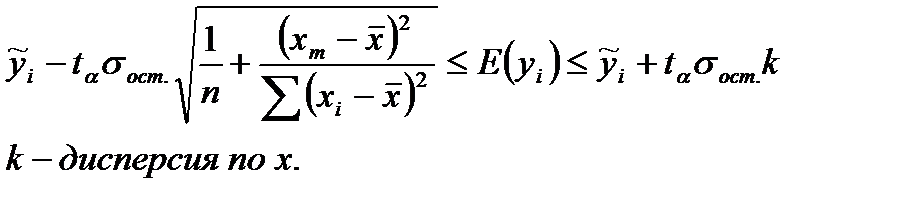
2) для прогнозного значения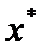 
доверительный интервал для 
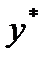рассчитывается по формуле:
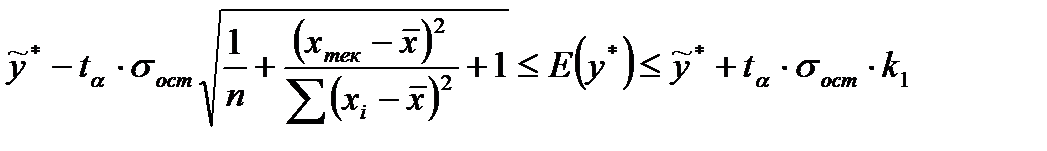
Исходные данные:
1) n=10
2) t=2,31(таб.)
3) 
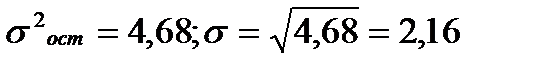
4) 
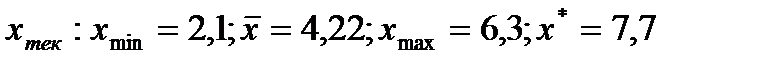
5) 
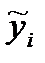: 27,91 42,56 57,02 66,72
6) 
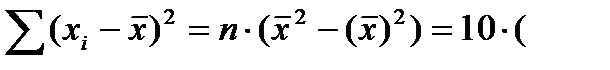19,334-4,222)=1,53.
Таблица 5.9
| № | |||||||||||
| 1 | 2,1 | -2,12 | 4,49 | 3,03 | 1,74 | 2,31 | 4,68 | 18,81 | 27,91 | 9,10 | 46,72 |
| 4,22 | 0,00 | 0,00 | 0,1 | 0,32 | 2,31 | 4,68 | 3,46 | 42,56 | 39,10 | 46,02 | |
| 6,3 | 2,08 | 4,33 | 2,93 | 1,71 | 2,31 | 4,68 | 18,49 | 57,02 | 38,53 | 75,51 | |
| 7,7 | 3,48 | 12,11 | 9,02 | 2,31 | 4,68 | 32,43 | 66,72 | 34,29 | 99,15 |
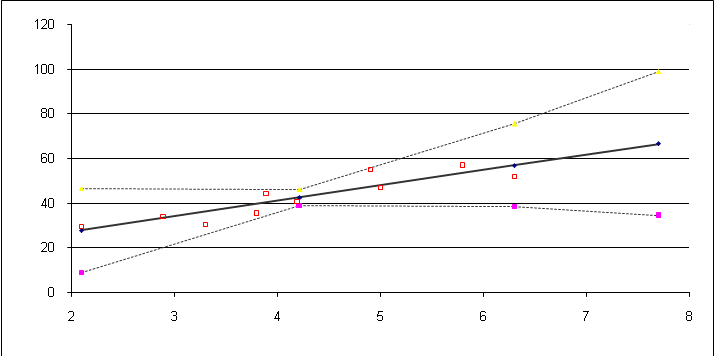
Вывод: поскольку 90% точек наблюдения попало в 90% доверительный интервал, данная модель и ее доверительные границы могут использоваться для прогнозирования с 90% доверительной вероятностью.
Контрольные вопросы
1. Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками.
2. Виды автокорреляции и их краткая характеристика.
3. Автокорреляция в остатках и порядок её обнаружения.
4. Виды автокорреляции в остатках.
5. Порядок использования критерия Дарбина-Уотсона.
6. Автокорреляция в исходных данных и порядок определения её наличия.
7. Методы устранения влияния автокорреляции на результаты прогнозирования.
8. Обобщенный метод наименьших квадратов (ОМНК).
9. Что понимается под гомоскедастичностью?
10. Как проверяется гипотеза о гомоскедастичности ряда остатков?
11. Оценка качества регрессии. Проверка адекватности и достоверности модели.
12. Значимость коэффициентов регрессии (критерий Стъюдента).
13. Дисперсионный анализ. Проверка достоверности модели связи (по F-критерию Фишера).
14. Коэффициенты и индексы корреляции. Мультиколлениарность.
15. Оценка значимости корреляции. Детерминация.
16. Средняя ошибка аппроксимации.
17. Принятие решений на основе уравнений регрессии.
18. В каких задачах эконометрики используется распределение Фишера?
19. Таблицы каких распределений используются при оценке качества линейной регрессии?
20. Каковы особенности практического применения регрессионных моделей?
21. Как осуществляется прогнозирование экономических показателей с использованием моделей линейной регрессии?
22. Как можно оценить «естественный» уровень безработицы с использованием модели линейной регрессии?
23. В каких случаях необходимо уточнение линейной регрессионной модели и как оно осуществляется?
24. Когда необходимо выведение из рассмотрения незначимых объясняющих переменных и добавление новых переменных?
Задания и задачи
1. Имеются данные о деятельности крупнейших компаний США в 2006г.
| № п/п | Чистый доход, млрд долл.США, у | Оборот капитала, млрд долл. США, х1 | Использованный капитал, млрд долл. США, х2 | Численность служащих, тыс.чел., х3 | Рыночная капитализация компании, млрд долл. США, х4 |
| 0,9 | 31,3 | 18,9 | 43,0 | 40,9 | |
| 1,7 | 13,4 | 13,7 | 64,7 | 40,5 | |
| 0,7 | 4,5 | 18,5 | 24,0 | 38,9 | |
| 1,7 | 10,0 | 4,8 | 50,2 | 38,5 | |
| 2,6 | 20,0 | 21,8 | 106,0 | 37,3 | |
| 1,3 | 15,0 | 5,8 | 96,6 | 26,5 | |
| 4,1 | 137,1 | 99,0 | 347,0 | 37,0 | |
| 1,6 | 17,9 | 20,1 | 85,6 | 36,8 | |
| 6,9 | 165,4 | 60,6 | 745,0 | 36,3 | |
| 0,4 | 2,0 | 1,4 | 4,1 | 35,3 | |
| 1,3 | 6,8 | 8,0 | 26,8 | 35,3 | |
| 1,9 | 27,1 | 18,9 | 42,7 | 35,0 | |
| 1,9 | 13,4 | 13,2 | 61,8 | 26,2 | |
| 1,4 | 9,8 | 12,6 | 212,0 | 33,1 | |
| 0,4 | 19,5 | 12,2 | 105,0 | 32,7 | |
| 0,8 | 6,8 | 3,2 | 33,5 | 32,1 | |
| 1,8 | 27,0 | 13,0 | 142,0 | 30,5 | |
| 0,9 | 12,4 | 6,9 | 96,0 | 29,8 | |
| 1,1 | 17,7 | 15,0 | 140,0 | 25,4 | |
| 1,9 | 12,7 | 11,9 | 59,3 | 29,3 | |
| -0,9 | 21,4 | 1,6 | 131,0 | 29,2 | |
| 1,3 | 13,5 | 8,6 | 70,7 | 29,2 | |
| 2,0 | 13,4 | 11,5 | 65,4 | 29,1 | |
| 0,6 | 4,2 | 1,9 | 23,1 | 27,9 | |
| 0,7 | 15,5 | 5.8 | 80,8 | 27,2 |
Задание:
Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов.
Дайте сравнительную оценку силы связи факторов с результатом с помощью коэффициентов эластичности.
Рассчитайте матрицы парных коэффициентов корреляции и на их основе отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.
Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
Рассчитайте ошибки и доверительный интервал прогноза для
уровня значимости 5 или 10% (γ = 0,05; γ = 0,10).
2. Имеются данные о деятельности крупнейших компаний США в 2006г.
| № п/п | Чистый доход, млрддолл. у | Оборот капитала, млрддолл. США, х1 | Использованный капитал, млрддолл. х2 | Численность, тыс. чел., х3 |
| 6,6 | 6,9 | 83,6 | 222,0 | |
| 3,0 | 18.0 | 6,5 | 32,0 | |
| 6,5 | 107,9 | 50,4 | 82,0 | |
| 3,3 | 16,7 | 15,4 | 45,2 | |
| 0,1 | 79,6 | 29,6 | 299,3 | |
| 3,6 | 16,2 | 13,3 | 41,6 | |
| 1,5 | 5,9 | 5,9 | 17,8 | |
| 5,5 | 53,1 | 27,1 | 151,0 | |
| 2,4 | 18,8 | 11,2 | 82,3 | |
| 3,0 | 35,3 | 16,4 | 103,0 | |
| 4,2 | 71,9 | 32,5 | 225,4 | |
| 2,7 | 93,6 | 25,4 | 675,0 | |
| 1,6 | 10,0 | 6,4 | 43,8 | |
| 2,4 | 31,5 | 12,5 | 102,3 | |
| 3,3 | 36,7 | 14,3 | 105,0 | |
| 1,8 | 13,8 | 6,5 | 49,1 | |
| 2,4 | 64,8 | 22,7 | 50,4 | |
| 1,6 | 30,4 | 15,8 | 480,0 | |
| 1,4 | 12,1 | 9,3 | 71,0 | |
| 0,9 | 31,3 | 18,9 | 43,0 |
Задание:
Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов.
Дайте сравнительную оценку силы связи факторов с результатом с помощью коэффициентов эластичности.
Рассчитайте матрицы парных и частных коэффициентов корреляции и на их основе отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.
Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (α = 0,05; α = 0,10).
Оцените полученные результаты, выводы оформите в аналитической записке.