Полная и приведённая системы вычетов

ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

6. 1. Определение 1.

Классом чисел по данному модулю т называется множество всех тех и только тех целых чисел, которые при делении на т имеют один и тот же остаток r, то есть сравнимых по модулю т (т ÎN, т > 1).

Обозначение класса чисел, имеющих остаток r: .

Каждое число из класса называется вычетом по модулю т, а сам класс называется классом вычетов по модулю т.

6. 2. Свойства множества классов вычетов по модулю т:

1) всего по модулю т будет т классоввычетов: Z_т = { , , , … , };

2) каждый класс содержит бесконечное множество целых чисел (вычетов) вида: = {a = mq + r / qÎZ, 0£ r < m}

3) "а Î : а º r (mod m);

4) "а, b Î : а º b (mod m), то есть любые два вычета, взятые из одного класса, сравнимы по модулю т;

5) "а Î , "b Î : а b (mod m), то есть никакие два вычета; взятые из разных классов, несравнимы по модулю т.

6. 3. Определение 3.

Полной системой вычетов по данному модулю т называется любой набор т чисел, взятых по одному и только по одному из каждого класса вычетов по модулю т .

Пример: если m = 5, то {10, 6, – 3, 28, 44} – это полная система вычетов по модулю 5 (причём, не единственная !)

В частности,

множество {0, 1, 2, 3, … , m –1} – это система наименьших неотрицательных вычетов;

множество {1, 2, 3, … , m –1, т}– это система наименьших положительных вычетов.

6. 4. Отметим, что:

если {х₁, х₂, … , х_т} – полная система вычетов по модулю т, то

.

6. 5. Теорема 1.

Если {х₁, х₂, … , х_т} – полная система вычетов по модулю т, "а, b Î Z и (а, т) = 1, – то система чисел {ах₁ + b, ах₂ + b, … , ах_т+ b}также образует полную систему вычетов по модулю т .

6. 6. Теорема 2.

Все вычеты одного и того же класса вычетов по модулю т имеют с числом т один и тот же наибольший общий делитель: "а, b Î Þ (а; т) = (b; т).

6. 7. Определение 4.

Класс вычетов по данному модулю т называется взаимно простым с модулем т, если хотя бы один вычет этого класса – взаимно простой с т.

Заметим, что в этом случае по теореме 2 все числа этого класса будут взаимно простыми с модулем т.

6. 8. Определение 5.

Приведённой системой вычетов по данному модулю т называется система вычетов, взятых по одному и только по одному из каждого класса, взаимно простого с модулем т .

6. 9. Отметим, что:

1) приведённая система вычетов по модулю т содержит j(т) чисел {х₁, х₂,…, };

2) : .

3) " х_i : (х_i, m) = 1;

Пример: Пусть по модулю т = 10 имеется 10классоввычетов:

Z₁₀ = { , , , , , , , , , }– множество классоввычетов по модулю 10. Полная система вычетов по mod 10 будет, например, такая: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Множество классов вычетов, взаимно простых с модулем m=10: { , , , }(j(10) = 4).

Приведённая система вычетов по модулю10 будет, например,

{1, 3, 7, 9}, или {11, 43, – 5, 17}, или { – 9, 13, – 5, 77} и т.д. (везде j(10) = 4 числа).

6.10. Практически: чтобы составить одну из возможных приведённых систем вычетов по mod m , нужно из полной системы вычетов по mod m выбрать те вычеты, которые взаимно простые с т. Таких чисел будет j(т).

6.11. Теорема 3.

Если {х₁, х₂,…, } – приведённая система вычетов по модулю т и

(а, m) = 1, – то система чисел {ах₁, ах₂ , … , ах_j(т)} также образует

приведённую систему вычетов по модулю т .

6.12. Определение 6.

Суммой ( Å ) классов вычетов и по модулю т называется класс вычетов , то есть класс вычетов, состоящий из чисел а + b, равных сумме любых двух вычетов, взятых по одному из каждого данного класса и : Å = , где "а Î , "b Î .

6.13. Определение 7.

Произведением ( Ä ) классов вычетов и по модулю т называется класс вычетов , то есть класс вычетов, состоящий из чисел а ´ b, равных произведению любых двух вычетов, взятых по одному из каждого данного класса и : Ä = , где "а Î , "b Î .

Таким образом, в множестве классов вычетов по модулю т: Z_т = { , , ,…, } определены две алгебраические операции – "сложения" и "умножения".

6.14. Теорема 4.

Множество классов вычетов Z_т по модулю т является ассоциативно-коммутативным кольцом с единицей:

< Z_т , +, · > = < { , , ,…, }, +, · > – кольцо.

ТИПОВЫЕ ЗАДАЧИ

1. Составить по модулю т = 9:

1) полную систему наименьших положительных вычетов;

2) полную систему наименьших неотрицательных вычетов;

3) произвольную полную систему вычетов;

4) полную систему наименьших по абсолютной величине вычетов.

Ответ:1) {1, 2, 3, 4, 5, 6, 7, 8, 9}; 2) {0, 1, 2, 3, 4, 5, 6, 7, 8};

3) например, {10, – 7, 21, 49, – 4, 15, 25, – 1, 0}; 4) {– 4, – 3, – 2, – 1, 0, 1, 2, 3, 4}.

2. Составить приведённую систему вычетов по модулю т = 12.

Решение.

1) Составим полную систему наименьших положительных вычетов по модулю т = 12:

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} (всего т = 12 чисел).

2) Вычеркнем из этой системы числа, не взаимно простые с числом 12:

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.

3) Оставшиеся числа, взаимно простые с числом 12, образуют искомую приведённую систему вычетов по модулю т = 12 (всего j(т) = j(12) = 4 числа).

Ответ: {1, 5, 7, 11} – приведённая система вычетов по модулю т = 12.

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

130. Составьте 1) полную систему наименьших положительных вычетов; 2) полную систему наименьших неотрицательных вычетов; 3) произвольную систему вычетов; 4) полную систему наименьших по абсолютной величине вычетов; 5) приведённую систему вычетов: а) по модулю m = 6; б) по модулю m = 8.

131. Является ли множество {9, 2, 16, 20, 27, 39, 46, 85} полной системой вычетов по модулю 8 ?

132 По какому модулю множество{20, – 4, 22, 18, – 1}является полной системой вычетов?

133. Составьте приведённую систему вычетов по модулю m , если а) m = 9; б) m = 24; в) m = 7. Сколько чисел должна содержать такая система ?

134. Сформулируйте основные свойства полной системы вычетов и приведённой системы вычетов по модулю m .

135. Какими элементами отличаются приведённая и полная системы наименьших неотрицательных вычетов по простому модулю ?

136. При каком условии числа а и – а принадлежат одному классу вычетов по модулю m ?

137. Каким классам вычетов по модулю 8 принадлежат все простые числа р ³ 3 ?

138. Образует ли множество чисел {0, 2⁰, 2¹, 2², ... , 2⁹ } полную систему вычетов по модулю 11 ?

139. Скольким классам вычетов по модулю 21 принадлежат все вычеты из одного класса вычетов по модулю 7 ?

140. Множество целых чисел Z распределите по классам вычетов по модулю 5. Составьте таблицы сложения и умножения в образовавшемся множестве классов вычетов Z₅. Является ли множество Z₅: а) группой с операцией сложения классов ? б) группой с операцией умножения классов ?

§ 7. ТЕОРЕМА ЭЙЛЕРА. МАЛАЯ ТЕОРЕМА ФЕРМА

ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

7. 1. Теорема 1.

Если аÎZ, тÎN, т >1 и (а; т) = 1 , – то в бесконечной последовательности степеней а¹, а², а³, ... , а^s, … , а^t, … найдутся хотя бы две степени с показателями s и t (s < t) такие, что . (*)

7. 2. Замечание. Обозначив t – s = k > 0, из (*) получим: . Возводя обе части этого сравнения в степень nÎN , получим: (**). Это означает, что существует бесконечное множество степеней числа a, удовлетворяющих сравнению (**). Но как найти эти показатели? Каков наименьший показатель, удовлетворяющий сравнению (**) ? На первый вопрос отвечает теорема Эйлера (1707 – 1783).

7. 3. Теорема Эйлера.

Если аÎZ, тÎN, т >1 и (а; т) = 1, – то . (13)

Пример. Пусть а = 2, т = 21, (а; т) = (2; 21) = 1. Тогда . Так как j (21) = 12, то 2¹² º 1(mod 21). В самом деле: 2¹² = 4096 и (4096 – 1) 21. Тогда очевидно, что 2²⁴ º 1(mod 21), 2³⁶ º 1(mod 21) и так далее. Но является ли показатель степени 12 – наименьшим, удовлетворяющим сравнению 2ⁿ º 1(mod 21) ? Оказывается, нет. Наименьшим показателем будет п = 6: 2⁶ º 1(mod 21), ибо 2⁶ – 1 = 63, а 63 21. Заметим, что наименьший показатель следует искать только среди делителей числа j(т) (в данном примере – среди делителей числа j(21) = 12 ).

7. 4. Малая теорема Ферма (1601 – 1665).

Для любого простого числа р и любого числа аÎZ, не делящегося на р, имеет место сравнение . (14)

Пример. Пусть а = 3, р = 5, где 3 не 5. Тогда или .

7. 5. Обобщёння теорема Ферма.

Для любого простого числа р и произвольного числа аÎZ имеет место сравнение (15)

ТИПОВЫЕ ЗАДАЧИ

1. Докажите, что 38 ⁷³ º 3(mod 35).

Решение.

1) Так как (38; 35) = 1, то по теореме Эйлера ; j(35) = 24, значит,

(1).

2) Из сравнения (1) по следствию 2 свойства 5⁰ числовых сравнений имеем:

(2) .

3) Из сравнения (2) по следствию 1 свойства 5⁰ сравнений: 38⁷² ×38 º 1×38 (mod 35) Þ Þ38 ⁷³ º38 º 38–35 = 3(mod 35) Þ 38 ⁷³ º 3 (mod 35), что и требовалось доказать.

2. Дано: а = 4, т = 15. Найти наименьший показатель степени k, удовлетворяющий сравнению (*)

Решение.

1) Так как (a; m) = (4; 25) = 1, то по теореме Эйлера , j(25) = 20, поэтому .

2) Является ли найденный показатель степени – число 20 – наименьшим натуральным числом, удовлетворяющим сравнению (*)? Если существует показатель степени, меньший 20, то он должен быть делителем числа 20. Значит, искомый наименьший показатель k надо искать среди множества чисел n = {1, 2, 4, 5, 10, 20}– делителей числа 20.

3) При п = 1: ;

при п = 2: ;

при п = 3: (рассматривать не надо);

при п = 4: ;

при п = 5: ;

при п = 6, 7, 8, 9: (рассматривать не надо);

при п = 10: .

Итак, наименьшим показателем степени k, удовлетворяющим сравнению(*), является k= 10.

Ответ: .

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

141. По теореме Эйлера . При а = 3, т = 6 имеем: .

Так как j(6) = 2, то 3 ²º1(mod 6), или 9º1(mod 6), Тогда, по лемме, (9 – 1) 6 или 8 6 (нацело!?). Где ошибка?

142. Докажите, что: а) 23 ¹⁰⁰º1(mod 101); б) 81 ⁴⁰º 1(mod100); в) 2 ⁷³º 2 (mod 73).

143. Докажите, что а) 1¹⁶ + 3¹⁶ + 7¹⁶ + 9¹⁶ º 4 (mod 10);

б) 5 ^{4п + 1} + 7 ^{4п + 1} делится без остатка на 12..

144. Докажите теорему, обратную теореме Эйлера: если а ^{j (m)} º 1(mod m), то (а, m) =1.

145. Найдите наименьший показатель степени kÎN, удовлетворяющий данному сравнению: а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з) .

и) ; к) ; л) ; м) .

146. Найдите остаток от деления:

а) 7¹⁰⁰ на 11; б) 9⁹⁰⁰ на 5; в) 5¹⁷⁶ на 7; г) 2¹⁹⁹⁹ на 5; д) 8³⁷⁷ на 5;

е) 26 ⁵⁷ на 35; ж) 35 ³⁵⁹ на 22; з) 5⁷¹⁸ на 103; и) 27²⁶⁰ на 40; к) 25¹⁹⁹⁸ на 62.

147*. Докажите, что а ⁵⁶¹ º а (mod 11).

148*. Если каноническое разложение натурального числа п не содержит множителей 2 и 5, то 12-я степень этого числа оканчивается цифрой 1. Докажите.

149*. Докажите, что 2 ⁶⁴ º 16 (mod 360).

150*. Докажите: если (а, 65) =1 , (b, 65) =1, то a¹² – b¹² делится без остатка на 65.

Глава 3. АРИФМЕТИЧЕСКИЕ ПРИЛОЖЕНИЯ

ТЕОРИИ ЧИСЛОВЫХ СРАВНЕНИЙ

§ 8. СИСТЕМАТИЧЕСКИЕ ЧИСЛА

ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

1. ЦЕЛЫЕ СИСТЕМАТИЧЕСКИЕ ЧИСЛА

8. 1. Определение 1.

Системой счисления называется всякий способ записи чисел. Знаки, с помощью которых записывают эти числа, называют цифрами.

8. 2. Определение 2.

Целым неотрицательным систематическим числом, записанным в t -ичной позиционной системе счисления, называется число n вида

, где a_i (i = 0,1, 2,…, k) – целые неотрицательные числа – цифры, причём 0 £ a_i £ t – 1, t – основание системы счисления, tÎN, t > 1.

Например, запись числа в 7-ричной системе имеет вид: (5603)₇ = 5 ×7³ + 6×7² + 0×7¹ + 3. Здесь a_i – это 5, 6, 0, 3 – цифры; все они удовлетворяют условию: 0 £ a_i £ 6. При t =10 говорят: число n записано в десятичной системе счисления, причём индекс t=10не пишут.

8. 3. Теорема 1.

Всякое целое неотрицательное число может быть представлено, причём единственным образом, в виде систематического числа по любому основанию t, где t Î N, t > 1.

Пример: (1 3 9) ₁₀ = (3 5 1) ₆ = (1 0 2 4) ₅ = …

8. 4. Отметим, что:

1) приписывание к систематическому числу нулей слева не изменяет этого числа:

(3 4)₅ = (0 3 4)₅.

2) приписывание к систематическому числу s нулей справа равносильно умножению этого числа на t ^s: (3 4)₅ = 3×5¹ + 4; (3 4 0 0)₅ = 3×5³ + 4×5² + 0×5¹ + 0 = 5²×(3×5¹ + 4).

8. 5. Алгоритм перевода числа, записанного в t -ичной системе, в десятичную:

Пример: (287)₁₂ = 2×12² + 8×12¹ +7×12⁰ = 2×144 + 8×12 + 7 = 288 + 96 +7 = (391)₁₀.

8. 6. Алгоритм перевода числа, записанного в десятичной системе, в t -ичную:

Пример: (3 9 1)₁₀ = (х) ₁₂. Найти х.

Находим остатки от деления на основание системы t = 12: 1) данного числа 391 на 12, получим r1 = 7 ; 2) первого частного 32 на 12, получим r2 = 8 ; 3) второго частного 2 на 12, получим r3 = 2 ; Искомое число х составляется из остатков, записываемых последовательно, начиная с последнего: х = (2 8 7)12 .	391 36 31 24
32 24
2
8 = r2 0 0
7 = r1	2 = r3

8. 7. Действия над систематическими числами

осуществляются с помощью таблиц сложения и умножения размером t ´ t. Например, при t = 2 таблицы имеют вид:	+	0 1		´	0 1
	0 1 1 10		0 0 0 1

2. СИСТЕМАТИЧЕСКИЕ ДРОБИ

8. 8. Определение 3.

Конечной t-ичной систематической дробью в системе счисления с основанием t называется число вида

где c₀ÎZ , с_i – цифры – целые неотрицательные числа, причём 0 £ с_i £ t – 1, t Î N, t > 1, k Î N .

Обозначение: a = (c₀ , с₁с₂…с_k )_t. При t = 10 дробь называется десятичной.

8. 9. Следствие 1.

Всякая конечная систематическая дробь есть рациональное число, которое можно представить в виде 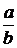, где а Î Z, b Î N.

Пример. a = (3 1, 2 4)₆ = 3×6 + 1 + =19 + – рациональное число. Обратное утверждение, вообще говоря, неверно. Например, дробь нельзя преобразовать в конечную систематическую (десятичную) дробь.

8.10. Определение 4.

Бесконечной t-ичной положительной систематической дробью в системе счисления с основанием t называется число вида

, где с₀ Î N, с_i (i =1, 2, …, к , …) – цифры – целые неотрицательные числа, причём 0 £ с_i £ t –1, tÎN, t >1, kÎN.

Обозначение: a = (с₀ , с₁ с₂ … с_k …) _t. При t =10 дробь называется десятичной.

8.11. Определение 5.

Возможны три вида бесконечных систематических дробей:

I a = (с₀ , )_t = = _t , где = = = … В этом случае число a называется бесконечной чисто периодической дробью, (с₁ с₂ … с_k) – периодом, k– количество цифр в периоде – длиной периода.

II a = .

В этом случае число a называется бесконечной смешанной периодической дробью, – предпериодом, ( ) – периодом, k – количество цифр в периоде – длиной периода, l – количество цифр между целой частью и первым периодом – длиной предпериода.

III a = (с₀, с₁ с₂ … с_k … )_t . В этом случае число a называется бесконечной непериодической дробью.

ТИПОВЫЕ ЗАДАЧИ

1. Число (а)₅ = (2 1 4 3) ₅, заданное в 5–ричной системе, перевести в 7-ричную систему, то есть найти х, если (2 1 4 3) ₅ = (х)₇ .

Решение.

1) Преобразуем данное число (2 1 4 3) ₅ в число (у)₁₀, записанное в десятичной системе:

(2 1 4 3) 5 = 2×53 +1×52 + 4×5 +3 = = 2×125 +1×25 + 4×5 +3 =250 +25 + 20+3 = (2 9 8) 10. 2) Преобразуем полученное число (у)10 в семеричную систему (х)7 (см. справа): Ответ: (2 1 4 3) 5 = (6 0 4) 7.	298 28 18 14 4 = r1
42 42
6
0 = r2	0 0 6 = r3

2. Выполните действия:

1) (7) ₈ + (5) ₈; 2) (7) ₈ × (5) ₈; 3) (3 6 4 2) ₆ + (4 3 5 1) ₆;

4) (5 2 3 4) ₇ – (2 3 5 1) ₇; 5) (4 2 3 ) ₅ × (3 2) ₅; 6) (3 0 1 4 1) ₅ : (4 2 3) ₅.

Решение.

1) (7) ₈ + (5) ₈ = (7) ₁₀ + (5) ₁₀ = (12) ₁₀ = 1×8 + 4 = (1 4) ₈ ;

2) (7) ₈ × (5) ₈ = (7) ₁₀ × (5) ₁₀ = (35) ₁₀ = 4×8 + 3 = (4 3) ₈ ;

3) (3 6 4 2)6 + (4 3 5 1)6 (1 2 4 3 3)6	Примечание:	4+5 = 9 = 1×6+3, 3 пишем, 1 переходит в следующий разряд, 6+3+1=10 =1×6+4, 4 пишем, 1 переходит в следующий разряд, 3+4+1= 8 = 1×6+2, 2 пишем, 1 переходит в следующий разряд.
4) (5 2 3 4)7 – (2 3 5 1)7 (2 5 5 3)7	Примечание:	"занимаем" единицу высшего разряда, т. е. "1" = 1×7: (3 + 1×7 ) – 5 = 10 – 5 = 5, (1 + 1×7 ) – 3 = 8 – 3 = 5,
5) (4 2 3)5 ´ ( 3 2)5 (1 4 0 1)5 +(2 3 2 4)5__ (3 0 1 4 1)5	Примечание:	При умножении на 2 : 3 ×2 = 6 = 1×5 + 1, 1 пишем, 1 переходит в следующий разряд, 2 ×2 +1=5 = 1×5 +0, 0 пишем, 1 переходит в следующий разряд, 2 ×4 +1=9 = 1×5 +4, 4 пишем, 1 переходит в следующий разряд, При умножении на 3 : 3 ×3 = 9 = 1×5 + 4, 4 пишем, 1 переходит в следующий разряд, 3 ×2 +1=7 = 1×5 +2, 2 пишем, 1 переходит в следующий разряд, 3 ×4 +1=13=2×5 +3, 3 пишем, 2 переходит в следующий разряд.

6) (3 0 1 4 1)₅ | (4 2 3)₅

2 3 2 4 (3 2)₅

1 4 0 1

1 4 0 1 Ответ: 1) (1 4)₈; 2) (4 3)₈; 3) (1 2 4 3 3)₆; 4) (2 5 5 3)₇;

(0)₅ 5) (3 0 1 4 1)₅; 6) (3 2)₅ .

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

151. Числа, заданные в t-ичной системе, переведите в десятичную систему:

а) (2 3 5) ₇ ; б) (2 4 3 1) ₅ ; в) (1 0 0 1 0 1) ₂ ; г) (1 3 )₁₅;

д) (2 7) ₁₁ ; е) (3 2 5 4) ₆ ; ж) (1 5 0 1 3) ₈ ; з) (1 1 0 1 1 0 0 1) ₂;

и) (7 6 2)₈; к) (1 1 1 1)₂₀.

152. Числа. заданные в десятичной системе, переведите в t-ичную систему. Сделайте проверку.

а) (1 3 2) ₁₀ = (х) ₇; б) (2 9 8) ₁₀ = (х) ₅ ; в) (3 7) ₁₀ = (х) ₂ ; г) (3 2 4 5)₁₀ = (х)₆;

д) (4 4 4 4) ₁₀ = (х) ₃; е) (5 6 3) ₁₀ = (х) ₁₂; ж) (5 0 0) ₁₀ = (х) ₈; з) (6 0 0) ₁₀ = (х) ₂;

и)(1 0 0 1 5)₁₀ =(х)₂₀; к) (9 2 5) ₁₀ = (х) ₈; л) (6 3 3) ₁₀ = (х) ₁₅; м) (1 4 3) ₁₀ = (х) ₂.

153. Числа, заданные в t-ичной системе, переведите в q-ичную систему (путём перехода через десятичную систему).

а) (3 7) ₈ = (х) ₃; б) (1 1 0 1 1 0) ₂ = (х) ₅; в) ( 6 2) ₁₁ = (х) ₄ ;

г) (4 )₁₂ = (х) ₉ . д) (3 3 1 3 1) ₅ = (х) ₁₂ .

154. а) Как изменится число (1 2 3) ₅ , если к нему справа приписать нуль ?

б) Как изменится число (5 7 6) ₈ , если к нему справа приписать два нуля ?

155. Выполните действия:

а) (3 0 2 1) ₄ + (1 2 3 3) ₄; б) (2 6 5 4) ₈ + (7 5 4 3) ₈; в) (1 0 1 1 0 1)₂+(1 1 0 1 10)₂;

г) (5 2 4 7) ₉ + (1 3 7 6) ₉; д) (4 7 6) ₉ – (2 8 7) ₉; е) (2 4 5 3) ₇ – (1 6 4 5) ₇;

ж) (8 3) ₁₂ – (5 7 9) ₁₂; з) (1 7 5) ₁₁ – ( 6) ₁₁; и) (3 6 4 0 1) ₇ – (2 6 6 6 3) ₇;

к) (1 0 0 1 0) ₂ × (1 1 0 1) ₂; л) (7 4 1) ₈ × (2 6) ₈; м) (5 3 7 2) ₈ × (2 4 6) ₈;

н) (3 3 2 1) ₄ × (2 3 0) ₄; о) (1 0 2 2 2 2) ₃ : (1 2 2) ₃; п) (2 1 0 3 2) ₄ : (3 2 3) ₄;

р) (2 6 1 7 4) ₈ : (5 4 6) ₈; с) (4 3 2 0 1) ₅ : (2 1 4) ₅; т)(1 1 0 1 0 0 1 0)₂:(1 0 1 0 1)₂

у) (1 1 0 1 1 0) ₂ : (1 1 1) ₂; ф) (1 1 1 0) ₆ : (2 1 5) ₆; х)(3 2 3 8 2 2 1 7 0)₉:(7 6 4 2)₉.

ц) (1 6 3 5) ₈ + (7 6 4 ) ₈; ч) (1 1 1 1) ₃ – (2 1 2) ₃; ш)(1 2 7)₁₂+(9 1 3 5 )₁₂

щ) (1 6 3 5) ₈ × (7 6 4) ₈; э) (9 5 7 2) ₁₁ × (3 2) ₁₁; ю)(2 1 2 7 4 5)₁₁ : (3 1)₁₁

я) (1 0 0 0 1 0 1 1 0 0 1) ₂ × (1 1 1 0 0 0 1) ₂ .

§ 9. ПЕРЕХОД ОТ РАЦИОНАЛЬНОГО ЧИСЛА ВИДА

К СИСТЕМАТИЧЕСКОЙДРОБИ

ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

9. 1. Установим условия, при которых число вида 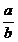, где а, b Î N, (а, b) =1, а < b, преобразуетсяв тот или иной вид систематической дроби (для случая, когда t = 10, то есть в десятичной системе счисления).

Пусть t = 10 = 2×5, а в числе знаменатель b имеет вид:

(q_i – простые числа), то есть b = b' × b₁ Тогда:

I Если знаменатель b = b' (содержит только "2" и / или "5"), – то дробь преобразуется в конечную десятичную дробь. Количество десятичных знаков равно наименьшему натуральному числу l, удовлетворяющему сравнению 10 ^l º 0(mod b' ).

II Если знаменатель b = b₁ (не содержит "2" и "5"), – то дробь преобразуется в бесконечную чисто периодическую десятичную дробь. Длина периода равна наименьшему натуральному числу k, удовлетворяющему сравнению 10 ^k º 1(mod b₁).

III Если знаменатель b = b' × b₁ (содержит "2" и / или"5", а также иные простые множители), – то дробь преобразуется в бесконечную смешанную периодическую деся-

тичную дробь.

Длина периода равна наименьшему натуральному числу k, удовлетворяющему сравнению 10 ^k º 1(mod b₁ ).

Длина предпериода равна наименьшему натуральному числу l, удовлетворяющему сравнению 10 ^l º 0(mod b' ).

9. 2. Выводы.

a	↗	к о н е ч н а я д е с я т и ч н а я д р о б ь		рацион. число   иррацион. число
↘	бесконечная десятичная дробь		1) чисто периодическая дробь 2) смешанная периодич. дробь 3) непериодическая дробь

9. 3. Отметим, что:

рациональным числом является всякая конечная десятичная дробь или бесконечная периодическая десятичная дробь;

иррациональным числом является всякая бесконечная непериодическая десятичная дробь.

ТИПОВЫЕ ЗАДАЧИ

1. Данные обыкновенные дроби, записанные в десятичной системе, преобразовать в

десятичные, предварительно определив вид искомой дроби (конечная или бесконечная; периодическая или непериодическая; если – периодическая, то чисто периодическая или смешанная периодическая); в последних случаях – предварительно найти число k – длину периода и число l – длину предпериода. 1) ; 2) ; 3) .

Решение.

1) У дроби = знаменатель – число b = 80 = 2⁴ × 5 содержит только "2" и "5". Поэтому данная дробь преобразуется в конечную десятичную дробь. Количество десятичных знаков l _наим определяется из условия: 10 ^l º0(mod80):

Имеем:10 1º10(mod80), 10 2= 100 º20(mod80), 10 3º200 º 40(mod80), 10 4º400 º 0(mod80).

Следовательно, l наим = 4, то есть искомая десятичная дробь будет иметь 4 десятичных знака. Проверка: разделим "уголком" 3 на 80 и получим: = 0, 0375.

2) У дроби = знаменатель – число b = 27 = 3³ не содержит "2" и "5". Поэтому данная дробь преобразуется в бесконечную чисто периодическую десятичную дробь. Длина периода k _наим определяется из условия: 10 ^k º1(mod27):

Имеем: 10 1º10(mod27), 10 2º100–81º19(mod27), 10 3º190 º190 – 7×27 º º 190 – 189 º 1(mod27).

Следовательно, k наим = 3, то есть в искомой десятичной дроби будет период длиной k = 3. Проверка: разделим "уголком" 2 на 27 и получим: = 0, (074).

3) У дроби = знаменатель – число b = 24 = 2³ ×3, то есть имеет вид: b = b' × b₁ (кроме "2" или "5" содержит и иные множители, в данном случае число 3). Поэтому данная дробь преобразуется в бесконечную смешанную периодическую десятичную дробь. Длина периода k _наим определяется из условия: 10 ^k º1(mod3), откуда k _наим = 1, то есть длина периода k = 1. Длина предпериода l _наим определяется из условия: 10 ^l º0(mod8), откуда l _наим = 3, то есть длина предпериода l = 3.

Проверка: разделим "уголком" 5 на 24 и получим: = 0, 208 (3).

Ответ: 1) 0, 0375; 2) 0, (074); 3) 0, 208 (3).

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

156. Данные обыкновенные дроби, записанные в десятичной системе, преобразуйте в десятичные дроби . Если десятичная дробь - периодическая, то предварительно найдите число k - длину периода и число l - длину предпериода.

157. Данные обыкновенные дроби, записанные в десятичной системе, преобразуйте в t-ичные систематические дроби. Найдите числа k - длину периода и l - длину предпериода.

158*. В какой системе счисления число (4 6) ₁₀ записывается теми же цифрами, но в

обратном порядке ?

159*. Что больше: единица 8-го разряда в двоичной системе или единица 4-го разряда в 8-ричной системе ?

§ 10. ТЕОРЕМА ПАСКАЛЯ. ПРИЗНАКИ ДЕЛИМОСТИ

ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

10. 1. Теорема Паскаля (1623 – 1662).

Даны натуральные числа: т > 1 и n, записанное в t - ичной системе:

, где a_i – – цифры: a_i ÎN, 0 £ a_i £ t –1 (i = 0,1, 2,…, k ), tÎN, t > 1.

Пусть

Итак: из равенства (*) в теореме Паскаля следует, что число n и число сравнимы по модулю т (а значит – равноостаточны при делении на т). Отсюда, в частности, вытекает, что если делится на т без остатка, то и n делится на т без остатка. Поэтому имеет место следствие:

10. 2. Следствие.

Для того, чтобы число n делилось без остатка на число т, необходимо и достаточно, чтобы сумма делилась без остатка на т:

(16)

ТИПОВЫЕ ЗАДАЧИ

1. Установите в десятичной системе счисления признаки делимости на 3, на 9 и на 11.

1) Признаки делимости на 3 и на 9.

Пусть n = (a_k a_{k – 1} … a₁ a₀)₁₀ = a_k ×10^k +a_{k – 1}×10^{k – 1}+…+a₁×10 + a₀, m =3 и m = 9.

1) Найдём b_i : по модулю m = 3по модулю m = 9

10⁰ º1(mod3), т.е. b₀ =1, 10⁰ º1(mod9), т.е. b₀ =1,

10¹ º1(mod3), т.е. b₁ =1, 10¹ º1(mod9), т.е. b₁ =1,

10² º1(mod3), т.е. b₂ =1, 10² º1(mod9), т.е. b