Расчет ведущего звена по методу Жуковского
В качестве проверочного расчета воспользуемся теоремой Жуковского. Для этого построим повернутый на 90° план скоростей приложим в соответствующие точки силы, действующие на звенья механизма . Кроме того, на звено 2 действует момент пары сил инерции. Его надо разложить на пары сил и приложить к концам звена с направлением, совпадающим с направлением момента
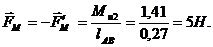
Эти силы прикладываем к соответствующим точкам повернутого плана скоростей.
Расставив все силы и определив плечи их действия относительно полюса плана, составим уравнение моментов этих сил относительно полюса:
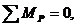
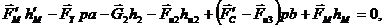
откуда
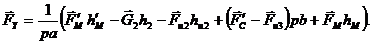
Подставляем числовые значения, получим:
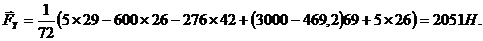
Погрешность при сравнении двух способов найдем из соотношения
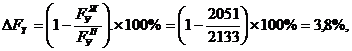
где 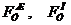 — уравновешивающие силы, определенные соответственно по методу Жуковского и по методу планов сил.
— уравновешивающие силы, определенные соответственно по методу Жуковского и по методу планов сил.
Ошибки при учебных инженерных расчетах допускаются 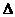 =±5 %. Следовательно, силовой расчет механизма выполнен в допускаемых пределах.
=±5 %. Следовательно, силовой расчет механизма выполнен в допускаемых пределах.
Синтез кулачкового механизма
Параметры кулачкового механизма:
а) наибольшая высота подъема толкателя h = 12 мм;
б) фазовый угол удаления 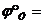 100°;
100°;
в) фазовый угол дальнего состояния 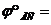 50°
50°
г) фазовый угол возвращения 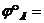 100°.
100°.
Проектирование механизма
Переведем фазовые углы в радианы:
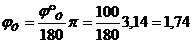 рад,
рад,
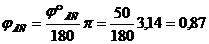 рад,
рад,
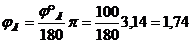 рад.
рад.
Рабочий угол кулачка составит:
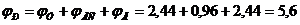 рад,
рад,
Примем по осям абсцисс кинематических диаграмм толкателя одинаковый масштаб 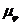 рад/мм. Тогда отрезки, отображающие фазовые углы на осях абсцисс, будут равны:
рад/мм. Тогда отрезки, отображающие фазовые углы на осях абсцисс, будут равны:
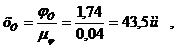
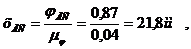

При параболическом движении толкателя (с постоянным ускорением) максимальное значение ускорения вычисляется по формуле
 ,
,
Скорость:
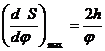 .
.
Используя эти формулы, вычислим максимальное значение ускорения и скорость толкателя при подъеме и опускания:
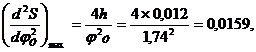
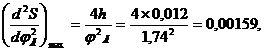
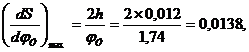
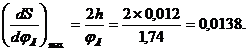
Приняв масштаб по осям ординат для всех диаграмм
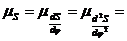 0.0002м/мм,
0.0002м/мм,
вычислим координаты
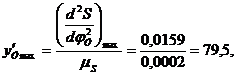
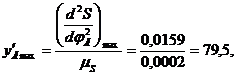
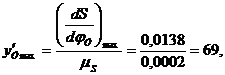
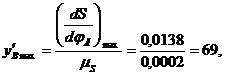
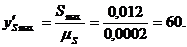
По вычисленным значениям построим диаграмму аналога ускорения. Для этого на оси абсцисс откладываем отрезки, отобрал фазовые углы, а по оси ординат — максимальные значения ускорения при подъеме и опускании.
С помощью графического интегрирования построим диаграмму аналога скоростей. Интегрирование диаграммы выполняется в порядке обратном графическому дифференцированию. На продолжении оси абсцисс влево от начала координат 02 откладываем полюсное расстояние Н2=Р2О2. Чтобы соблюсти принятый масштаб, вычислим величину полюсного расстояния по формуле
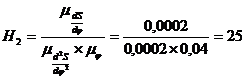 мм.
мм.
Проектируем на ось ординат точки 1", 2"и т. д. диаграммы аналога ускорений, проекции которых(точки а и b) соединяем с полюсом Р2.
Параллельно линии Р2b из начала координат О1 диаграммы аналогов скоростей проводим линию О14 до встречи с вертикалью, проведенной из точки 4 оси абсцисс. Из точки 4' проводим 4' — 8 параллельно Р2аи т. д.
Диаграмму перемещений можно построить двумя способами.
1. Метод графического интегрирования диаграммы аналога скоростей. Чтобы соблюсти принятый масштаб, величину полюсного расстояния вычислим по формуле
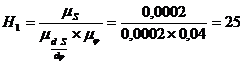 мм.
мм.
Из середины отрезков 01 -2, 2-4, 4-6 и т. восстанавливаем перпендикуляры до встречи с диаграммой аналога скоростей, а затем проводим горизонтальные линии до встречи с осью ординат. Полученные точки соединяем с полюсом Р1 . Параллельно линии Р1е из начала координат диаграммы перемещений 0 проводим линию 020 до встречи с вертикалью, восстановленной из точки абсцисс 2; из точки 20 проводим линию 2040, параллельную Р1f; източки 40 — линию 4060, параллельную Р1е, и т. д.
2. Аналитический метод. Диаграмма перемещения строится двух сопряженных ветвей парабол. Вершина одной параболы находится в начале координат, другой - в точке с координатами ( 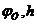 ). На оси ординат откладываем максимальный ход толкателя
). На оси ординат откладываем максимальный ход толкателя 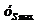 , а на оси абсцисс — фазовый угол удаления ху. Из середины отрезка ху восстановим перпендикуляр высотой
, а на оси абсцисс — фазовый угол удаления ху. Из середины отрезка ху восстановим перпендикуляр высотой 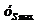 . Затем разделим его на то же число частей, что и отрезок, равный ху (на 8 частей). Из начала координат ху,
. Затем разделим его на то же число частей, что и отрезок, равный ху (на 8 частей). Из начала координат ху, 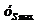 графика проводим лучи через точки 1у, 2у, 3у, 4у. Из точки с координатами ху,
графика проводим лучи через точки 1у, 2у, 3у, 4у. Из точки с координатами ху, 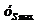 проводим лучи через точки 4у 5у 6у, 7у.Каждый луч, пересекаясь с одноименной ординатой дает точку, принадлежащую параболе.
проводим лучи через точки 4у 5у 6у, 7у.Каждый луч, пересекаясь с одноименной ординатой дает точку, принадлежащую параболе.
Аналогичным способом построим параболы и для фазы опускания толкателя. Для определения наименьшего радиуса профиля кулачка воспользуемся связью угла давления с размерами кулачка. Для этого путем графического исключения параметра 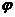 построим диаграмму функции
построим диаграмму функции
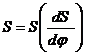
Проведем под углом 45° к оси абсцисс диаграмме аналогов скоростей наклонную линию ff. Из точек диаграммы аналогов скоростей проведем горизонтальные линии до встречи с наклонной, откуда проводим вертикальные линии до встречи с горизонтальными, проведенными из соответствующих точек диаграммы перемещений. Соединив полученные точки плавной кривой, получим диаграмму плеч. Проведем касательные к кривой под углом 30° к центру кулачка.
Точка пересечения касательных явится оптимальным геометрическим местом расположения центра вращения кулачка. Соединив последний с нулевым положением толкателя, получим величину минимального радиуса теоретического профиля кулачка Rmin.
Измерим минимальный радиус кулачка. Построим окружность минимального радиуса Rmin, разобьем эту окружность в соответствии с осью ординат. Из точек деления проведем дуги радиусами в центре окружности 0. На пересечении этих дуг с лучами, проходящими через точки деления окружности, принадлежащими профилю кулачка. Соединив все точки плавной кривой, построим теоретический профиль кулачка, уменьшив который на величину радиуса ролика 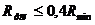 построим действительный профиль кулачка.
построим действительный профиль кулачка.
Синтез зубчатого механизма
Исходные данные:
т = 10 мм, z4 = 18, z5 = 25, i1H = 6.
