Алгоритм расчета методом сил

Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:

1. Определить степень статической неопределимости.

2. Выбрать основную систему.

3. Сформировать эквивалентную систему.

4. Записать систему канонических уравнений.

5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.

6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.

7. Построить суммарную единичную эпюру.

8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.

9. Решить систему канонических уравнений, т.е. определить реакции лишних связей.

10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).

11. Выполнить статическую и кинематическую проверки.

Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной.

Остановимся подробнее на некоторых из вышеперечисленных этапов расчета.

Выбор основной системы

Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной систе­мы. После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо ввести вместо связей неизвестные силовые факторы, которые принято называть лишними неизвестными. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы будем обозначать X_i, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы X_i, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.

Основную систему с приложенными к ней лишними неизвестными Х₁, Х₂ ,...X_n и внешней нагрузкой Р называют эквивалентной системой при условии, что её действительные перемещения согласуются с наложенными на исходную систему связями. Для каждой статически неопределимой заданной системы (рис. 10, а) можно подобрать, как правило, различные основные системы (рис. 10, б, в), однако их должно объединять следующее условие - основная система должна быть статически определимой и геометрически неизменяемой (т.е. не должна менять свою гео­метрию без деформаций элементов).

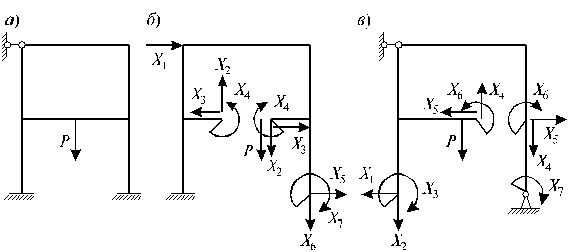
Рис. 10

Выбор основной системы (ОС) является непростым. Неудачный выбор ОС может привести к значительной трудоемкости решения, а иногда и к грубой ошибке. Нельзя руководствоваться только одним правилом образования основной системы, а именно, что число отбрасываемых связей должно быть равным степени статической неопределимости. Надо обязательно следить еще и за тем, какие связи отбрасываются. Некоторые связи отбрасывать недопустимо. При выборе основной системы надо следить кроме всего прочего и за геометрической неизменяемостью всей системы и отдельных ее частей.

Например, для рамы, показанной на рис. 11, можно предложить основные системы, а), б),..., которые получены путем отбрасывания семи дополнительных связей в различных комбинациях. Вместе с тем нужно помнить, что не всякая система с семью отброшенными связями может быть принята как основная. На рис. 12 показано три примера для той же рамы, в которой также отброшено семь связей, однако сделано это неправильно, так как оставшиеся связи не обеспечивают кинематической неизменяемости системы (рис.12, а, б), с одной стороны, и статической определимости во всех узлах,— с другой (рис.12, в).

Рис.11

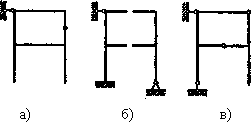
Рис.12

Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.

1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.13, б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.13, а).

2. Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n = 3 (рис.14, а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.14, б).

3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.14, в). В частных случаях (рис.14, г) рассечение стержня по шарниру освобождает две связи (рис.14, д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.14, е).

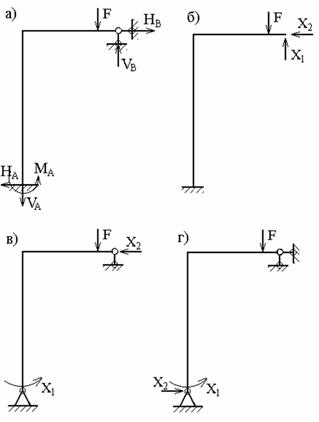
Рис. 13

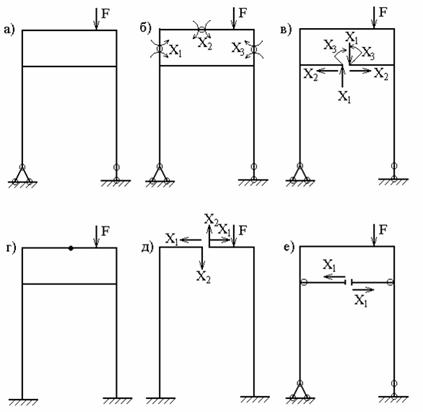
Рис. 14

Среди связей статически неопределимой системы различают абсолютно необходимые и условно необходимые. К абсолютно необходимым относятся связи, при удалении которых система становится геометрически изменяемой. Для абсолютно необходимой связи характерна статическая определимость усилия в ней, т.е. реакция такой связи может быть вычислена из условия равновесия. При выборе основной системы абсолютно необходимые связи отбрасывать нельзя.

Связи, при удалении которых система продолжает оставаться геометрически неизменяемой, называются условно необходимыми. Система, у которой удалили такую связь, может являться основной системой метода сил.

Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этой лекции. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.