Векторное произведение коллинеарных векторов

Определение подробно разобрано, осталось выяснить, что происходит, когда векторы 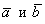коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы 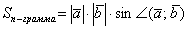– синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая

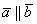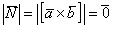Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.

Частный случай – векторное произведение вектора на самого себя:

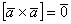
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.

Пример 1

а) Найти длину векторного произведения векторов 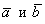, если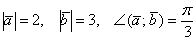

б) Найти площадь параллелограмма, построенного на векторах 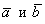, если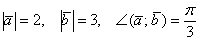

Решение: Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!

а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:

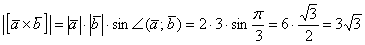
Ответ: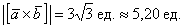

Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.

б) По условию требуется найти площадь параллелограмма, построенного на векторах 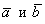. Площадь данного параллелограмма численно равна длине векторного произведения:

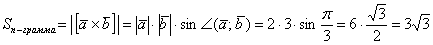
Ответ: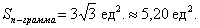

Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры, соответственно, размерность – квадратные единицы.

Популярный пример для самостоятельного решения:

Пример 2

Найти площадь треугольника, построенного на векторах 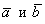, если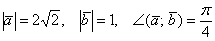

Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце.

Некоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.

Для произвольных векторов 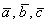и произвольного числа 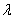справедливы следующие свойства:

1) 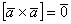В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.

2) 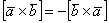– свойство тоже разобрано выше, иногда его называютантикоммутативностью. Иными словами, порядок векторов имеет значение.

3) 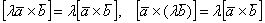– сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?

4) 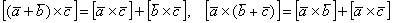– распределительные илидистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.

В качестве демонстрации рассмотрим коротенький пример:

Пример 3

Найти 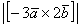, если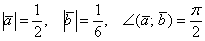

Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:

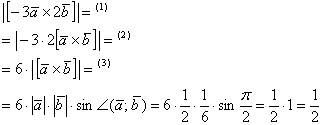
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.

(3) Дальнейшее понятно.

Ответ: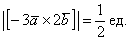

Пора подбросить дров в огонь:

Пример 4

Вычислить площадь треугольника, построенного на векторах 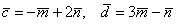, если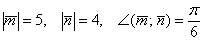

Решение: Площадь треугольника найдём по формуле 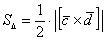. Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Решение для ясности разобьём на три этапа:

1) На первом шаге выразим векторное произведение 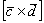через векторное произведение 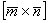, по сути, выразим вектор через вектор. О длинах пока ни слова!

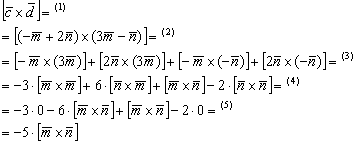
(1) Поставляем выражения векторов .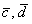

(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.

(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.

(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству 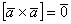. Во втором слагаемом используем свойство антикоммутативности векторного произведения: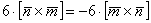

(5) Приводим подобные слагаемые.

В результате вектор оказался выражен через вектор, чего и требовалось достичь:

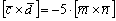
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:

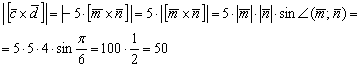
3) Найдём площадь искомого треугольника:

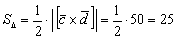
Этапы 2-3 решения можно было оформить и одной строкой.

Ответ: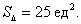

Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:

Пример 5

Найти 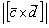, если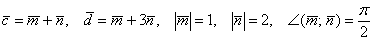

Краткое решение и ответ в конце.

Векторное произведение векторов в координатах

С векторами, заданными в координатах, всё тоже просто и прозрачно. Сразу обращаю внимание на то, что разговор пойдёт о координатах ортонормированного базиса. В общем случае аффинного базиса нижеприведённая формула будет нерабочей.

Векторное произведение векторов 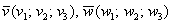, заданных в ортонормированном базисе 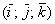, выражается формулой:

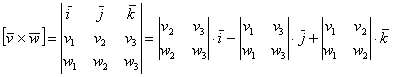
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов 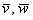, причём укладываем в строгом порядке – сначала координаты вектора «в», затем координаты вектора «дубль-в». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:

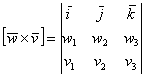
Согласно свойствам определителя, если в определителе две строки переставить местами, то он сменит знак. Этот факт полностью соответствует свойству антикоммутативности векторного произведения.

Данный определитель всегда раскрываем по первой строке, что продемонстрировано выше.

Что получается в результате раскрытия определителя?

В результате получается ВЕКТОР. А как иначе? Векторное произведение – это же вектор.

Пример 6

Найти векторное произведение векторов 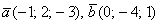и его длину.

Решение: Задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), а во-вторых – его длину.

1) Найдём векторное произведение:

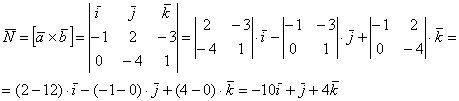
В результате получен вектор 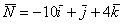, или, ещё можно записать .

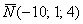Существует очень хороший способ проверки: как следует из определения, вектор 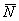должен быть ортогонален векторам 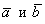. Ортогональность векторов, как мы разбирались, проверяется с помощью скалярного произведения:

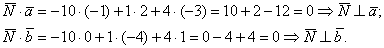
Если получилось хотя бы одно число, отличное от нуля, ищите ошибку в раскрытии определителя.

2) Вычислим длину векторного произведения.

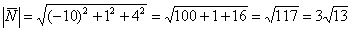
Ответ: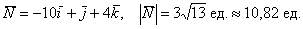

В плане технических обозначений здесь, наоборот, вместо громоздкой конструкции 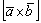выгодно использовать букву 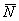, поскольку она сокращает запись

Аналогичный пример для самостоятельного решения:

Пример 7

Даны векторы 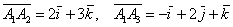. Найти 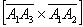и вычислить .

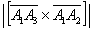Решение с ответом в конце!

Пример 8

Даны вершины треугольника 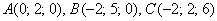. Найти его площадь.

Решение: Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы:

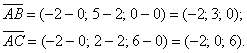
Затем векторное произведение:

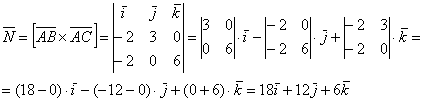
Вычислим его длину:

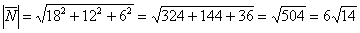
Формулы площадей параллелограмма и треугольника, само собой, остаются те же самые:

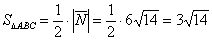
Ответ: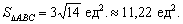

Рассмотренную задачу можно решить ещё двумя способами – было не обязательно выбирать стороны 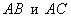. Решение также допустимо провести через векторы 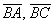либо 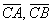. Желающие могут проверить, что во всех трёх случаях получится один и тот же ответ. Настоятельно рекомендую выполнить схематический рисунок, чтобы лучше понять вышесказанное.

Еще одна важная особенность состоит в том, что в задачах на нахождение площади фигуры порядок векторов не имеет значения. Действительно, если находить 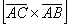, то получим противоположно направленный вектор 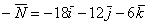, но формула вычисления длины вектора всё равно «съест» эти минусы. Заметьте, что такую перестановку нельзя делать в Примерах №№6,7, поскольку там требовалось найти вполне конкретный вектор.

Пример 9

Вычислить площадь параллелограмма, построенного на векторах 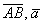, если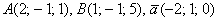

Это пример для самостоятельного решения.

В заключение первого раздела рассмотрим обещанную задачу Пример 10

Проверить, будут ли коллинеарны следующие векторы пространства:
а)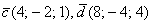
б)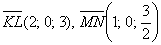

Решение: Проверка основана на одном из утверждений данного урока: если векторы 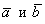коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .

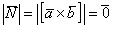а) Найдём векторное произведение:

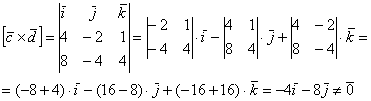
Таким образом, векторы 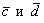не коллинеарны.

б) Найдём векторное произведение:

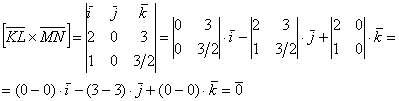
Значит,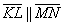

Ответ: а) не коллинеарны, б)