Линейные интегральные уравнения.

Интегральными уравнениями называют уравнения, в которых неизвестная функция входит под знак интеграла.

Основные классы линейных интегральных уравнений:

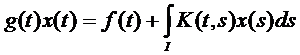(1)

(1) – общий вид, неизвестная функция входит линейно.

1) 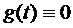, 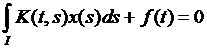– интегральное уравнение первого рода.

2) 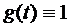, 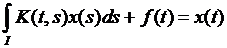– интегральное уравнение второго рода.

3) 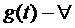функция, интегральное уравнение (1) третьего рода.

Функция 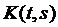, называется ядром интегрального уравнения.

Если 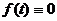, то интегральное уравнение называется однородным.

Ядро 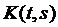и функция 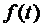– непрерывны, первая на , вторая на .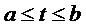

Уравнение 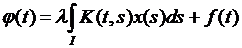(2) называется уравнением Фредгольма 2-ого рода, причём это семейство уравнений, зависящих от числового параметра .

Уравнением Фредгольма 1-ого рода имеет вид: 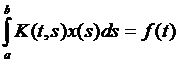(3)

Линейным интегральным уравнением Вольтера 2-ого рода называется уравнение: 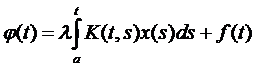, 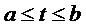(4)

неизвестная функция.

Уравнением Вольтера 1-ого рода называется уравнение: 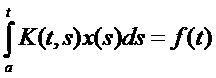(5)

Уравнение Вольтера можно рассматривать частный случай уравнение Фредгольма.

Ядро 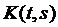определено при .

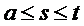Доопределяем по при 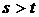следующим образом , .

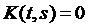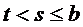Тогда уравнение (4) можно рассматривать, как частный случай уравнения Фредгольма с ядром 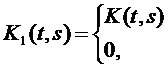, для

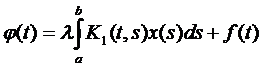(6)

Интегральные уравнения в общем виде в квадратурах не решается.

Задачи, приводящиеся к интегральным.

Одной из первых задач, связанной с интегральными уравнениями, была задача обращения интеграла.

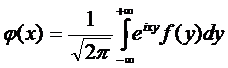(1).

Решение этой задачи получил Фурье:

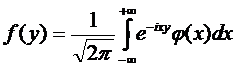(2)

К интегральным уравнениям типа Вольтера приводит задача Коши для обыкновенного дифференциального уравнения.

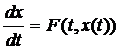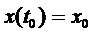, (3)

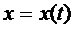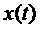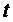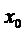Если есть решение дифференциального уравнения (3), то подставляя в уравнение (3) и интегрируя по от до 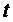, получим:

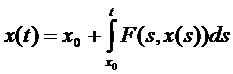(4).

Уравнения (3) и (4) – эквивалентны.

Рассмотрим уравнение: 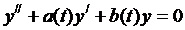с условиями 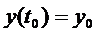, 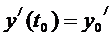(5)

Свести задачу Коши для данного уравнения к интегральному уравнению.

Обозначим 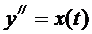, тогда .

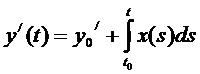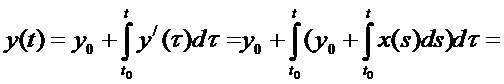
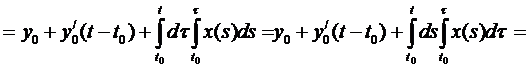
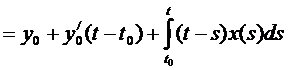
Итак, ,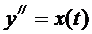

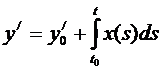
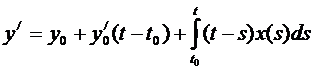(6)

Подставляя в исходное уравнение, получим:

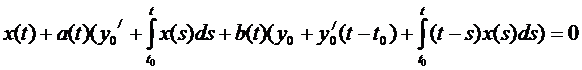(7)

или

,

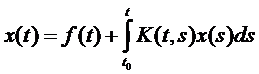где ,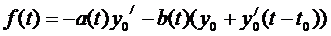

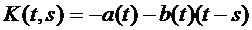(8).

Получим уравнение Вольтера или 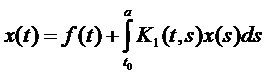– уравнение Фредгольма.

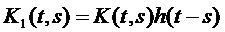, где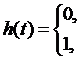

ЛЕКЦИЯ 13.

Теорема о существовании и единственности решения линейного интегрального уравнения Фредгольма 2-го рода с параметром.

Рассмотрим уравнение 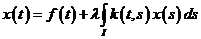(1)

– постоянное число, может быть комплексным.

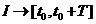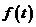; и 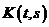- непрерывные функции и, следовательно, ограничены, т.е. . (2) ,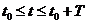

Будем доказывать существование и единственность решения уравнения (1), используя принцип сжатых изображений.

Принцип сжатых изображений.

Теорема. Если в полном метрическом пространстве М задан оператор А, удовлетворяющий следующим условиям:

1) Оператор А переводит точки пространства М в точки того же пространства, т.е. , то ;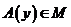

2) Оператор сближает точки, т.е.

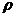; - расстояние между точками, не зависит от выбора точек 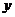и z.

Тогда существует единственная неподвижная точка , что , и эта точка может быть найдена методом последовательных приближений, т.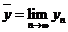е. , где 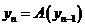(3), причем .

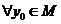Пояснения к теореме.

Ι. Пространство М называется метрическим, если в нём определена функция , удовлетворяющая следующим условиям:

1. ;

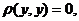
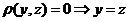2. ;

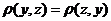3. .

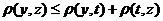Здесь, 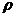называется расстоянием.

ΙΙ. Метрическое пространство называется постоянным, если любая фундаментальная последовательность точек пространства М сходится в этом пространстве. Последовательность 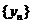называется фундаментальной, если для 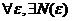, что 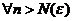для и для : .

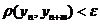Доказательство.

Покажем, что 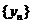(3) - фундаментальная последовательность.

(4)

Итак, 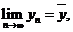(в силу полноты пространства М). Покажем, что 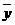неподвижна.

Пусть .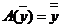

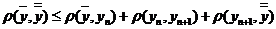
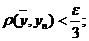
так как последовательность фундаментальная.

.

Итак, . Следовательно, .

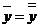
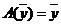Докажем, что эта точка единственная. Предположим, что есть ещё одна z такая, что A(z) = z.

Тогда , что противоречит второму условию теоремы.

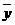- единственная точка.

Применим принцип сжатых отображений для доказательства теоремы о существовании и единственности решения уравнения (1).

Рассмотрим функциональное пространство непрерывных функций, заданных на промежутке I. Под расстоянием на этом пространстве между двумя любыми элементами этого пространства будем понимать (5).

Пространство является полным. Т.е. фундаментальная последовательность имеет предел, принадлежащий этому пространству:

.

В полном метрическом пространстве существует единственная неподвижная точка у оператора сжатых отображений. Ах = х.

Обозначим: - интегральный оператор.

Тогда (6) и уравнение (1) будет иметь вид х = Ах (7). Если мы докажем, что А – оператор сжатых отображений, то тем самым будет доказано, что уравнение (1) имеет единственное решение.

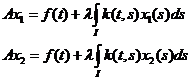(8)

.

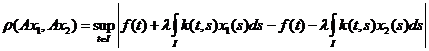(9).

Если сделать , то оператор будет сжимающим, т.е. (10). Параметр с таким условием называется малым.

Уравнение Фредгольма (1) с условием (10) имеет единственное решение. Если Т – переменная величина, т.е. уравнение (1) есть уравнение Вольтера, то можно сделать за счёт малости интервала по t. Уравнение Вольтера имеет единственное решение на достаточно малом промежутке.

Рассмотрим однородное уравнение Фредгольма 2-го рода: 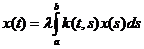(11).

Если 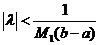, то существует только тривиальное, нулевое решение.

Те значения λ, при которых однородное уравнение (11) имеет решения, отличные от нулевого, называются собственными решениями.

Замечание.

Так как уравнение Вольтера имеет единственное решение при любом λ, то уравнение Вольтера не имеет собственных значений и собственных решений.