Простейшие типы точек покоя.

Рассмотрим линейную систему с постоянными коэффициентами

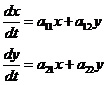(1) и исследуем расположение траекторий в окрестности точки покоя x = 0, y = 0.

Пусть 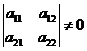(2) тогда 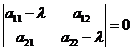(3).

Тем самым мы предполагаем, что корни характеристического уравнения (3) отличны

от нуля.

Ι. Характеристическое уравнение имеет действительные и различные корни.

1) 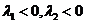. Общее решение имеет вид 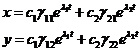(4).

Тогда точка х = 0, у = 0 асимптотически устойчива, так как все точки, находящиеся в момент t = t₀ в любой 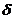-окрестности начала координат (при 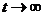) стремятся к началу координат.

Такая точка покоя называется устойчивым узлом.

2) 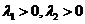. Точка покоя неустойчива, так как движущаяся по траектории 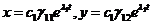точка с возрастанием t покидает 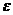-окрестность начала координат. Можно отметить, что есть движения, приближающиеся к началу координат: .

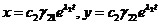ΙΙ. Корни характеристического уравнения (3) являются комплексными.

.

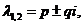
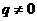Общее решение записывается в виде:

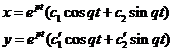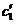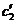(5), где и - линейные комбинаци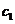и и .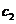

1) .

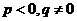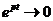с возрастанием t, а второй множитель является ограниченным. Точки, находящиеся при в любой 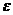- окрестности начала координат, попадают в 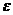-окрестность при возрастании t. Такая точка покоя называется устойчивым фокусом.

Фокус отличается от узла тем, что касательная к траекториям не стремится к определённому пределу при приближении точки касания к точке покоя.

2) .

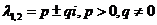Траектории те же, но движение по ним происходит в обратном направлении. Точка покоя неустойчива. Это неустойчивый фокус.

3) .

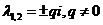В силу периодичности решений, траектории – замкнутые кривые, содержащие внутри себя точку покоя, которая в этом случае называется центром. Центр является устойчивой точкой покоя (но асимптотически устойчивой точкой его назвать нельзя).

ΙΙΙ. Корни кратные ( ).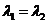

1) 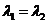< 0.

Общее решение имеет вид 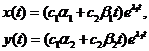(6), причём, здесь возможна ситуация, когда .

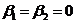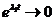при 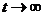. Точки покоя называются устойчивыми узлами. Если ,

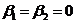то такой узел называется дикритическим (устойчивый).

2) 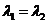>0.

Траектории не отличаются от траектории предыдущего случая, но движение по ним происходит в обратном направлении. В этом случае точка называется неустойчивым узлом.

Рассмотрим случай, когда .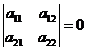

Тогда характеристическое уравнение (3) имеет нулевой корень 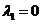. Предположим, что 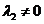. Тогда общее решение имеет вид:

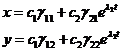(7).

Исключая из системы (7) t, получим семейство параллельных прямых:

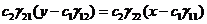(8).

Если с₂ = 0, получим однопараметрическое семейство точек покоя, расположенных на прямой 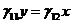. Если 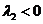, то при 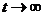на каждой траектории точки приближаются к лежащей на этой траектории точке покоя .

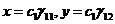Точка покоя х = 0, у = 0 устойчива, но асимптотической устойчивости нет.

Если же 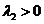, то траектории расположены также, но движение точек на траекториях покоя осуществляется в противоположном направлении. Точка покоя х = 0, у = 0 неустойчива.

3) .

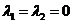В этом случае можно выделить два подпункта:

1. Общее решение имеет вид: 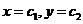- все точки являются точками покоя, все решения устойчивы.

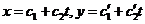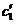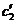2. Общее решение имеет вид: , и - линейные комбинаци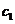и и 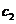. Точка покоя х = 0, у = 0 неустойчива.

ЗАМЕЧАНИЕ. Точки покоя х = 0, у = 0 системы (1) является особой точкой уравнения .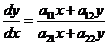

ЛЕКЦИЯ 12:

Результат об устойчивости и неустойчивости точки покоя , .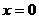

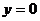Система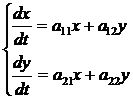

Можно распространить и на линейную систему с постоянными коэффициентами 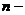го порядка:

,

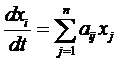Если все действительные части корней характеристического уравнения отрицательны, то тривиальное решение это 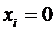, асимптотически устойчиво.

Если хоть один корень имеет действительную положительную часть, то неустойчиво.

Второй метод Лагранжа.

Рассматривается система 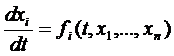(1)

Теорема 1:

Если существует дифференцируемая функция 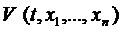, называемая функцией Ляпунова, удовлетворяющая в окрестности начала координат следующим условиям:

1) 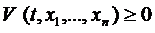, причём 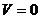лишь при , .

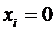2) 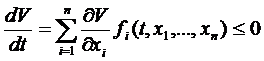, при 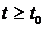, то точка покоя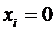 системы (1) устойчива.

Производная 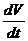в условии 2) взята вдоль интегральных кривых системы (1).

Доказательство:

Поверхности уровня в окрестности точки покоя, которая является точкой строгого минимума, являются замкнутыми и окружают точку покоя.

Рассмотрим поверхность уровня 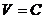, которая целиком лежит в 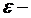окрестности, т.е. 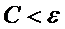, но не проходит через начало координат. Выберем 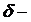окрестность так, чтобы 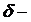окрестность целиком лежала внутри поверхности 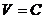. Если начальная точка с координатами 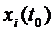, находилась в 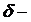окрестности, то 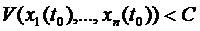, то при 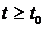точка траектории, которая проходит через точку 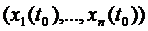не выйдет за пределы 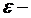окрестности начала координат в силу условия 2) теоремы.

Теорема 2: (т. Ляпунова для ассимптотичной устойчивости)

Если существует дифференцируемая функция Ляпунова 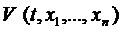, удовлетворяющая следующим условиям:

1) 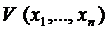имеет строгий минимум в начале координат .

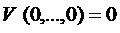2) производная функция 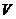, вычисляемая вдоль интегральных кривых системы (1):

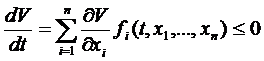, причём вне сколь угодно малой окрестности начала координат, т.е. при 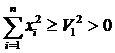, 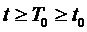производная 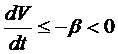, где 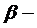постоянная, то точка покоя 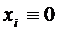, системы (1) асимптотически устойчива.

Доказательство:

Условия теоремы выполнены, то если 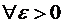можно выбрать 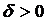, что траектория, начальная точка которой не выйдет из 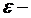окрестности начала координат.

Вдоль траектории функция 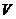монотонно убывает с возрастанием 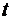. Следовательно, существует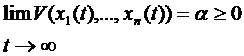

Надо показать, что 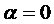. Откуда будет следовать, что , .

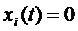Первое условие теоремы 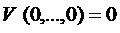только в начале координат.

Допустим, что .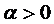

Тогда 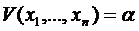возьмём за 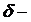окрестность, но здесь 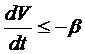, проинтегрируем это неравенство от 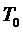до :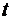

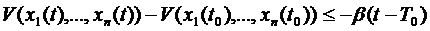
или

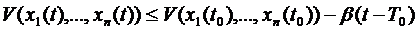
При достаточно большом 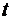правая часть отрицательна и , следовательно, 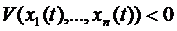, что противоречит условию 1).

Пример 1:

,

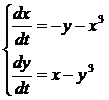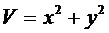
1) ,

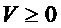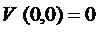
2)

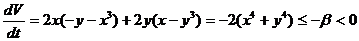
Решение 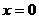, 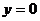асимптотически устойчиво.

Пример 2:

,

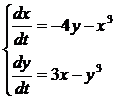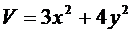
1) ,

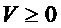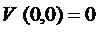
2)

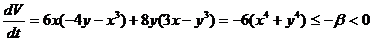
Решение 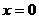, 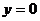асимптотически устойчиво.

Исследование проблемы устойчивости по первому приближению.

При исследовании на устойчивость точки покоя 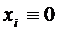, системы 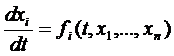(1), где 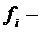дифференцируемая окрестности начала координат функция.

Применяется следующий метод:

Систему (1) представляют в окрестности начала координат:

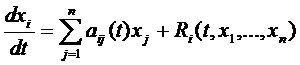, (2)

Система 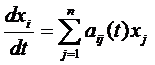, (3)

Называется системой первого приближения для системы (1).

Теорема 3:

Если система (2) стационарна в первом приближении, все числа 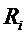, в достаточно малой окрестности начала координат при 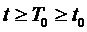удовлетворяют неравенствам:

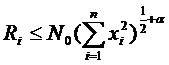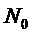, где и 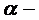постоянные.

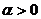и все корни характеристического уравнения:

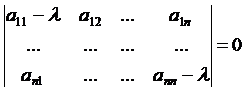(4)

имеют отрицательные действительные части, то тривиальное решение 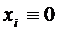, системы (1) асимптотически устойчиво.

Теорема 4:

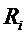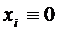Если система (2) стационарна в первом приближении, все функции , удовлетворяют условиям предыдущей теоремы, и хотя бы один корень характеристического уравнения (4) имеет положительную действительную часть, то точка покоя , системы (2) неустойчива.

В критическом случае, когда действительная часть и хотя бы одного корня равна нулю, на устойчивость начинают влиять нелинейные члены 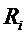и исследование на устойчивость по первому приближению невозможно.

Пример 1:

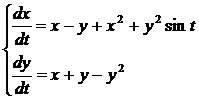
Нелинейные члены удовлетворяют условиям теорем 3. и 4. Исследуем на устойчивость точку покоя , .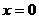

,

,

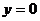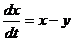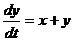
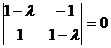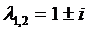
Решение 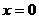, 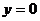неустойчиво.

Пример 2:

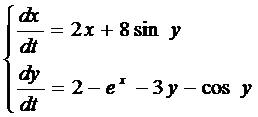
Разлагая по формулам Тейлора, получим:

, ,

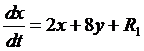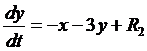где 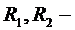удовлетворяют теоремам 4. и 5.

,

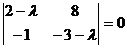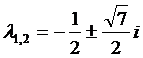
Решение 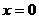, 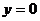асимптотически устойчиво.