Фундаментальная система решений.
Совокупность 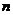 решений однородной системы (2), определенный и линейно независимыми в интервале
решений однородной системы (2), определенный и линейно независимыми в интервале 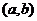 , называется фундаментальной системой решений в интервале
, называется фундаментальной системой решений в интервале 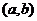 .
.
Кратко, 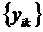 ,
,  ,
, 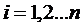 (19).
(19).
Теорема:
Система (2) всегда имеет ФСР в области непрерывности коэффициентов системы.
Возьмём 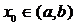 и построим
и построим 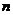 решений
решений
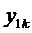 ,
, 
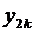 ,
, 
… (20)
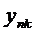 ,
, 
со следующими начальными условиями:
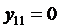 ,
, 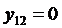 ,…,
,…, 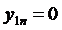 , при
, при 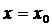
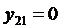 ,
, 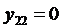 ,…,
,…, 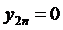 , при
, при 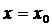
…… (21)
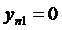 ,
, 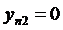 ,…,
,…, 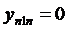 , при
, при 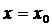
Вронскиан решений (20) в точке 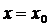 равен единице.
равен единице.
Следовательно, совокупность решений (20) линейно независима и является ФСР.
Из доказательства теоремы следует, что фундаментальных систем существует бесконечное множество. Построенная фундаментальная система (21) называется нормированной в точке 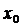 . Для каждой точки
. Для каждой точки 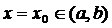 существует только одна нормированная в этой точке ФСР.
существует только одна нормированная в этой точке ФСР.
Построение общего решения.
Знание ФСР даёт возможность построения общего решения системы (2).
Основная теорема:
Если 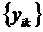 ,
,  ,
, 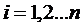 есть фундаментальная система решений в интервале
есть фундаментальная система решений в интервале 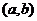 , то формулы
, то формулы 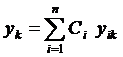 ,
,  (22), где
(22), где
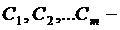 произвольные постоянные, дают общее решение системы в области
произвольные постоянные, дают общее решение системы в области  ,
, 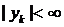 ,
,  .
.
Действительно, система (22) разрешима относительно 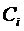 , так как
, так как 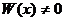 , кроме этого совокупность функций (22) является решением системы (2), что соответствует определению общего решения нормальной системы дифференциальных уравнений. Чтобы найти частное решение, удовлетворяющее условиям
, кроме этого совокупность функций (22) является решением системы (2), что соответствует определению общего решения нормальной системы дифференциальных уравнений. Чтобы найти частное решение, удовлетворяющее условиям  при
при 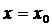 нужно подставить эти условия в систему (22).
нужно подставить эти условия в систему (22).
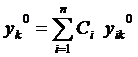 ,
,  (230
(230
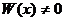 находим
находим  , откуда следует, что
, откуда следует, что 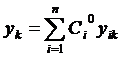 ,
,  (24) – есть искомое решение.
(24) – есть искомое решение.
Построение однородной линейной системы линейных уравнений, имеющей заданную ФСР.
Дано 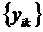 ,
,  ;
; 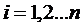 (25)
(25)
Подставляем поочерёдно решения (25) в 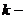 ое уравнение системы (2)
ое уравнение системы (2)
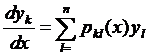 ,
,  ,
,
получим
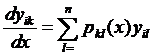 ,
, 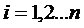 , (26)
, (26)
Отсюда определяются все 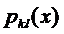 ,
, 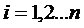 единственным образом.
единственным образом.
Эту систему можно записать:
 (27)
(27) 
Пример:
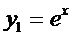 ,
, 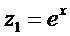
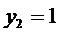 ,
, 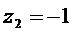
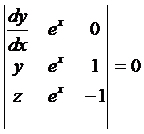 ,
, 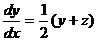 ,
,
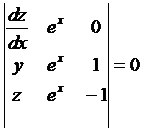 ,
, 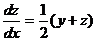
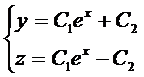
Общее решение неоднородной системы.
Теперь рассмотрим неоднородную систему (1): 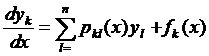 ,
,  . (1)
. (1)
Введём новые функции 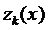 :
:
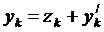 ,
,  (28), где
(28), где 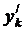 - решение неоднородной системы (1).
- решение неоднородной системы (1).
Подставляя (28) в систему (1), получаем: 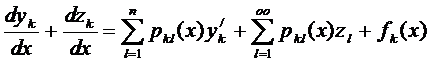 ,
,  (29)
(29)
Или, учитывая, что 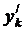 - решение неоднородной системы (1), получаем:
- решение неоднородной системы (1), получаем:
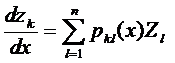 ,
,  (30)
(30)
(30) – есть однородная система, соответствующая системе (1), общее решение которой имеет вид: 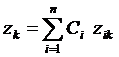 ,
,  (31)
(31)
Таким образом, подставляя (31) в (28) получаем:
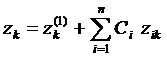 ,
,  (32)
(32)
Это формула есть общее решение системы (1) во всей области задания системы.
26. Метод вариации произвольных постоянных (метод Лагранжа)
Теорема:
Если известна ФСР однородной системы (2), то общее решение неоднородной системы (1) может быть найдено при помощи квадратур.
Будем искать решение неоднородной системы (1) в виде:
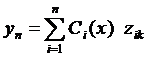 ,
,  (33)
(33)
где 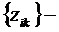 ФСР однородной системы (2), а
ФСР однородной системы (2), а 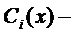 неизвестная непрерывно дифференцируемая функция.
неизвестная непрерывно дифференцируемая функция.
Подставим (33) в (1), получаем:
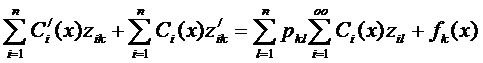
или
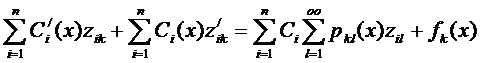
или
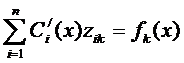 ,
,  (34)
(34)
Решая систему (34), определитель которой 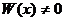 в интервале
в интервале 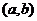 , получаем
, получаем
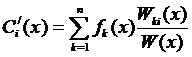 ,
,
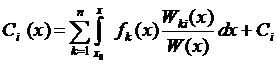 ,
, 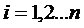 (35)
(35)
Подставляя (35) в выражение (33) получаем
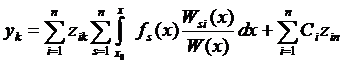 ,
,  (35)
(35)
Пример:
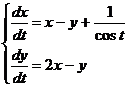
Решая соответствующую однородную систему, получаем:
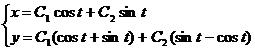
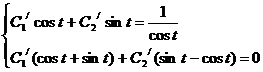
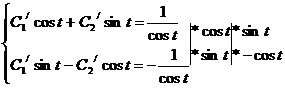
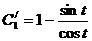
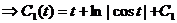
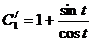
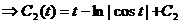
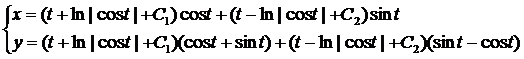
ЛЕКЦИЯ 9:
