Арифметика полиномов, заданных над конечным полем

Рассмотрим полином

,

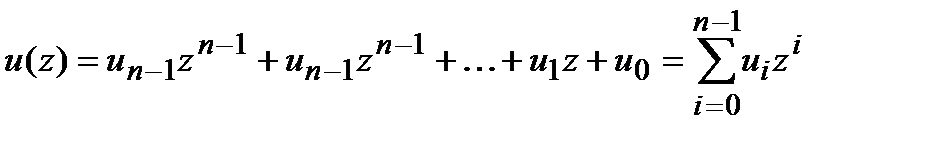в котором коэффициенты 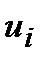являются элементами поля .

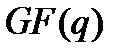Введем основные правила арифметических действий с формальными полиномами, коэффициенты которого принадлежат полю 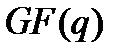(подобные полиномы обычно называют полиномами над ).

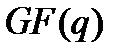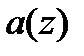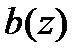1. Суммой двух полиномов и называется полином, определяемый соотношением:

.

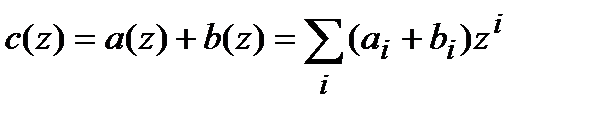2. Умножение полинома 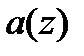на скаляр 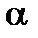(где 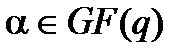) осуществляется как

.

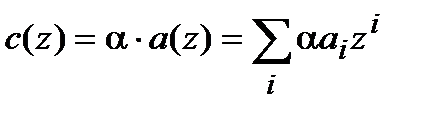Установив операции сложения полиномов и умножения полинома на скаляр, можно сказать, что множество полиномов 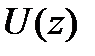кодовых слов обладает структурой векторного пространства и для него справедливы утверждения:

– если 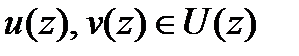, то ;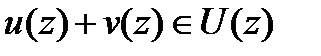

– если 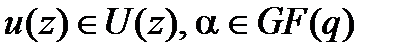, то .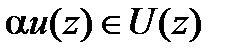

Рассмотрим некоторые определения, связанные с полиномами, заданными над конечным полем.

Пусть имеется многочлен .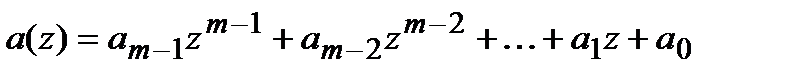

Приведенным (или нормированным) полиномом называется полином, старший коэффициент которого .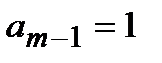

Нулевымполиномом называется полином .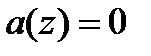

Степенью ненулевого полинома 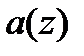называется наибольшая степень формальной переменной 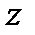при ненулевом коэффициенте 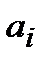и обозначается как .

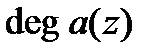Важную роль играет операция умножения полиномов, которая не определена для векторного пространства. Считая, что для формальных полиномов выполняется обычный дистрибутивный закон и что 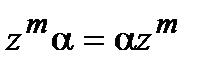, произведение полиномов задается соотношением, ничем не отличающимся от обычного произведения полиномов, изучаемого в школьной алгебре.

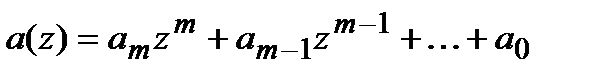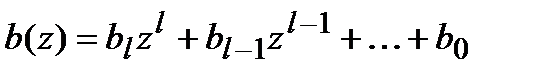Если и , то

,

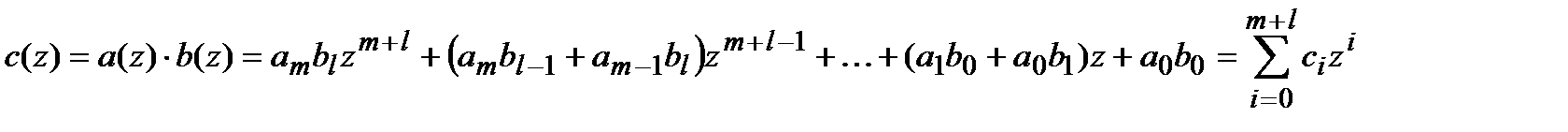где .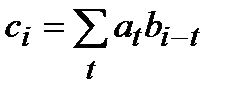

В современной алгебре структура, отличающаяся от поля только отсутствием обратимости ненулевых элементов, т.е. отсутствием операции деления, называется кольцом. Очевидно, что множество полиномов над полем 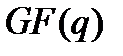образуют кольцо.

Другим, более известным примером кольца является множество целых чисел. Однако в кольце целых чисел операция умножения порождает еще одну, называемую делением с остатком. Возьмем некоторое положительное целое число 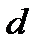. Тогда любое целое число 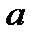может быть представлено в виде

,

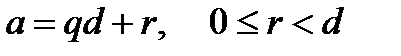где неотрицательное целое 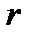, меньшее 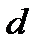, называется остатком (от деления 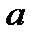на 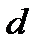), 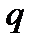называется частным от деления, 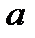– делимым, а 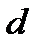– делителем.

Поскольку в кольце полиномов определена операция умножения, то, поступая аналогично, можно ввести операцию деления полиномов с остатком. Однако, для полиномов сравнение в терминах «больше–меньше» невозможно, поэтому для получения остатка сравниваются степени полиномов. Возьмем полином 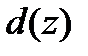и представим произвольный полином 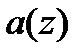как

.

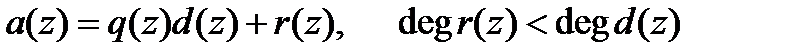В данном соотношении, возможном для любых 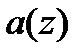и 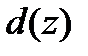, назовем полиномы 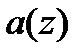, , 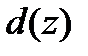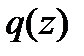и 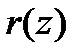делимым, делителем, частным и остатком соответственно. Операция деления полиномов известна под названием алгоритма Евклида. Определение частного и остатка от деления полиномов осуществляется «в столбик», как и при делении целых чисел.

В теории кодирования особая роль принадлежит остатку от деления, который часто называют вычетом многочлена 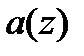по модулю многочлена 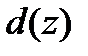. Данному определению соответствует запись

,

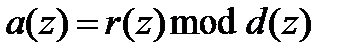которая символизирует, что полиномы 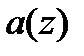и 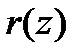имеют один и тот же остаток от деления на 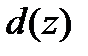. Действительно, 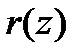является остатком от деления 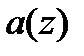на 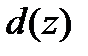. С другой стороны, поскольку 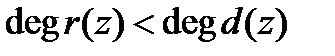, то 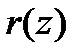сразу же является остатком от деления на .

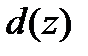Если 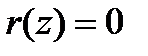, т.е. 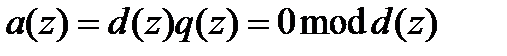, то говорят, что 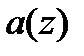делится на 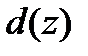, или 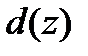делит 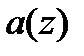, или 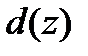является множителем 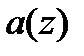. Используется также выражение, что 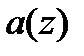раскладывается на множители меньшей степени.

Полином, который не может быть разложен на множители меньшей степени, называется неприводимым.

Наибольшим общим делителем двух полиномов 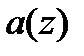и 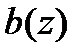, обозначаемым как 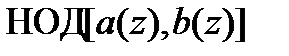, называется приведенный полином наибольшей степени, делящий одновременно оба из них.

Наименьшим общим кратным двух полиномов 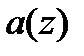и 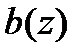, обозначаемым как 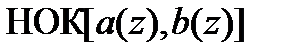, называется приведенный полином наименьшей степени, делящийся на оба из них.

Если наибольший общий делитель двух полиномов равен единицы, т.е. 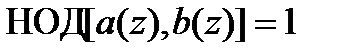, то они называются взаимно простыми.

Расширенные конечные поля

Теперь у нас есть все необходимые сведения, чтобы расширить поле 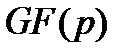до поля 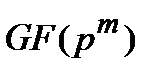( 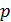– простое число).Как уже известно, существуют конечные поля только порядка 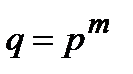( 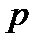– простое, 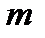– натуральное числа). Простое поле 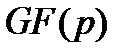порядка 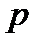может трактоваться как множество остатков от деления целых чисел на 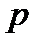: 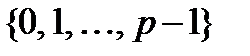с операциями сложения и умножения по модулю 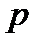. Аналогичным образом расширенное поле 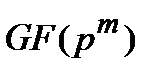порядка 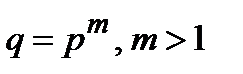, может трактоваться как множество остатков от деления полиномов над 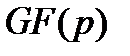на некоторый неприводимый полином 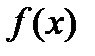степени 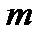с операциями сложения и умножения по модулю 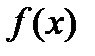. Другими словами, поле 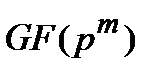содержит все полиномы над полем 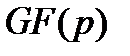степени не выше 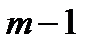с общепринятыми операциями сложения и умножением, осуществляемым в два этапа – вначале производится обычное умножение полиномов, а затем удерживается только остаток от деления полученного произведения на полином .

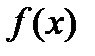Отметим, что среди полиномов степени не выше 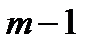присутствуют и полиномы нулевой степени, т.е. элементы простого поля 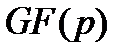, сложение и умножение которых, осуществляются по правилам 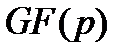. Это означает, что простое поле 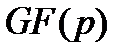полностью содержится в расширенном 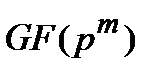, или, другими словами, 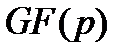является подполем 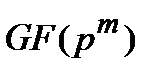. Для поля 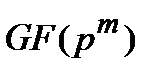порядок его простого подполя 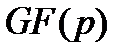называется характеристикой поля 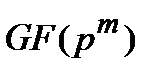. Например,любое расширенное поле 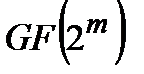является полем характеристики 2, вследствие чего вычисление коэффициентов полиномов, рассматриваемых как элементы поля 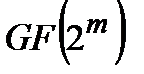, осуществляется по модулю два. В частности, для любого 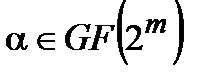, , 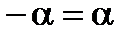поскольку .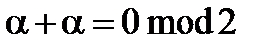