Обычно 3-х значные цифры не пишутся поэтому не 106.5 а 06.5

11.Ищем время (∆t-промежуток времени который прошел)∆t=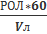

12.Теперь ищем траверзное время -tтрав.=t1(время в нач. точке) + ∆t

13.-Ищем ГКП траверзное (от точки на Пус куда проводили перп. с вышки) можем получить только ИП поэтому переводим в ГКП=Ип-∆ГК -Dтравер. –Путевую скорость (от начала до «вектора обратного течения на Пус)

Обратная задачаодновременный учет дрейфа и течения

-Дан Пус и нужно найти ГКК

Из произвольной точки прокладываем Пус

2.находим относительную скорость Vо=Vлаг.*коэф. лага.

Из начальной точки проводим вектор течения по направлению и скорости.

Из конца вектора течения мы делаем засечку на Пус по V0

5.С помощью параллельной линейки совмещаем конец вектора и нашу засечку и переносим параллельно эту линию в начальную точку. Получили Пуα. Теперь измеряем этот курс, считаем β=Пус-Пуα и работаем с ветром Ик=Пуα-α и рисуем полученный ИК. Так же находим суммарный снос.

6.Наносим буровую вышку изменив пеленг. Из этой точки проводим перпендикуляр к Пус и из полученной точки линию к концу вектора течения (получили точку x) Эту точку мы проводим в обратную сторону течения до пересечения с Пуα. Снимаем эту величину и получим S

7.Считаем Рол= Находим ол траверза ол1=Ол2+РОЛ. После считаем затраченное время ∆t= 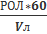и находим tтраверз

Из точки x (куда провели перпендикуляр от вышки) снимаем ИП и переводим в ГКП. –Находим D -Находим путевую скорость (от нач. точки до x)

Аналитическое счисление пути судна и его точность.

Аналитическое счисление

Учет перемещения судна можно осуществлять не только графическими построениями на карте, но и путем выполнения расчетов по формулам аналитическим методом.

Аналитическое, или письменное, счисление применяется: при океанских переходах, когда отсутствуют крупномасштабные карты; при решении астрономических задач по определению места судна по Солнцу; во всех случаях, когда по какой-либо причине ведение графического счисления затруднено.

Сущность способа заключается в определении конечных координат судна по известным начальным координатам и их приращениям, рассчитанным по формулам

φ2 - φ1 = РШ

λ2 - λ1 = РД.

Выведем зависимость РШ и РД от истинного курса судна и плавания по нему.

Предположим, судно совершило переход из пункта отхода A (φ1, λ1) в пункт прихода В(φ2, λ2) постоянным курсом К, пройдя расстояние S (рис. 57).

Разделим расстояние между пунктами A и B на большое число равных элементарных отрезков ΔS. Через полученные точки проведем меридианы и отрезки параллелей. В результате построения получим равные элементарные прямоугольные треугольники, которые по малости их можем рассматривать как плоские. Для удобства вывода формул Землю примем за шар.

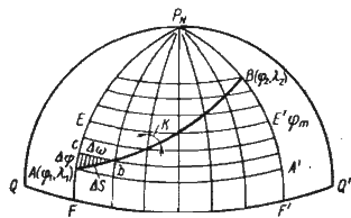Рассмотрим элементарный прямоугольный треугольник Abc. Гипотенуза тругольника Аb представляет собой отрезок локсодромии ΔS. Катет Aс является отрезком меридиана и представляет собой элементарную разность широт Δφ. Катет cb представляет собой элементарное расстояние по параллели между меридианами точек А и b,называемое элементарным отшест-вием Aw.

На основании формул плоской тригонометрии из треугольника Abc можно выразить катет Ас: Δф = ΔS cos К.

Далее для расчета широты или долготы можно использовать формулы но проще будет использовать таблицы составлена таблица 24 «Разность широт и отшествие» в МТ — 75. Аргументами для входа в таблицу служат ИК и плавание S, выбираются — РШ и ОТШ.

А для отшествия Таблица 25а МТ — 75 составлена по формуле (85) и служит для выбора разности долгот по отшествию и средней широте.