Дайтс определение и выведите формулу периода колебаний математического маятника.
43. Дайте определение и выведите формулу периода колебаний физического маятника.
В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.
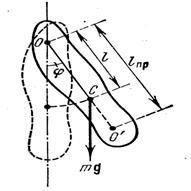 |
Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении от положения равновесия на угол 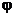 возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен:
возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен:



 ,
,
 где m – масса маятника, l – расстояние между точкой подвеса О и центром инерции C маятника. Знак “ – ” имеет тоже значение, что и в случае квазиупругой силы
где m – масса маятника, l – расстояние между точкой подвеса О и центром инерции C маятника. Знак “ – ” имеет тоже значение, что и в случае квазиупругой силы 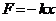 . Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать основной закон динамики:
. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать основной закон динамики:

В случае малых колебаний это уравнение переходит в уже известное нам уравнение незатухающих гармонических колебаний:
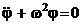 ,
,
где через  обозначена в данном случае следующая величина:
обозначена в данном случае следующая величина:
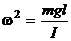
Из этого уравнения следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания. При этом период колебаний физического маятника определяется выражением:

Проведенное выше рассмотрение имеет место и для математического маятника. В этом случае маятник представляет собой материальную точку, момент инерции которой относительно оси, проходящей через точку подвеса, равен  . С учетом этого, получаем формулу для периода колебаний математического маятника:
. С учетом этого, получаем формулу для периода колебаний математического маятника:

Для физического маятника вводится понятие приведенной длины 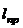 . Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника, т.е.
. Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника, т.е. 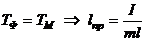 .
.
Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку 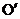 на рисунке). Можно показать, что при подвешивании маятника в центре качания
на рисунке). Можно показать, что при подвешивании маятника в центре качания 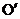 приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания точка подвеса становится новым центром качания.
приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания точка подвеса становится новым центром качания.
Получите дифференциальное уравнение затухающих гармонических колебаний.
45. По какому закону изменяется колеблющаяся величина при затухающих гармонических колебаниях? Приведите график зависимости
