Построение моделей пространства состояний с внутренним шумом

9.8. Алгоритм совместного оценивания элементов векторов 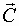и

ПОНЯТИЕ МОДЕЛЕЙ ПРОСТРАНСТВА СОСТОЯНИЙ.

Модель пространства состояний - динамическая модель, которая связывает между собой три группы переменных:

1. входные переменные объекта управления;

2. переменные состояния объекта управления;

3. выходные переменные объекта управления.

Переменные состояния объекта управления - это дополнительные переменные, использование которых позволяет зависимость не только выходной переменной от входной, но и некоторые функции выходной переменной от входной.

Число переменных состояния равно порядку дифференциального уравнения описывающего объект управления.

Частным случаем переменных состояния являются фазовые координаты, то есть производные выходного сигнала.

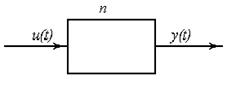
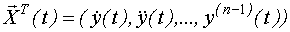- вектор состояния или вектор фазовых переменных.

В дальнейшем будем рассматривать дискретные модели пространства состояний.

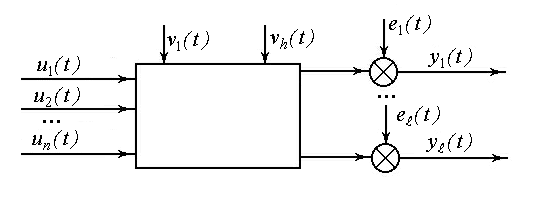
НЕПРЕРЫВНАЯ ФОРМА МОДЕЛИ ПРОСТРАНСТВА СОСТОЯНИЙ.

В непрерывной форме модель пространства состояний в общем случае и имеет вид:

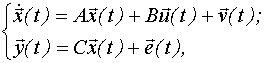
где 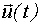- k-мерный вектор входных воздействий;

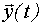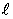- -мерный вектор выходных воздействий;

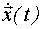- n-мерный вектор пространства состояний;

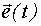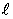- -мерный вектор внешнего шума;

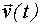- n-мерный вектор внутреннего шума;

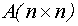- матрица состояний;

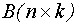- матрица управления;

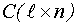- матрица наблюдений.

ДИСКРЕТНАЯ МОДЕЛЬ ПРОСТРАНСТВА СОСТОЯНИЙ.

В дальнейшем будем использовать дискретные модели пространства состояний, которые для одномерных систем имеют вид:

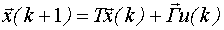- уравнение состояния,

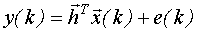- уравнение наблюдения,

где 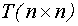- матрица состояний;

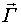- n-мерный вектор управления;

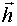- n-мерный вектор наблюдений;

k - дискретное время.

В дискретной модели роль первой производной выполняет первая разность .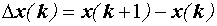

Аналогом второй производной является вторая разность

.

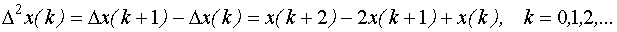Если переменными состояния являются фазовые координаты, товектор наблюдений 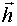имеет вид:

.

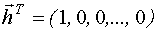В этом случае неизвестными параметрами являются матрица T и вектор 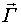, число неизвестных параметров: .

Чтобы уменьшить число неизвестных параметров обычно используется каноническая форма модели пространства состояний. В соответствии с этой формой T имеет вид:

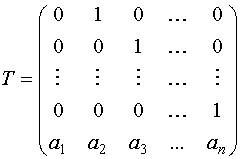
Каноническая структура содержит 2n неизвестных параметров. Вектор неизвестных параметров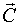

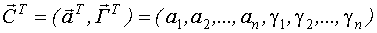
ПРИВЕДЕНИЕ МОДЕЛИ ПРОСТРАНСТВА СОСТОЯНИЙ К ДИНАМИЧЕСКОЙ РЕГРЕССИОННОЙ МОДЕЛИ ТИПА "ВХОД-ВЫХОД".

Если начальные условия объекта управления нулевые, то есть при 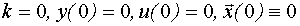, то модель пространства состояний может быть сведена к динамической регрессионной модели типа ⌠вход √ выход■.

Поскольку все реальные объекты функционируют не при нулевых начальных условиях, то при их описании динамическими регрессионными моделями необходимо в качестве переменных использовать их отклонения от исходного статического состояния, то есть состояния, в котором находится объект до начала его исследования. При этом необходимо, чтобы до начала исследований объект управления находился в статическом состоянии хотя бы в течение времени памяти объекта управления, то есть переменные должны быть постоянными.

Выведем структуру динамической регрессионной модели эквивалентной модели пространства состояний при нулевых начальных условиях:

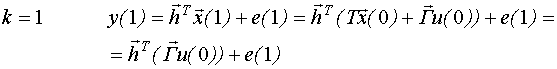
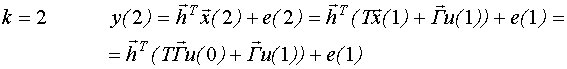
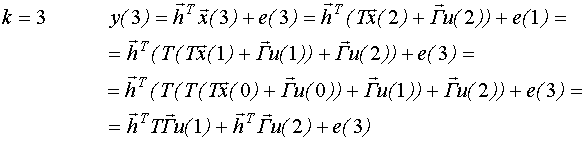
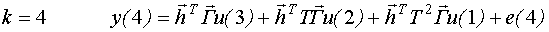
Таким образом, мы получили модель типа ⌠вход-выход■, которую можно записать следующим образом:

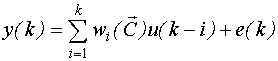- дискретная модель свертки,

где 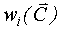- i-ая ордината импульсной переходной функции, определяемая следующим матричным выражением: .

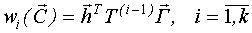i-ая ордината импульсной переходной функции однозначно определяется значениями параметров матрицыT и вектора 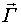модели пространствасостояний, то есть она является функцией вектора 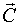и является сильно нелинейной.

Таким образом, получена модель типа ⌠вход √ выход■, неизвестными параметрами которой являются неизвестные параметры модели пространства состояний. Получив такую модель по изменениям входа и выхода, мы получим искомую модель пространства состояний.

Полученная структура динамической регрессионной модели является нелинейно-параметризованной по всем неизвестным параметрам.

СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ВЕКТОРА НЕИЗВЕСТНЫХ ПАРАМЕТРОВ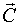
И ОРДИНАТАМИ ИМПУЛЬСНОЙ ПЕРЕХОДНОЙ ФУНКЦИИ.

Для получения оценки вектора неизвестных параметров необходимо использовать методы нелинейного оценивания. При нахождении начального приближения необходимо использовать соответствия между элементами вектора 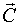и ординатами импульсной переходной функции, таким образом, процедура нелинейного оценивания должна реализовываться в следующей последовательности:

1. определение методом наименьших квадратов оценок ординат импульсной переходной функции;

2. вычисление неизвестных коэффициентов модели пространства состояний по оценкам ординат импульсной переходной функции с использованием соответствующих соответствий, найденные оценки принимаются в качестве начальной оценки вектора ;

3. нахождение НМНК-оценки вектора неизвестных параметров методом Гаусса-Ньютона.

Такой подход позволяет обеспечить достаточно высокую точность начального приближения вектора неизвестных параметров, что необходимо для обеспечения сходимости метода Гаусса-Ньютона, и уточнить структуру модели пространства состояний (порядок системы) после решения первого этапа по виду импульсной переходной функции.

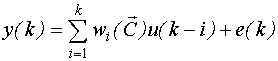
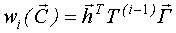
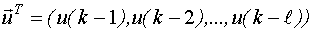
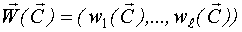
Получим соответствие между элементами вектора неизвестных параметров и ординатами импульсной переходной функции:

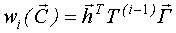
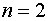
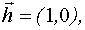
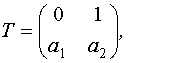
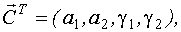
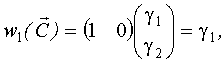
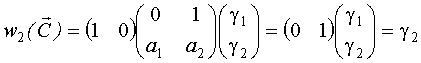
Таким образом, первые n ординат импульсной переходной функции равны

соответствующим элементам вектора .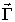

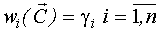(1)

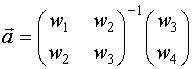
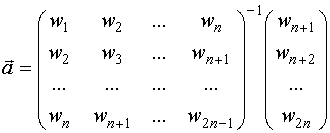(2)

Использование полученных соотношений (1) и (2) корректно только в части вычисления оценок вектора 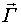. Точность оценок матрицы 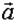зависит от оценки вектора 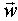. Если ординаты импульсной переходной функции вычислены неточно, то задача может стать некорректной, что следует из необходимости обращения матрицы 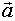, которая может быть плохо обусловлена. Поэтому это соответствие можно использовать либо в детерминированном случае, либо при вычислении начального приближения вектора неизвестных параметров 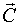в задаче нелинейного оценивания.

ВЫЧИСЛЕНИЕ НМНК-ОЦЕНОК ЭЛЕМЕНТОВ ВЕКТОРА
НЕИЗВЕСТНЫХ ПАРАМЕТРОВ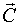

Разложим функцию регрессии в ряд Тейлора в окрестностях точки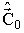

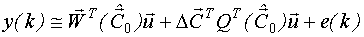
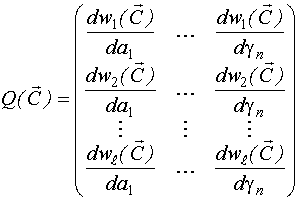
Матрица 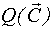может быть вычислена по общему алгоритму.

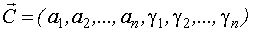
Пусть n=2

I строка 0 0 1 0

II строка 0 0 1 0

Первые n строк матрицы 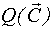представляют собой блочную матрицу, состоящую из двух квадратных матриц размерностью n*n:

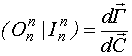
где 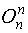- нулевая матрица;

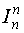- единичная матрица.

Найдем n+1 строку

III строка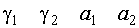

IV строка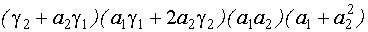

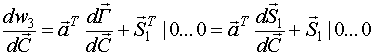
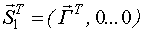
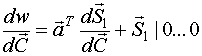
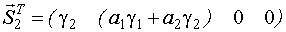
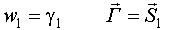
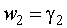
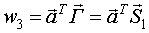
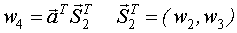
Тогда, в общем виде: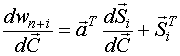

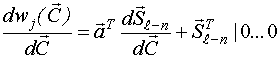
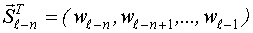
НМНК-оценка вектора неизвестных параметров вычисляется методом Гаусса-Нъютона по следующей итерационной формуле:

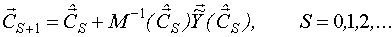
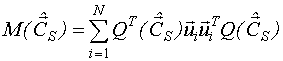
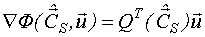
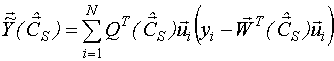
ПОСТРОЕНИЕ МОДЕЛЕЙ ПРСТРАНСТВА СОСТОЯНИЙ
С ВНУТРЕННИМ ШУМОМ.

Рассмотрим одномерную дискретную систему, описываемую моделью пространства состояний вида

где 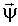- вектор неизвестных параметров;

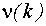- дискретный внутренний шум системы.

В этом случае неизвестны элементы векторов 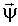и .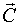

Модель пространства состояний с внутренним шумом при нулевых начальных условиях также можно свести к динамической регрессионной модели типа ⌠вход-выход■.

,

,

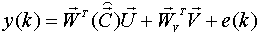
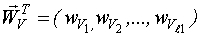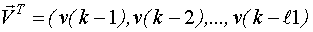где 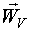- вектор ординат импульсной переходной функции по каналу внутренний шум - выход;

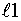- дискретное время памяти по каналу внутренний шум - выход;

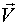- вектор предыстории по внутреннему шуму.

Поскольку внутренний шум не может быть измерен, полученную модель ⌠вход - выход■ непосредственно для оценивания векторов и 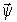использоватьнельзя. Для оценивания параметров модели пространства состояний с внутренним шумом можно использовать следующий подход:

Обозначим 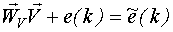, с учетом того, что 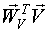и e(k) являются случайными функциями времени, их можно объединить в 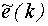. Представим процесс 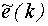как выход некоторой линейной динамической системы, на вход которой подается чисто случайный процесс 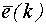- белый шум.

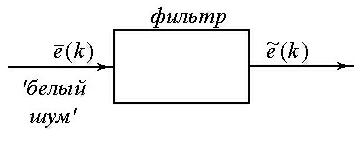
Таким образом, при таком представлении модели, ее неизвестными параметрами являются элементы вектора 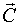и неизвестные параметры фильтра, преобразующего ⌠белый шум■ в процесс 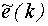. При этом, обычно модель фильтра задают в виде его дискретной передаточной функции 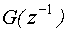, структура которой задается априори.

,

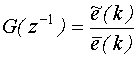где z √ оператор сдвига на число разрядов дискретного времени, равное степени z, то есть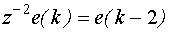

Таким образом, задача свелась к задаче оценивания вектора 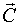и неизвестных коэффициентов дискретной передаточной функции.

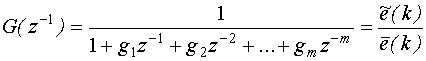
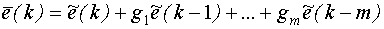
Окончательно мы получили вектор неизвестных параметров

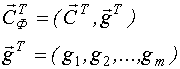
Модель 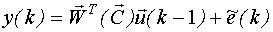обычно представляется следующим образом:

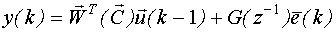
Умножим левую и правую часть на 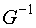и получим:

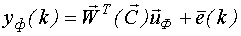
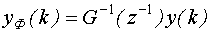
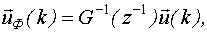
где 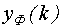- отфильтрованное значение выхода;

- отфильтрованный вектор предыстории по входу.

Таким образом, относительно отфильтрованных значений полученная модель совпадает с моделью без внутреннего шума, при условии, что внешний шум является белым шумом.

АЛГОРИТМ СОВМЕСТНОГО ОЦЕНИВАНИЯ ЭЛЕМЕНТОВ
ВЕКТОРОВ 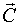И .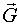

Алгоритм является итерационным и реализуется в следующей последовательности:

1. На основе результатов эксперимента (то есть измерений значений входных и выходных переменных) вычисляется НМНК - оценка вектора 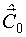без учета внутреннего шума.

2. Вычисляется вектор невязок

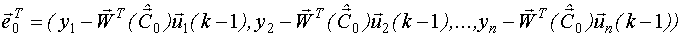- вектор отклонений экспериментальных значений от нашей модели. При этом принимается полученное значение невязок в качестве оценок .

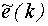3. Методом наименьших квадратов вычисляется начальная оценка вектора параметров фильтра .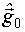

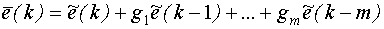
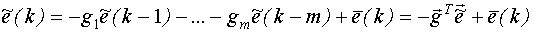
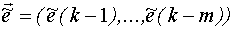
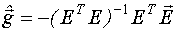
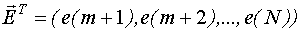
4. Фильтрация значений входных 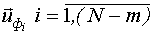и выходных 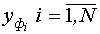переменных:

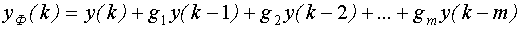
5. Вычисление НМНК - оценки вектора 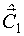по процедуре Гаусса-Ньютона с заменой значений входных и выходных переменных на отфильтрованные.

6. Вычисление 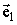и так далее.

Процедура заканчивается тогда, когда 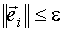(- заданное малое число).

Тема 10. Основы теории планирования эксперимента

10.1. Основные идеи планирования эксперимента

10.2. Основные понятия и определения теории планирования эксперимента

10.2.1. Факторы планирования

10.2.2. Пространство планирования

План эксперимента

10.2.4. Критерии оптимальности планов и моделей

ОСНОВНЫЕ ИДЕИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА.

Пусть имеется объект,

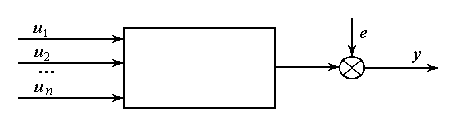
структура модели которого является линейно-параметризованной.

МНК-оценка вектора неизвестных коэфициентов:

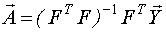
Качество модели характеризуется ковариационной матрицей .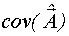

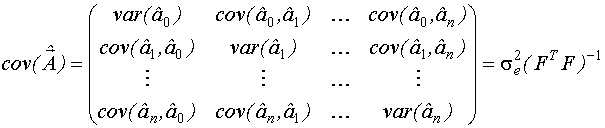
В случае линейной параметризации модели информационная матрица определяется на основе измерений входных переменных объекта (то есть информационная матрица определяется матрицей входных переменных ) и не зависит от значений выхода, полученных по результатам эксперимента.

В случае линейной параметризации модели имеется возможность так спланировать эксперимент, то есть определить такую матрицу входных переменных, при которой ковариационная матрица оценок неизвестных параметров обладает теми или иными желаемыми свойствами. В пассивном эксперименте, когда матрица входных переменных является во многом случайной, ковариационная матрица оценок чаще всего является плохо обусловленной (то есть ее детерминант близок к нулю), поэтому планирование эксперимента, то есть активное экспериментирование, когда входные переменные не просто измеряются, а устанавливаются на некоторых оптимальных уровнях, позволяет получить модели, обладающие теми или иными оптимальными свойствами.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

ТЕОРИИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА.

Факторы планирования.

Факторами планирования будем называть управляемые входные переменные

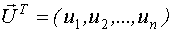
Пространство планирования.

Пространство планирования 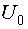- это область в n-мерном пространстве, внутри и на границах которой можно проводить опыты. Область планирования может быть правильной и произвольной формы.

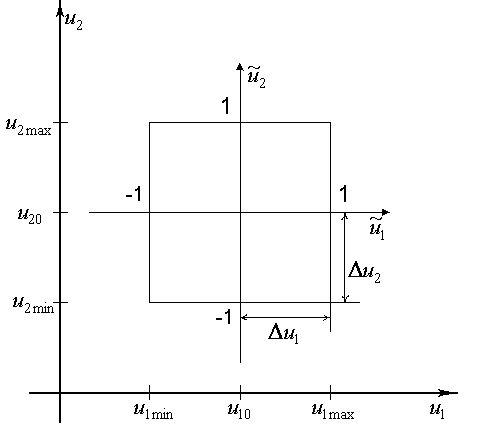
Обычно факторы планирования нормируют следующим образом:

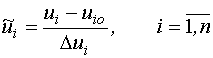
- координата центра области планирования;

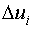- половина интервала планирования.

Нормированное пространство планирования (пространство планирования для нормированных факторов) представляет собой единичный n-мерный гиперкуб.

На этапе планирования эксперимента обычно используются нормированные факторы, а на этапе обработки результатов эксперимента вначале получают модель для нормированных факторов, а затем осуществляют переход к исходным факторам путем замены нормированных факторов их выражениями.

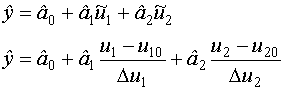
Большинство известных планов предполагают, что областью планирования являются либо единичный n-мерный гиперкуб, либо единичная гиперсфера.

План эксперимента.

План эксперимента ( ) - это совокупность точек пространства планирования, в которых производятся опыты.
План эксперимента задается спектром плана и частотами повторений наблюдений в точках спектра.

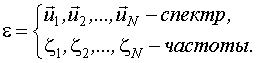
Спектр ("скелет плана") - это совокупность неповторяющихся точек пространства планирования, в которых производятся опыты.

Частота повторения наблюдений в i-ой точке определяется:

,

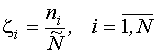где 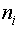- число опытов в i-ой точке спектра;

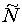- общее число опытов, предусмотренных планом;

Планы делятся на точные и непрерывные.

План называется точным, если в нем все точно известно, то есть общее число опытов и число опытов в i-ой точке плана известны и являются целымивеличинами.

План называется непрерывным или асимптотическим, если для заданного значения общего числа опытов не все значения числа опытов в i-ой точке являются целыми величинами. Если для данного значения числа опытов план не является точным, то его необходимо округлить до ближайшего точного плана при том же общем числе опытов, либо изменить общее число опытов.

Критерии оптимальности планов и моделей.

Каждый план и полученная на его основе регрессионная модель должны удовлетворять соответствующему критерию оптимальности.

Критерии оптимальности делятся на две группы. К первой группе относятся критерии, характеризующие точность оценок неизвестных параметров модели; ко второй √ критерии, характеризующие предсказательные свойства, полученной на основе плана модели регрессии.

Первая группа:

1) критерий ортогональности,

2) D-оптимальность,

3) A-оптимальность и т.д.

Вторая группа:

1) рототабельность,

2) G-оптимальность,

3) Q-оптимальность и т.д.

Критерий ортогональности.

План называется ортогональным, если соответствующая ему ковариационная матрица оценок параметров модели диагональная:

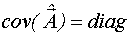
Ортогональный план обеспечивает некоррелированность МНК - оценок неизвестных параметров модели.

D-оптимальность.

План называется D-оптимальным, если он минимизирует определитель ковариационной матрицы оценок, то есть:

Критерий D-оптимальности обеспечивает минимизацию объема эллипсоида рассеивания оценок параметров модели или обобщенную дисперсию оценок.

Пусть имеется модель

В результате многократного повторения идентификации получим точки, попадающие в область, ограниченную эллипсом рассеивания.

Внутри эллипса находится точка с координатами равными истинным значениям неизвестных параметров модели.

Объем эллипсоида рассеивания прямо пропорционален определителю ковариационной матрицы.

А-оптимальность.

План называется А-оптимальным, если он минимизирует след ковариационной матрицы оценок неизвестных параметров

Этот критерий минимизирует сумму дисперсий оценок неизвестных параметров.

Недостаток данного критерия состоит в том, что он не учитывает коррелированность оценок неизвестных параметров.

Вторую группу критериев оптимальности составляют критерии, обеспечивающие те или иные свойства дисперсионной функции регрессионной модели, то есть функции, определяющей зависимость дисперсии предсказания выхода по модели от координат точки предсказания.

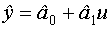
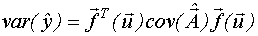- дисперсионная функция

Рототабельность.

План называется рототабельным, если дисперсия предсказания выхода по соответствующей ему модели зависит только от расстояния точки предсказания от центра области планирования и не зависит от направления предсказания, то есть в точках равноудаленных от центра области планирования дисперсия предсказания одинакова.

Критерий рототабельности удобен, если получаемая регрессионная модель используется при статической оптимизации параметров или режимов объектов. При этом предполагается, что оптимизация осуществляется поисковыми методами.

G-оптимальность.

План называется G-оптимальным или минимаксным, если он минимизирует максимальную по пространству планирования дисперсию предсказания выхода.

Максимальная дисперсия должна быть минимальна по пространству планирования.

Существует теорема эквивалентности, согласно которой для линейно-параметризованных моделей критерии D- и G-оптимальности эквивалентны. То есть D-оптимальный план является G-оптимальным инаоборот.

Q-оптимальность.

План называется Q-оптимальным, если он минимизирует среднюю по пространству планирования дисперсию предсказания выхода.

Тема 11. Ортогональные планы первого порядка

11.1. Назначение и типы ортогональных планов первого порядка

11.2. Полный факторный эксперимент (ПФЭ, )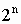

11.3. Вычисление МНК-оценок и их свойства при ортогональном планировании первого порядка.