Экспериментальные статистические методы моделирования
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
Тема 1. Введение
Типы математических моделей
Представление объекта управления в реальных условиях эксплуатации
ТИПЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
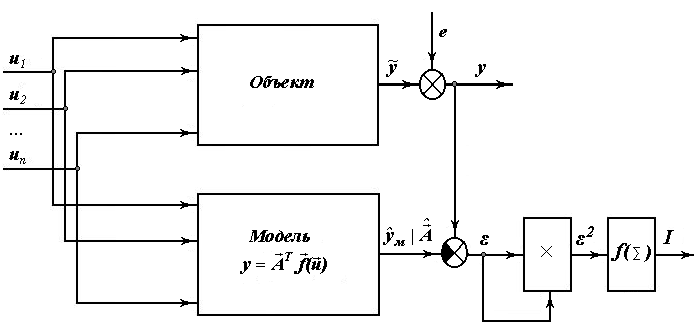
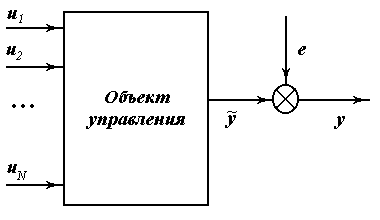
Любая система состоит из объекта управления и управляющего устройства и может быть представлена в виде следующей схемы.

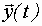 - выходная координата
- выходная координата
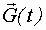 - задающее воздействие
- задающее воздействие
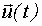 - управляющее воздействие
- управляющее воздействие
Целью управления является обеспечение равенства  .
.
В реальных условиях объект управления подвергается воздействиям случайных помех, для обработки которых и предназначена система управления.
Целью математического моделирования является определение системы уравнений, связывающей входные и выходные переменные объекта управления. Получить такую систему уравнений можно двумя способами: аналитическим и используя экспериментально-статистические методы.
Аналитический метод предполагает изучение процессов, происходящих в объекте управления, и описание их на основе соответствующей отрасли науки. Его недостатком является невозможность качественного моделирования объектов управления, фу нкционирующих в реальных условиях.
Экспериментально-статистические методы позволяют моделировать объекты и системы, функционирующие в реальных условиях. В основе этих методов лежит эксперимент, обработка результатов которого осуществляется статистическими методами.
Экспериментально-статистические методы, как правило, предполагают, что структура математической модели известна с точностью до параметров, а основной целью этих методов является определение этих параметров.
Например.


Эксперимент заключается в измерении входных и выходных переменных. При этом эксперименты делятся на активные и пассивные.
Пассивный эксперимент заключается в измерении входных и выходных переменных в условиях нормальной эксплуатации.
Активный эксперимент заключается в изменении входных переменных по специальному плану.
Таким образом, моделирование объекта управления должно состоять из двух этапов:
1. определение структуры модели аналитическими методами;
2. определение параметров модели экспериментально - статистическими методами.
ПРЕДСТАВЛЕНИЕ ОБЪЕКТА УПРАВЛЕНИЯ
В РЕАЛЬНЫХ УСЛОВИЯХ ЭКСПЛУАТАЦИИ

Входные переменные можно разбить на три группы:
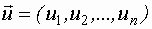 | - вектор управляемых и контролируемых входных переменных, которые можно измерять и изменять. Через эти переменные замыкается главная обратная связь системы управления, то есть ими управляет оператор. |
 | - вектор неуправляемых контролируемых переменных (измеряемые и неуправляемые). |
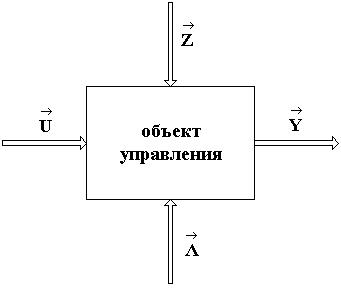
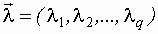 | - вектор неуправляемых и неконтролируемых выходных переменных. |
 | Переменные типа  - детерминированные переменные. Переменные типа - детерминированные переменные. Переменные типа  - случайные переменные, принимающие в каждом опыте различные значения. - случайные переменные, принимающие в каждом опыте различные значения. |
Математическая модель объекта управления представляет собой систему уравнений следующего вида:

Преобразование  может быть определено точно, если на объект управления не действуют случайные входные переменные. При наличии переменных типа
может быть определено точно, если на объект управления не действуют случайные входные переменные. При наличии переменных типа  речь идет о приближении (оценке) преобразования
речь идет о приближении (оценке) преобразования  .
.
Существуют три типа преобразований:
1. функция;
2. оператор;
3. функционал.

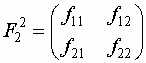 - матричная функция
- матричная функция
Модели объектов управления делятся на модели статики (статистические) и модели динамики (динамические).
Модели статики - это уравнения связывающие выход и вход в статистическом режиме объекта управления (после окончания переходного процесса).
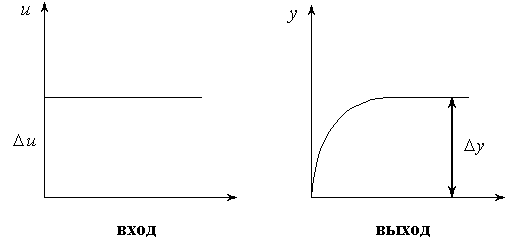
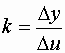 - коэффициент передачи.
- коэффициент передачи.
Статическая характеристика линейных объектов линейна: 
Модели статики могут быть линейно-параметризованными и нелинейно-параметризованными, то есть они могут быть линейными по неизвестным параметрам.

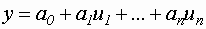 - линейная модель.
- линейная модель.
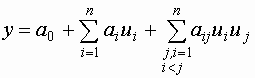 - линейная модель с парными взаимодействиями.
- линейная модель с парными взаимодействиями.
Рассмотрим объект с двумя входами и одним выходом: 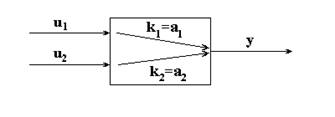
| Модель 1. |  , где , где 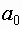 - свободная составляющая; - свободная составляющая;  - реакция на первый выход; - реакция на первый выход; 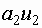 - реакция на второй выход. - реакция на второй выход. |
| Модель 2. | 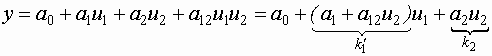 |
Парное взаимодействие входов 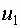 и
и 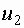 заключается в том, что коэффициент передачи по одному входу зависит от значения другого входа.
заключается в том, что коэффициент передачи по одному входу зависит от значения другого входа.
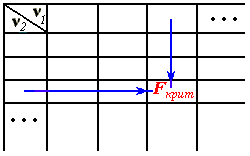
Для проверки наличия парного взаимодействия проводят эксперимент:
 , а , а 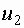 будет изменяться будет изменяться | 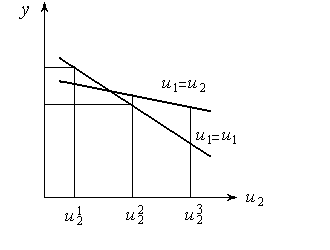 |
Если статическая характеристика по одному входу при различных значениях другого входа изменяет наклон, то взаимодействие входов имеет место, в противном случае взаимодействие отсутствует.
Для большинства объектов управления взаимодействия выше второго порядка практически равны нулю.
| Модель 3. | 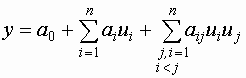 |
Рассмотрим пример, когда n=3:
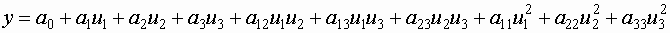 - полная квадратичная модель.
- полная квадратичная модель.
Рассмотренные модели являются линейными по неизвестным параметрам. Две последние модели нелинейны по входу (по структуре).
Модель линейна по данному коэффициенту, если частная производная по нему не зависит от остальных коэффициентов.
| Линейно-параметризованная модель может быть записана в виде скалярного произведения вектора неизвестных коэффициентов и вектора-функции базисных функций: | 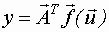 , , |
где
| для первой модели: |  |
| для второй модели: |  |
| Нелинейно-параметризованная модель - это модель, которую нельзя представить в виде скалярного произведения: | 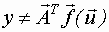 |
| Модель является нелинейно-параметризованной, если хотя бы один элемент входит в нее нелинейно. |  . . |
Свойства оценок
Свойства оценок
Оценки характеристик случайных величин, как и другие оценки, характеризуются следующими свойствами:
1. смещенность или несмещенность;
2. состоятельность или несостоятельность;
3. эффективность или неэффективность.
Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине
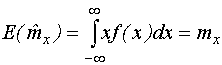
E - символ математического ожидания.
В противном случае оценка называется смещенной.
Оценка называется состоятельной, если выполняется следующее условие:
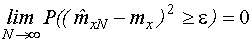
Свойство состоятельности заключается в том, что с ростом объема выборки точность оценки увеличивается.
Оценка называется эффективной, если ее дисперсия минимально возможная: 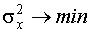
Регрессионных моделей
Метод наименьших квадратов
Метод наименьших квадратов
Этот метод применяется в основном в случае линейной параметризации.
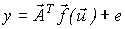
Найдем оценку вектора 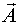 .
.
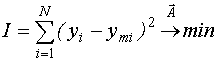 - запись экстремальной задачи.
- запись экстремальной задачи.
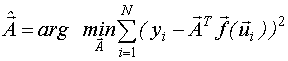 - запись аргументной задачи.
- запись аргументной задачи.
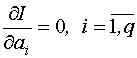
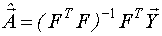 ,
,
где 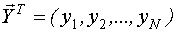 - вектор значений выхода объекта управления в N измерениях;
- вектор значений выхода объекта управления в N измерениях;
F - матрица базисных функций размерностью N*q.
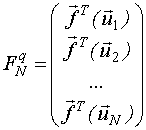
Пример.
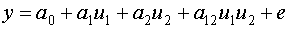
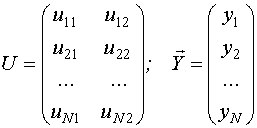
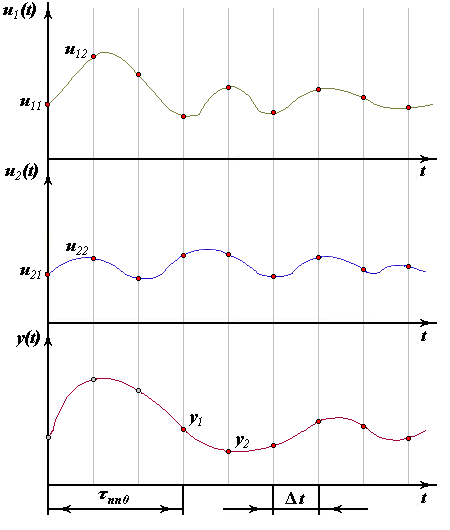
где 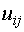 - значение i-го входа при j-ом измерении;
- значение i-го входа при j-ом измерении;
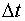 - шаг дискретизации.
- шаг дискретизации.
Выходной сигнал снимается через время переходного процесса после изменения значений входов.
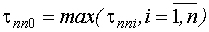 - время переходного процесса.
- время переходного процесса.
Для определения времени переходного процесса необходимо определить время переходного процесса каждого канала, для чего подать поочередно на каждый вход ступенчатое воздействие при стабильных остальных входах.
Время наблюдения выхода больше времени наблюдения входа.
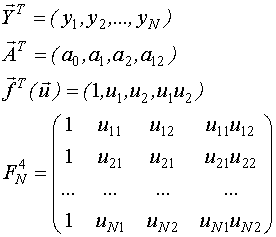
Ковариационная матрица оценок вектора 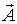 равна:
равна: 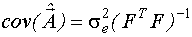
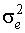 - дисперсия внешнего шума.
- дисперсия внешнего шума.
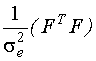 - информационная матрица Фишера.
- информационная матрица Фишера.
Характерно, что информационная матрица Фишера и ковариационная матрица оценок зависят только от входа объекта управления и не зависят от выхода, то есть они однозначно определяются значениями входных переменных и не зависят от значений выходных переменных.
Ковариационную матрицу точно вычислить невозможно, так как неизвестна дисперсия внешнего шума, но если оценить дисперсию внешнего шума, то можно найти оценку ковариационной матрицы.
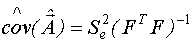
Уравнение, полученное в результате применения метода наименьших квадратов, называется уравнением регрессии.
Регрессия - это условное математическое ожидание или зависимость математического ожидания выходного параметра объекта от входных детерминированных переменных.
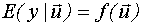
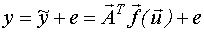
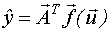 - уравнение регрессии
- уравнение регрессии
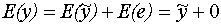
Так как E(e)=0 (e - центрированная случайная величина)
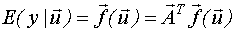
Структура уравнения регрессии совпадает с описанием объекта, когда случайная величина e(t) имеет нулевое математическое ожидание. В результате эксперимента можно найти лишь оценку уравнения регрессии 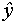 - предсказанное по уравнению регрессии значение выхода, которое является случайной величиной и зависит от вектора входных параметров
- предсказанное по уравнению регрессии значение выхода, которое является случайной величиной и зависит от вектора входных параметров 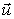 .
.
Математическое ожидание 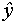 :
: 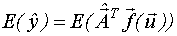
Пример.
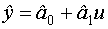
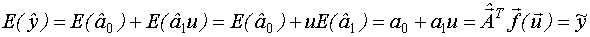
- если оценки неизвестных коэффициентов несмещены.
Дисперсия предсказания значений выхода имеет следующий вид: 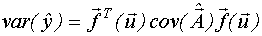
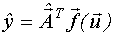 - дисперсионная функция модели регрессии.
- дисперсионная функция модели регрессии.
Дисперсионная функция позволяет оценить точность предсказания выхода по модели при различных значениях входных переменных.
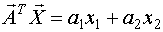 - линейная форма
- линейная форма
при 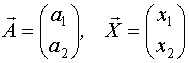
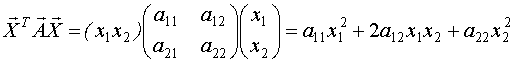 - квадратичная формa.
- квадратичная формa.
Корреляционная функция случайного процесса и ее свойства
Пусть x(t) - случайный процесс.
Автокорреляционной функцией случайного процесса x(t) называется функция
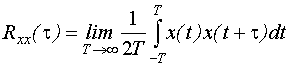
Случайный процесс-это функция, значения которой в каждый фиксированный момент времени являются случайными величинами.
Случайные процессы могут быть эргодическими и неэргодическими.
Процесс называется эргодическим, если его моментные характеристики, полученные по одной реализации, совпадают с теми же характеристиками, полученными по ансамблю реализаций. Таким образом, если процесс эргодический, то оценки математического ожидания и дисперсии этого процесса, полученные по одной бесконечно длинной реализации и по любому сечению бесконечно большого ансамбля реализаций, будут совпадать. Свойство эргодичности может иметь место только для стационарных случайных процессов.
| Процесс называется стационарным, если его математическое ожидание и дисперсия не зависят от времени. | 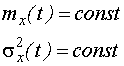 |
Если математическое ожидание и дисперсия случайного процесса зависят от времени, то процесс называется нестационарным.
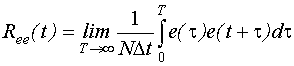
Для вычисления корреляционной функции случайного процесса необходимо иметь бесконечно длинную реализацию этого процесса. На практике может быть найдена лишь оценка автокорреляционной функции, так как реализация ограничена.

Для получения реализации случайного процесса необходимо провести следующий эксперимент: при стабильном входе зафиксировать значение выхода, далее необходимо определить математическое ожидание выходной переменной.
Реализация случайного процесса получается вычитанием из реализации выходного процесса математического ожидания выходного процесса.
На практике вычисляются ординаты оценки автокорреляционной функции по следующей формуле:
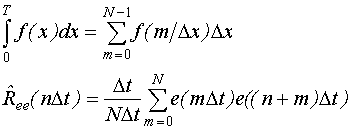
Данная формула пригодна в том случае, если автокорреляционная функция случайного процесса e(t) определяется не на основе всех имеющихся отсчетов процесса e(t), а на основе части этих отсчетов. В качестве "хвоста" можно использовать столько точек, сколько координат автокорреляционной функции мы хотим вычислить. Обычно число вычисляемых ординат должно быть в 2-3 раза больше дискретного времени памяти объекта: 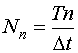 .
.
В этом случае в обработке участвуют все ординаты участка e(t). Недостатком этой формулы является то, что оценки ординат автокорреляционной функции вычисляется по выборкам различных объемов. Соответственно точность уменьшается с увеличением номера ординаты.
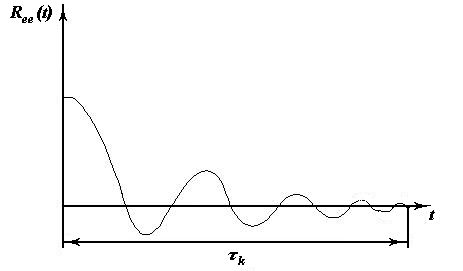
Получив оценку автокорреляционной функции, можно найти время корреляции случайного процесса e(t) - 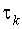 .
.
Время корреляции 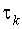 - это время затухания автокорреляционной функции до достаточно малой величины.
- это время затухания автокорреляционной функции до достаточно малой величины.
Наша функция не должна выходить за пределы ограничений и тогда определяется 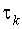
Метод наименьших квадратов применим, если измерение времени выхода происходит с интервалом не меньше времени корреляции ( 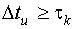 ).
).
Таким образом, последовательность выбора метода оценивания в случае непрерывной реализации входа-выхода должна быть следующей:
1. находится время корреляции;
2. задается структура модели и определяется число неизвестных коэффициентов(q);
3. определяется минимально необходимое число измерений (N) из условия 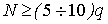 ;
;
4. определяется 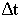 - интервал съема данных из условия
- интервал съема данных из условия 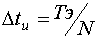 ;
;
5. правило выбора: если 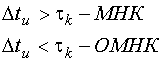
ОМНК при малых выборках
Если число измерений N не велико, то 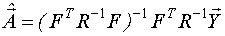 .
.
R- это ковариационная матрица измерений размерностью (N*N), то есть квадратная матрица.
 является случайным вектором.
является случайным вектором.
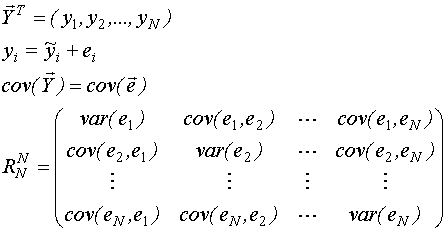
Матрицу R можно определить на основе оценки автокорреляционной функции случайного процесса e(t).
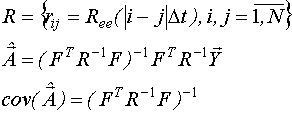
Такие оценки называются Марковскими. Они являются общим случаем оценок, частным случаем которых являются МНК оценка.
Если измерения не коррелированны между собой, то R будет иметь вид:
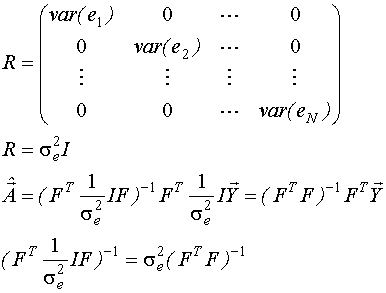
Главным недостатком Марковских оценок является обращение матрицы R, что возможно при небольшом числе измерений.
Проверка значимости
Проверка адекватности
Проверка значимости.
Имеем 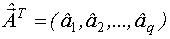 - оценки соответствующих коэффициентов.
- оценки соответствующих коэффициентов.
Мы должны проверить (оценить) коэффициенты 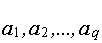 на их отличие от нуля.
на их отличие от нуля.
Проверка значимости i-ого коэффициента модели эквивалентна проверке гипотезы о том, что 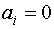 (нуль-гипотеза). Исходными данными этой гипотезы являются оценка коэффициентов и дисперсия (точность) оценки. Проверка гипотезы сводится к использованию статистики с известным законом распределения.
(нуль-гипотеза). Исходными данными этой гипотезы являются оценка коэффициентов и дисперсия (точность) оценки. Проверка гипотезы сводится к использованию статистики с известным законом распределения.
Статистикой называют некоторое выражение, построенное на известных оценочных характеристиках.
Известно, что отношение модуля оценки к корню квадратному из оценки дисперсии называется t-распределением (Стьюдента).
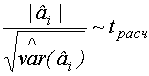
Нуль-гипотеза принимается, если отношение 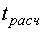 меньше некоторого критического значения
меньше некоторого критического значения 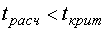 . Если неравенство не выполняется, то нуль-гипотеза отвергается.
. Если неравенство не выполняется, то нуль-гипотеза отвергается.
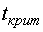 - это квантиль распределения Стьюдента, соответствующий уровню значимости
- это квантиль распределения Стьюдента, соответствующий уровню значимости 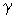 и числу степеней свободы
и числу степеней свободы 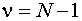 .
.
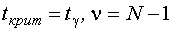 .
.
Квантиль - это значение случайной величины, соответствующее заданной вероятности.
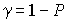 , где Р- доверительная вероятность, то есть вероятность, с которой принимается нуль-гипотеза при выполнении нашего неравенства
, где Р- доверительная вероятность, то есть вероятность, с которой принимается нуль-гипотеза при выполнении нашего неравенства 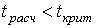 . Обычно
. Обычно 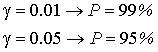
Квантили определяются по справочнику следующим образом:
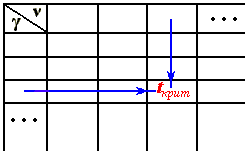
После проверки значимости все незначащие коэффициенты исключаются из модели. Таким образом осуществляется корректировка структуры модели.
Проверка адекватности.
Проверка адекватности сводится к проверке гипотезы о равенстве дисперсии адекватности и дисперсии внешнего шума: 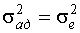 .
.
Дисперсия адекватности характеризует точность предсказания выхода по модели, то есть это дисперсия случайной величины, которая является разностью между экспериментальным значением выхода и значением выхода, рассчитанным по модели.
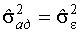
1. 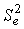 -оценка дисперсии внешнего шума.
-оценка дисперсии внешнего шума.
2. 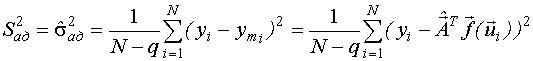
Отношение 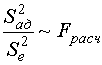 - F-распределение (по закону Фишера)
- F-распределение (по закону Фишера)
Если выполняется неравенство 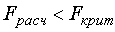 , то модель признается адекватной экспериментальным данным. В противном случае, модель не адекватна, то есть структура модели выбрана неверно. Ее необходимо изменить и для новой структуры провести все исследование.
, то модель признается адекватной экспериментальным данным. В противном случае, модель не адекватна, то есть структура модели выбрана неверно. Ее необходимо изменить и для новой структуры провести все исследование.
Квантиль ( 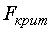 ) должен удовлетворять трем условиям
) должен удовлетворять трем условиям 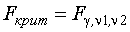 ,
,
где 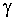 -уровень значимости;
-уровень значимости;
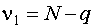 - число степеней свободы числителя дисперсионного отношения;
- число степеней свободы числителя дисперсионного отношения;
 - число степеней свободы знаменателя дисперсионного отношения.
- число степеней свободы знаменателя дисперсионного отношения.
Для определения 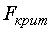 используется справочник, но предварительно выбирается конкретное значение
используется справочник, но предварительно выбирается конкретное значение 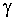 .
.
Метод Гаусса-Ньютона
Метод Хартли
Метод Марквардта
Метод Гаусса-Ньютона
Имеется модель 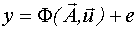
Задается исходное начальное приближение 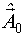 .
.
Функция регрессии раскладывается в ряд Тейлора в окрестности начального приближения, при этом в разложении используют только свободные член и линейный член, то есть осуществляют линеаризацию модели в окрестности 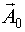 .
.
По МНК находят оценку 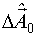 , то есть оценку разности между истинным значением
, то есть оценку разности между истинным значением 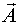 и
и 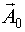 :
: 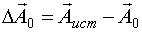 .
.
Находится приближение: 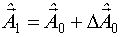 .
.
Далее функция раскладывается в ряд Тейлора в окрестности 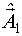 .
.
Находится 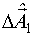 и так далее.
и так далее.
Процедура заканчивается на той операции, на которой норма вектора 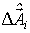 становится меньше некоторой, достаточно малой, величины
становится меньше некоторой, достаточно малой, величины 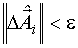 .
.
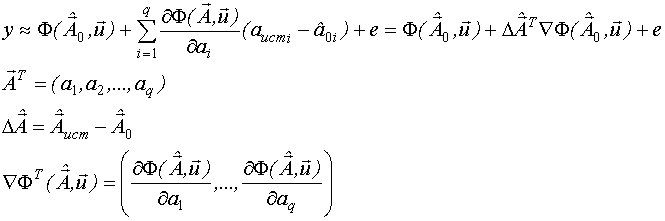
Получена линеаризованная по параметрам модель, в которой неизвестны коэффициенты 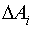 . Оценка
. Оценка 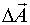 возможна МНК.
возможна МНК.
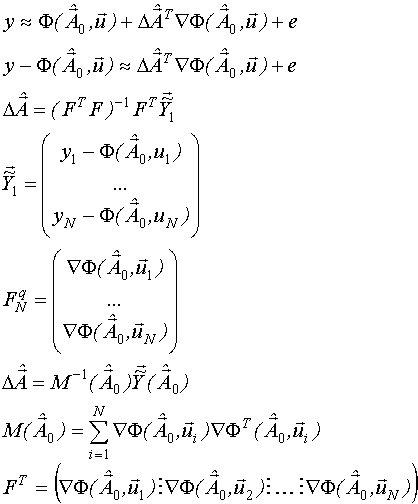
Каждый элемент суммы представляет собой матрицу размером q*q, являющуюся информационной матрицей Фишера для одного измерения входа-выхода.
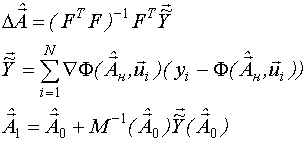
В общем виде алгоритм Гаусса-Ньютона можно записать следующим образом:
Метод Хартли
Процедура Хартли отличается от процедуры Гаусса-Ньютона тем, что используются не все значения 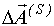 , а только часть его.
, а только часть его.
Метод Марквардта
Метод Марквардта отличается тем, что вместо матрицы М используется матрица 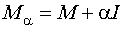 , где I- единичная матрица. Говорят, что матрица
, где I- единичная матрица. Говорят, что матрица 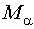 лучше обусловлена (имеет определитель больше, чем у матрицы М).
лучше обусловлена (имеет определитель больше, чем у матрицы М).
По экспериментальным данным
Нелинейных объектов
Модель Винера
Модель Гаммерштейна
Модель Винера-Гаммерштейна
Модель Вольтерра
План эксперимента
10.2.4. Критерии оптимальности планов и моделей
ОСНОВНЫЕ ИДЕИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА.
Пусть имеется объект,
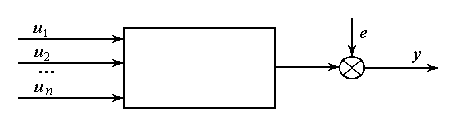
структура модели которого является линейно-параметризованной.

МНК-оценка вектора неизвестных коэфициентов:
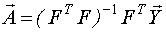
Качество модели характеризуется ковариационной матрицей 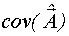 .
.
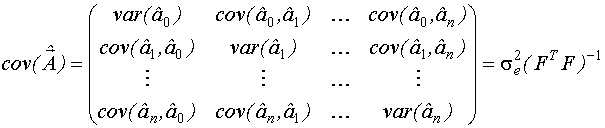
В случае линейной параметризации модели информационная матрица определяется на основе измерений входных переменных объекта (то есть информационная матрица определяется матрицей входных переменных  ) и не зависит от значений выхода, полученных по результатам эксперимента.
) и не зависит от значений выхода, полученных по результатам эксперимента.
В случае линейной параметризации модели имеется возможность так спланировать эксперимент, то есть определить такую матрицу входных переменных, при которой ковариационная матрица оценок неизвестных параметров обладает теми или иными желаемыми свойствами. В пассивном эксперименте, когда матрица входных переменных является во многом случайной, ковариационная матрица оценок чаще всего является плохо обусловленной (то есть ее детерминант близок к нулю), поэтому планирование эксперимента, то есть активное экспериментирование, когда входные переменные не просто измеряются, а устанавливаются на некоторых оптимальных уровнях, позволяет получить модели, обладающие теми или иными оптимальными свойствами.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
ТЕОРИИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА.
Факторы планирования.
Факторами планирования будем называть управляемые входные переменные
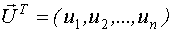
Пространство планирования.
Пространство планирования 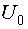 - это область в n-мерном пространстве, внутри и на границах которой можно проводить опыты. Область планирования может быть правильной и произвольной формы.
- это область в n-мерном пространстве, внутри и на границах которой можно проводить опыты. Область планирования может быть правильной и произвольной формы.
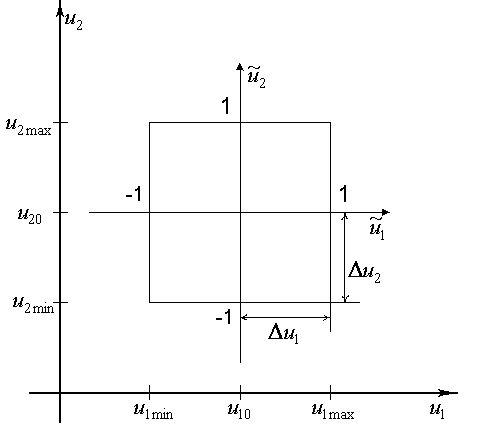
Обычно факторы планирования нормируют следующим образом:
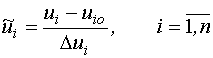
 - координата центра области планирования;
- координата центра области планирования;
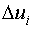 - половина интервала планирования.
- половина интервала планирования.
Нормированное пространство планирования (пространство планирования для нормированных факторов) представляет собой единичный n-мерный гиперкуб.
На этапе планирования эксперимента обычно используются нормированные факторы, а на этапе обработки результатов эксперимента вначале получают модель для нормированных факторов, а затем осуществляют переход к исходным факторам путем замены нормированных факторов их выражениями.
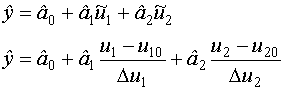
Большинство известных планов предполагают, что областью планирования являются либо единичный n-мерный гиперкуб, либо единичная гиперсфера.
План эксперимента.
План эксперимента ( ) - это совокупность точек пространства планирования, в которых производятся опыты.
План эксперимента задается спектром плана и частотами повторений наблюдений в точках спектра.
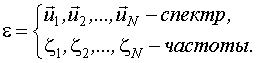
Спектр ("скелет плана") - это совокупность неповторяющихся точек пространства планирования, в которых производятся опыты.
Частота повторения наблюдений в i-ой точке определяется:
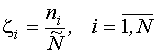 ,
,
где 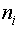 - число опытов в i-ой точке спектра;
- число опытов в i-ой точке спектра;
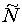 - общее число опытов, предусмотренных планом;
- общее число опытов, предусмотренных планом;

Планы делятся на точные и непрерывные.
План называется точным, если в нем все точно известно, то есть общее число опытов и число опытов в i-ой точке плана известны и являются целымивеличинами.
План называется непрерывным или асимптотическим, если для заданного значения общего числа опытов не все значения числа опытов в i-ой точке являются целыми величинами. Если для данного значения числа опытов план не является точным, то его необходимо округлить до ближайшего точного плана при том же общем числе опытов, либо изменить общее число опытов.
Критерии оптимальности планов и моделей.
Каждый план и полученная на его основе регрессионная модель должны удовлетворять соответствующему критерию оптимальности.
Критерии оптимальности делятся на две группы. К первой группе относятся критерии, характеризующие точность оценок неизвестных параметров модели; ко второй √ критерии, характеризующие предсказательные свойства, полученной на основе плана модели регрессии.
Первая группа:
1) критерий ортогональности,
2) D-оптимальность,
3) A-оптимальность и т.д.
Вторая группа:
1) рототабельность,
2) G-оптимальность,
3) Q-оптимальность и т.д.
Критерий ортогональности.
План называется ортогональным, если соответствующая ему ковариационная матрица оценок параметров модели диагональная:
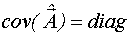
Ортогональный план обеспечивает некоррелированность МНК - оценок неизвестных параметров модели.
D-оптимальность.
План называется D-оптимальным, если он минимизирует определитель ковариационной матрицы оценок, то есть:

Критерий D-оптимальности обеспечивает минимизацию объема эллипсоида рассеивания оценок параметров модели или обобщенную дисперсию оценок.
Пусть имеется модель 

В результате многократного повторения идентификации получим точки, попадающие в область, ограниченную эллипсом рассеивания.
Внутри эллипса находится точка с координатами равными истинным значениям неизвестных параметров модели.
Объем эллипсоида рассеивания прямо пропорционален определителю ковариационной матрицы.
А-оптимальность.
План называется А-оптимальным, если он минимизирует след ковариационной матрицы оценок неизвестных параметров

Этот критерий минимизирует сумму дисперсий оценок неизвестных параметров.
Недостаток данного критерия состоит в том, что он не учитывает коррелированность оценок неизвестных параметров.
Вторую группу критериев оптимальности составляют критерии, обеспечивающие те или иные свойства дисперсионной функции регрессионной модели, то есть функции, определяющей зависимость дисперсии предсказания выхода по модели от координат точки предсказания.
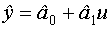
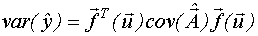 - дисперсионная функция
- дисперсионная функция

Рототабельность.
План называется рототабельным, если дисперсия предсказания выхода по соответствующей ему модели зависит только от расстояния точки предсказания от центра области планирования и не зависит от направления предсказания, то есть в точках равноудаленных от центра области планирования дисперсия предсказания одинакова.
Критерий рототабельности удобен, если получаемая регрессионная модель используется при статической оптимизации параметров или режимов объектов. При этом предполагается, что оптимизация осуществляется поисковыми методами.
G-оптимальность.
План называется G-оптимальным или минимаксным, если он минимизирует максимальную по пространству планирования дисперсию предсказания выхода.


Максимальная дисперсия должна быть минимальна по пространству планирования.
Существует теорема эквивалентности, согласно которой для линейно-параметризованных моделей критерии D- и G-оптимальности эквивалентны. То есть D-оптимальный план является G-оптимальным инаоборот.
Q-оптимальность.
План называется Q-оптимальным, если он минимизирует среднюю по пространству планирования дисперсию предсказания выхода.
Тема 11. Ортогональные планы первого порядка
11.1. Назначение и типы ортогональных планов первого порядка
11.2. Полный факторный эксперимент (ПФЭ, 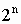 )
)
11.3. Вычисление МНК-оценок и их свойства при ортогональном планировании первого порядка.
Полуреплики
Четвертьреплики
НАЗНАЧЕНИЕ ДРОБНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА
Дробный факторный эксперимент предназначен для построения тех же моделей, что и полный факторный эксперимент:
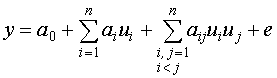
При дробном факторном эксперименте факторы делятся на две группы: основные и вспомогательные (дополнительные). При этом число вспомогательных факторов - , основных - (n-), число опытов - 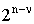 . Если =1, то план называется полурепликой от полного факторного эксперимента, если =2 √ 1/4 репликой, если =3 √ 1/8 репликой и так далее.
. Если =1, то план называется полурепликой от полного факторного эксперимента, если =2 √ 1/4 репликой, если =3 √ 1/8 репликой и так далее.
ПОЛУРЕПЛИКИ
Полуреплика √ это половина полного факторного эксперимента.
Рассмотрим пример при числе факторов n=3
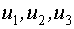
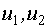 -основные факторы.
-основные факторы.
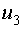 - вспомогательный фактор.
- вспомогательный фактор.
Для построения матрицы дробного факторного эксперимента необходимо задать генерирующие соотношения (ГС), то есть определить, какому произведению основных факторов соответствует дополнительный фактор.
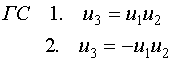
В дробном факторном эксперименте факторы всегда изменяются по плану полного факторного эксперимента типа 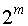 , где m=n-.
, где m=n-.
| u1 | u2 | u3 |
| +1 | +1 | +1 |
| -1 | +1 | -1 |
| +1 | -1 | -1 |
| -1 | -1 | +1 |
Матрица плана дробного факторного эксперимента обладает теми же свойствами, что и матрица полного факторного эксперимента. Матрица базисных функций, соответствующая дробному факторному эксперименту, так же удовлетворяет тем же свойствам, за исключением первого столбца, для которого не выполняется первое свойство.
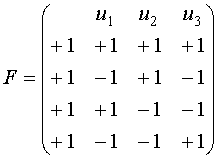
Вычисление оценок неизвестных коэффициентов модели производится по тем же формулам, что и для полного факторного эксперимента: