Системы дифференциальных уравнений
Во многих практических технических и физических задачах требуется определить сразу несколько функций, связанных между собой несколькими дифференциальными уравнениями. Совокупность таких уравнений называется системой дифференциальных уравнений. Обычно число уравнений соответствует числу неизвестных функций. В частности, к таким системам приводят задачи о движении материальных тел в пространстве под действием заданных сил.
Рассмотрим упрощенный вариант такой задачи, связанный с материальной точкой. Пусть 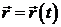 описывает закон движения материальной точки в трехмерном пространстве, где
описывает закон движения материальной точки в трехмерном пространстве, где 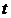 – время. Значит, в каждый момент времени положение точки характеризуется радиус-вектором
– время. Значит, в каждый момент времени положение точки характеризуется радиус-вектором 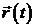 или, что то же самое, тремя его координатами
или, что то же самое, тремя его координатами 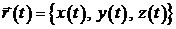 . Если на точку действует сила
. Если на точку действует сила 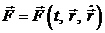 , то можно составить уравнение движения
, то можно составить уравнение движения 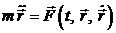 . Но если равны два вектора, то должны быть равны и их соответствующие координаты:
. Но если равны два вектора, то должны быть равны и их соответствующие координаты:
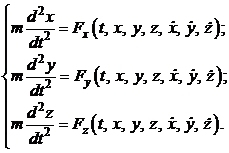
В результате получена система из трех дифференциальных уравнений второго порядка. Так как она описывает движение точки, то данная система называется динамической. Если правые части данной системы явно от времени 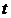 не зависят то такая система называется стационарной или автономной.
не зависят то такая система называется стационарной или автономной.
Обычно системы дифференциальных уравнений высших порядков приводятся к системе первого порядка. Для этого произведем замену 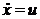 ,
, 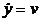 ,
, 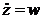 . В результате получим систему из шести дифференциальных уравнений, но уже первого порядка:
. В результате получим систему из шести дифференциальных уравнений, но уже первого порядка:
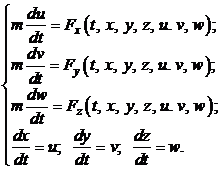
Решение данной системы дает шесть функций 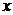 ,
, 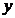 ,
, 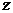 ,
, 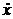 ,
, 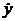 ,
, 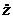 . Их рассматривают как координаты некоторого вектора
. Их рассматривают как координаты некоторого вектора 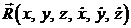 в шестимерном фазовом пространстве. Сам вектор
в шестимерном фазовом пространстве. Сам вектор 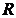 при этом называется фазовой траекторией.
при этом называется фазовой траекторией.
Итак, движение одной материальной точки описывается тремя уравнениями второго порядка или шестью уравнениями первого порядка. При этом следует иметь в виду, что материальная точка имеет три степени свободы. Если взять твердое тело, то оно имеет шесть степеней свободы, и соответственно этому движение тела описывается шестью дифференциальными уравнениями второго порядка или двенадцатью первого. Из этих рассуждений можно сделать вывод, что система с 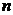 степенями свободы описывается
степенями свободы описывается 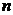 дифференциальными уравнениями второго порядка или
дифференциальными уравнениями второго порядка или 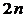 дифференциальными уравнениями первого порядка, то есть одной степени свободы соответствует одно дифференциальное уравнение второго порядка или два – первого.
дифференциальными уравнениями первого порядка, то есть одной степени свободы соответствует одно дифференциальное уравнение второго порядка или два – первого.
В связи со сказанным выше в дальнейшем будем рассматривать только системы дифференциальных уравнений первого порядка следующего вида:
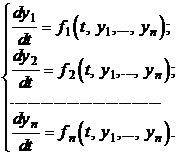
Определение 3.19.1. Система дифференциальных уравнений, левые части которых содержат лишь производные первого порядка одной из искомых функций, а правые части не содержат производных, называется нормальной.
Определение 3.19.2. Решением системы дифференциальных уравнений называется совокупность функций 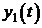 ,
, 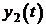 ,…,
,…, 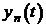 , которые каждое уравнение системы обращают в тождество.
, которые каждое уравнение системы обращают в тождество.
Теорема Коши. Пусть правые части нормальной системы дифференциальных уравнений 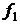 ,
, 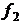 ,…,
,…, 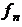 непрерывны вместе со своими частными производными по
непрерывны вместе со своими частными производными по 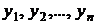 на некотором множестве
на некотором множестве 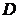 . Тогда каковы бы ни были значения
. Тогда каковы бы ни были значения 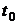 ,
, 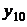 ,
, 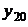 ,…,
,…, 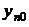 , принадлежащие этому множеству, существует единственное решение системы
, принадлежащие этому множеству, существует единственное решение системы 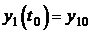 ,
, 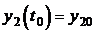 ,…,
,…, 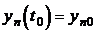 .
.
Вспомним, что общее решение одного дифференциального уравнения первого порядка могло быть представлено в виде однопараметрического семейства кривых, расположенных в одной плоскости. Если взять нормальную систему из двух дифференциальных уравнений
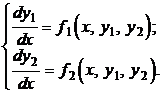
то ее общее решение, ели оно существует, будет иметь вид: 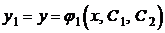 ,
, 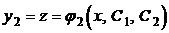 .. Эти решения можно рассматривать как двухпараметрические уравнения пространственной кривой в системе координат
.. Эти решения можно рассматривать как двухпараметрические уравнения пространственной кривой в системе координат 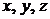 . Следовательно, общее решение одного дифференциального уравнения первого порядка можно изобразить в виде семейства кривых в двумерном пространстве, двух дифференциальных уравнений первого порядка – семейства кривых в трехмерном пространстве. Общее решение
. Следовательно, общее решение одного дифференциального уравнения первого порядка можно изобразить в виде семейства кривых в двумерном пространстве, двух дифференциальных уравнений первого порядка – семейства кривых в трехмерном пространстве. Общее решение 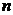 уравнений первого порядка образует семейство кривых, расположенных в пространстве порядка
уравнений первого порядка образует семейство кривых, расположенных в пространстве порядка 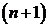 . В этом случае фазовое пространство – это пространство состояний движения точки по интегральной кривой. Очевидно, что для выделения одной траектории должны быть заданы начальные условия, то есть начальное положение точки и ее начальная скорость
. В этом случае фазовое пространство – это пространство состояний движения точки по интегральной кривой. Очевидно, что для выделения одной траектории должны быть заданы начальные условия, то есть начальное положение точки и ее начальная скорость 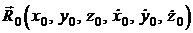 .
.
