Характеристический и минимальный многочлены матрицы.

Для вычисления характеристического многочлена матрицы A используется команда charpoly(A,lambda).

Минимальный многочлен (делитель) матрицы А можно найти с помощью команды minpoly(A,lambda).

Канонические и специальные виды матрицы.

Привести матрицу А к нормальной форме Жордана можно командой jordan(A).

К треугольному виду матрицу А можно привести тремя способами:

1) команда gausselim(A) приводит матрицу А к треугольному виду методом Гаусса;

2) команда ffgausselim(A) приводит матрицу А к треугольному виду методом Гаусса без деления. Эта команда предпочтительней для работы с символьными матрицами, так как не производит нормировку элементов и исключает возможные ошибки, связанные с делением на нуль;

3) команда gaussjord(A) приводит матрицу А к треугольному виду методом Гаусса-Жордана.

Характеристическую матрицу 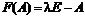можно вычислить командой charmat(A,lambda).

Задание 3.

1. Дана матрица 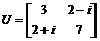. Найти ее собственные векторы и собственные числа.

> U:=matrix([[3,2-I],[2+I,7]]):

> eigenvectors(U);

,

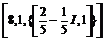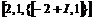
2. Дана матрица 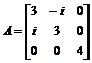. Найти собственные векторы, собственные числа, характеристический многочлен и минимальный многочлен, Жорданову форму.

> A:=matrix([[3,-I,0],[I,3,0],[0,0,4]]):

> eigenvectors(A);

[2, 1, {([1, -I, 0])}], [4, 2, {([0, 0, 1]), ([-I, 1, 0])}]

> P(lambda):=charpoly(A,lambda);

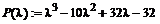
> d(lambda):=minpoly(A,lambda);

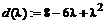
> jordan(A);

3. Дана матрица 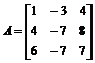. Привести матрицу А к Жордановой форме, треугольному виду, найти ее характеристическую матрицу.

> A:=matrix([[1,-3,4],[4,-7,8],[6,-7,7]]):

> j:=jordan(A);

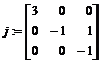
> g:=gausselim(A);

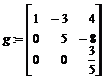
> F:=charmat(A,lambda);

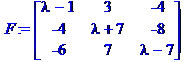
Самостоятельно проверьте, чем будет отличаться результат выполнения команды ffgausselim(A) от gausselim(A) на этом примере.

§4. Системы линейных уравнений. Матричные уравнения

Системы линейных уравнений и матричные уравнения.

Система линейных уравнений 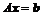может быть решена двумя способами.

Способ 1: стандартная команда solve находит решение системы линейных уравнений, записанных в развернутом виде:

.

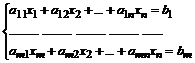Способ 2: команда linsolve(A,b) из пакета linalg находит решение уравнения 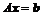. Аргументы этой команды: А – матрица, b – вектор.

С помощью команды linsolve(A,b) можно найти решение матричного уравнения АХ=В, если в качестве аргументов этой команды указать, соответственно, матрицы А и В.

Ядро матрицы.

Ядро матрицы А – это множество векторов х таких, произведение матрицы А на которые равно нулевому вектору: 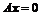. Поиск ядра матрицы А эквивалентен решению системы линейных однородных уравнений. Найти ядро матрицы А можно командой kernel(A).

Задание 4.

1. Найти общее и одно частное решение системы: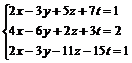

> eq:={2*x-3*y+5*z+7*t=1, 4*x-6*y+2*z+3*t=2,

2*x-3*y-11*z-15*t=1}:

> s:=solve(eq,{x,y,z});

s:={ 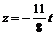, y=y, }

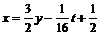Для нахождения частного решения следует выполнить подстановку конкретного значения одной из переменных при помощи команды subs:

> subs({y=1,t=1},s);

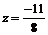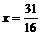{ , , 1=1}

2. Решить матричное уравнение: АX=В; где ,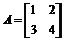

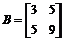
> A:=matrix([[1,2],[3,4]]):

> B:=matrix([[3,5],[5,9]]):

> X:=linsolve(A,B);

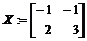
3. Дана матрица 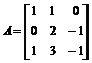. Найти ее ранг, дефект: d(A)=n–r(A), где n – размерность квадратной матрицы, r – ее ранг. Найти ядро А. Наберите:

> A:=matrix([[1,1,0],[0,2,-1],[1,3,-1]]):

> r(A):=rank(A);

r(A):=2

> d(A):=rowdim(A)-r(A);

d(A):=1

> k(A):=kernel(A);

k(A):={[-1,1,2]}

Контрольные задания.

При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:

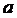- число букв в фамилии студента,

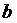- число букв в полном имени студента,

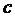- число букв в отчестве студента.

В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, отчество, фамилия).

Задания.

1. Даны векторы 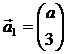, , 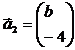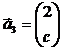. Выполнить следующие задания:

а) найти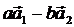

б) найти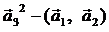

в) найти угол между векторам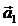и и .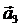

2. Даны матрицы 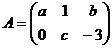, 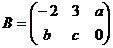Вычислить:

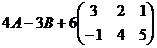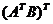a) б) в)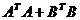

3. Вычислить определители для следующих матриц:

а) 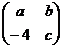б)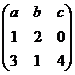

4. Найти обратные для следующих матриц:

a) 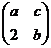б)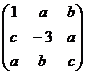

5. Дана матрица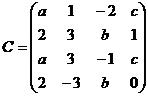

a) Привести матрицу С к треугольному виду.

б) Вычислить M₂₃

в) Найти ранг матрицы.

6. Найти собственные значения и собственные векторы матрицы A=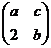

7.Решить матричные уравнения:

а) 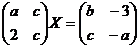б)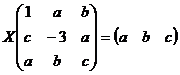

Контрольные вопросы.

1. Какой пакет следует загрузить перед решением задач линейной алгебры в Maple?

2. С помощью каких команд можно ввести вектор, матрицу?

3. Какими двумя командами можно сложить два вектора одинаковой размерности (2 матрицы)?

4. Какие виды произведений векторов вычисляются Maple и какие команды для этого используются?

5. Как вычислить норму вектора?

6. Как вычислить угол между двумя векторами?

7. Опишите команды нахождения базиса системы векторов и построение ортогонального базиса системы векторов.

8. Какими двумя командами можно вычислить произведение двух матриц (или матрицы на вектор)?

9. Какие команды используются для нахождения определителя, минора, алгебраического дополнения, следа матрицы?

10. Что такое дефект матрицы? Опишите способ нахождения дефекта квадратной матрицы. Какие команды при этом используются?

11. Какая матрица называется обратной и какими способами она вычисляется в Maple?

12. Что называется собственным вектором и собственным числом матрицы? Что называется спектром матрицы? Какие команды используются для нахождения спектра матрицы и ее собственных векторов? В каком виде в Maple выводятся результаты выполнения этих команд?

13. Перечислите специальные виды матриц и команды, приводящие матрицы к этим формам.

14. Что называется ядром матрицы, и какая команда используется для его нахождения?

15. Какая команда позволяет решать матричные уравнения?