Институт имени М.Е.Евсевьева»
Институт имени М.Е.Евсевьева»
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ЧИСЛЕННЫЕ МЕТОДЫ
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
К ЛАБОРАТОРНЫМ РАБОТАМ
Саранск 2010
Рецензенты:  Рыбина Т.М., кандидат педагогических наук, доцент кафедры математики МГПИ им. М.Е.Евсевьева;
Рыбина Т.М., кандидат педагогических наук, доцент кафедры математики МГПИ им. М.Е.Евсевьева;
Куплинов В.Н.,кандидат технических наук, доцент кафедры физики МГПИ им. М.Е.Евсевьева.
Рекомендовано для использования УМК физико-математического факультета МГПИ им.М.Е.Евсевьева.
Протокол № 8 от 18.03.2009 года
Составитель: Кормилицына Т.В. – кандидат физико-математических наук, доцент кафедры информатики и ВТ МГПИ им. М.Е.Евсевьева.
Численные методы:методические рекомендации к лабораторным работам / Составитель: Т.В. Кормилицына / Мордов. гос.пед.ин-т. – Саранск, 2009. – 40 с.
Методические рекомендации предназначены для проведения лабораторного практикума по дисциплине «Численные методы» для студентов физико-математического факультета. В тексте содержится теоретический материал, необходимый для выполнения каждой лабораторный работы, алгоритмы решения в табличном процессоре Excel и программы на языке TMTPascal, которые каждый студент может легко адаптировать для выполнения индивидуального задания. Приведены образцы решения наиболее важных задач численного анализа.
Практическая часть содержит задания для самостоятельной работы. Приведены вопросы для подготовки к защите лабораторных работ.
© ГОУ ВПО «Мордовский государственный педагогический институт
им. М.Е. Евсевьева», 2009
© Кормилицына Т.В., 2010
СОДЕРЖАНИЕ
| Лабораторная работа № 1. Теория погрешностей и машинная арифметика………………………………………………………………............................. | |
| Лабораторная работа № 2.Методы решения нелинейных уравнений………………………………………………………………………………... | |
| Лабораторная работа № 3.Методы решения систем линейных уравнений……………………………….………………………………………….……. | |
| Лабораторная работа № 4.Приближение функций. Численное дифференцирование……………………………………….……………………….............. | |
| Лабораторная работа № 5.Численное интегрирование……….………........ | |
| Лабораторная работа № 6.Численное решение задачи Коши………..……. | |
| Список литературы.............................................................................................. |
ЛАБОРАТОРНАЯ РАБОТА № 1
Теория погрешностей и машинная арифметика
Теоретическая часть
Пусть х – некоторое число, число а называется его приближенным значением, если а в определенном смысле мало отличается от х и заменяет х в вычислениях, 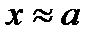 .
.
Погрешностью 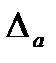 приближенного значения а числа х называется разность
приближенного значения а числа х называется разность 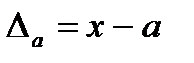 , а модуль этой погрешностью называется абсолютной погрешностью.
, а модуль этой погрешностью называется абсолютной погрешностью.
Если 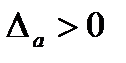 , то а взято с недостатком. Если
, то а взято с недостатком. Если 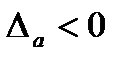 , то а взято с избытком.
, то а взято с избытком.
Границей погрешности приближенного значения а числа х называется всякое неотрицательное число 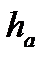 , которое не меньше модуля погрешности:
, которое не меньше модуля погрешности: 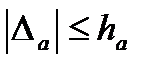 .
.
Говорят, что приближение а приближает число х с точностью до 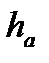 , если
, если 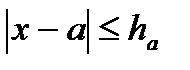 ,
, 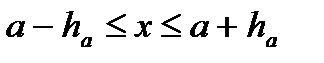 ,
, 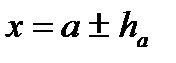 .
.
Пример.Пусть а=0,273 – приближенное значение х с точность до 0,001. Указать границы, в которых заключается х.
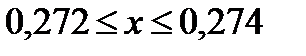
При округлении чисел считают, что границы погрешности округления равна половине единицы округляемого разряда:
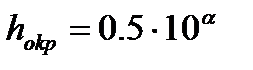 , α – порядок округления разряда.
, α – порядок округления разряда.
Относительной погрешностью приближенного значения а числа х называется отношение
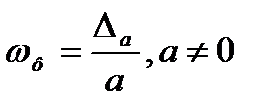 .
.
Пример.Округлить до десятых число 27,52 и найти погрешность и относительную погрешность округления:
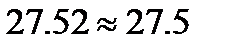 ,
,
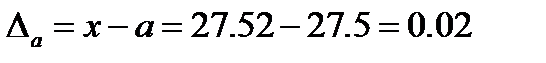 ,
,
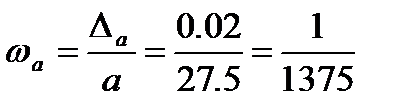 .
.
Также как и абсолютная погрешность, относительная погрешность не всегда может быть вычислена и приходится оценивать ее модуль. Модуль относительной погрешности выражается в процентах. Чем меньше модуль относительной погрешности, тем выше качество приближения.
Пусть 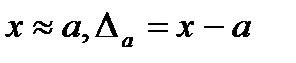 .
.
Цифра приближенного значения а называется верной, если модуль его погрешности не превосходит половины единицы этого разряда.
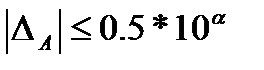 .
.
Очевидно, что все цифры, стоящие слева от верной цифры – верные.
Пример. Пусть х=27,421, а=27,381, 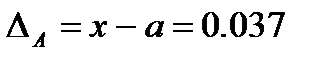 .
.
Выясним, какие цифры верные в приближении а?
4 – 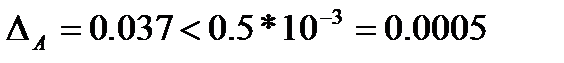 , следовательно, 4 – неверная;
, следовательно, 4 – неверная;
8 – 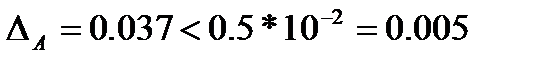 , следовательно, 8 – неверная;
, следовательно, 8 – неверная;
3 – 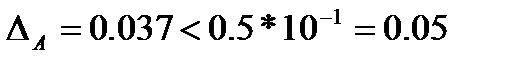 , следовательно, 3 – верная.
, следовательно, 3 – верная.
3,2,7 – верные цифры.
Пример. Если известно, что относительная погрешность приближения 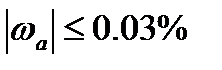 , то это приближение имеет ровно 3 верные значащие цифры.
, то это приближение имеет ровно 3 верные значащие цифры.
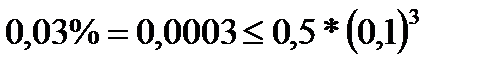 , следовательно, приближение имеет не менее 3-х верных значащих цифр.
, следовательно, приближение имеет не менее 3-х верных значащих цифр.
Практическая часть
Задание 1.Дана функция 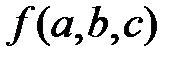 . Значения переменных указаны в варианте со всеми верными цифрами. Оценить погрешность результата, используя: a) оценки погрешностей для арифметических операций; b) общую формулу погрешностей.
. Значения переменных указаны в варианте со всеми верными цифрами. Оценить погрешность результата, используя: a) оценки погрешностей для арифметических операций; b) общую формулу погрешностей.
Результат представить в двух формах записи: с явным указанием погрешностей и с учетом верных цифр.
| № | 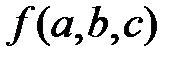 | 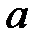 | 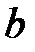 | 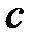 | № | 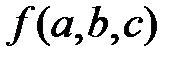 | 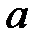 | 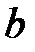 | 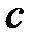 |
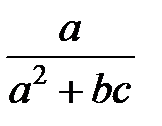 | 0.0125 | 0.283 | 0.0187 | 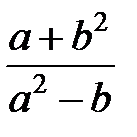 | 4.41 | 18.5 | |||
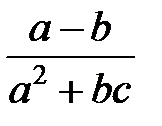 | 14.29 | 13.81 | 10.98 | 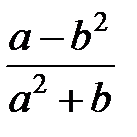 | 16.5 | 4.2 | |||
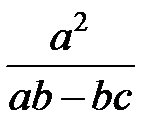 | 12.28 | 13.21 | 12.19 | 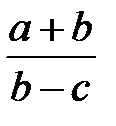 | 52.31 | 48.95 | 47.81 | ||
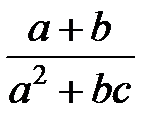 | 0.328 | 0.781 | 0.0129 | 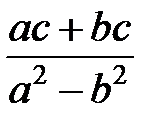 | 4.81 | 4.52 | 9.28 | ||
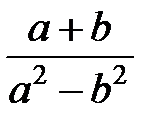 | 14.85 | 15.49 | 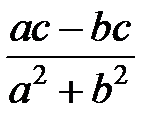 | 16.21 | 16.18 | 21.23 | |||
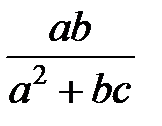 | 12.31 | 0.0352 | 10.82 | 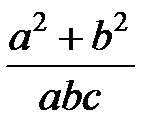 | 0.324 | 1.25 | |||
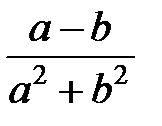 | 12.45 | 11.98 | 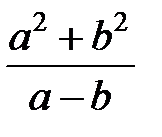 | 25.18 | 24.98 | ||||
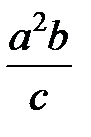 | 3.456 | 0.642 | 7.12 | 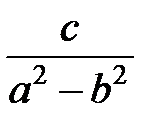 | 3.1415 | 3.1411 | 10.91 | ||
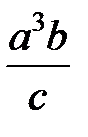 | 1.245 | 0.121 | 2.34 | 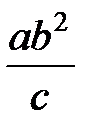 | 3.14 | 1.57 | 0.0921 | ||
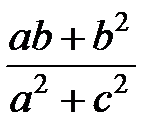 | 13.12 | 0.145 | 15.18 | 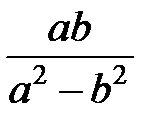 | 14.85 | 15.49 | |||
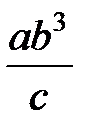 | 0.643 | 2.17 | 5.843 | 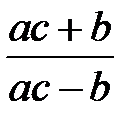 | 5.325 | 5.152 | 5.481 | ||
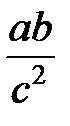 | 0.3575 | 2.63 | 0.854 | 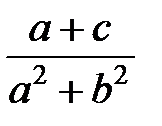 | 71.4 | 4.82 | 49.5 | ||
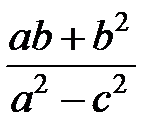 | 14.91 | 0.485 | 14.18 | 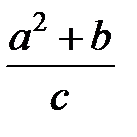 | 4.356 | 4.32 | 0.246 | ||
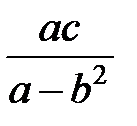 | 16.5 | 4.12 | 0.198 | 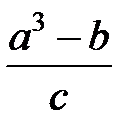 | 3.42 | 5.124 | 0.221 | ||
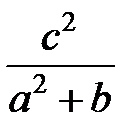 | 5.21 | 14.9 | 0.295 | 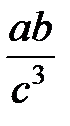 | 0.5761 | 3.622 | 0.0685 |
Задание 2.Вычислить значение 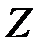 и оценить абсолютную и относительную погрешности результата, считая, что значения исходных данных получены в результате округления.
и оценить абсолютную и относительную погрешности результата, считая, что значения исходных данных получены в результате округления.
Записать результат с учетом погрешности.
| № | 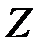 | № | 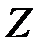 |
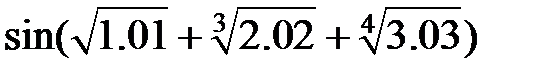 | 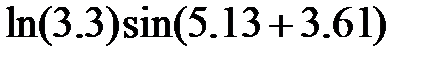 | ||
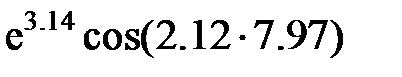 | 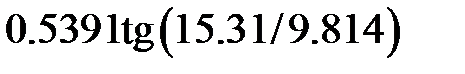 | ||
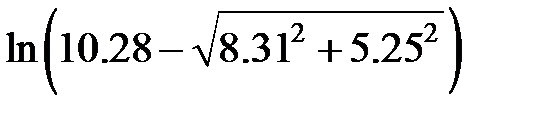 | 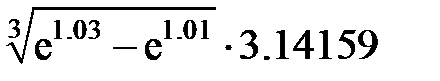 | ||
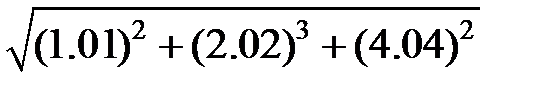 | 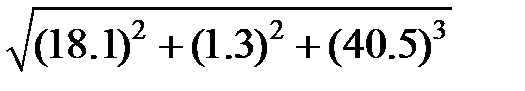 | ||
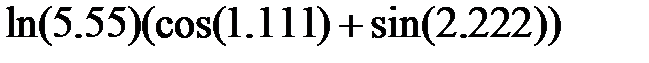 | 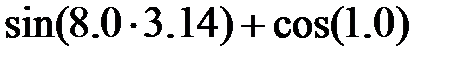 | ||
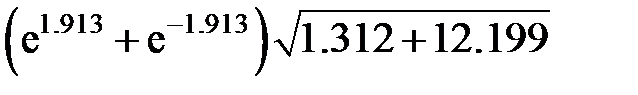 | 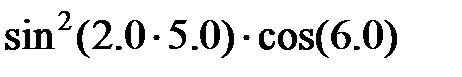 | ||
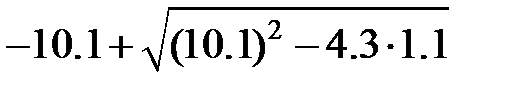 | 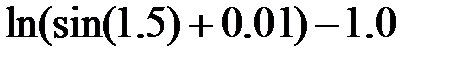 | ||
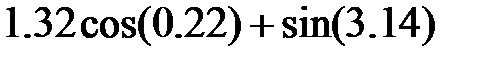 | 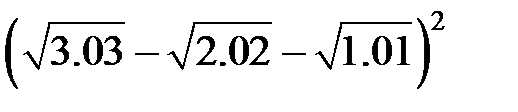 | ||
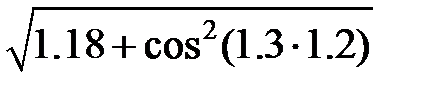 | 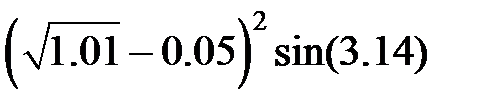 | ||
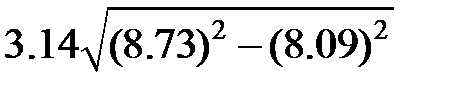 | 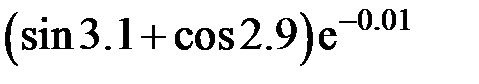 | ||
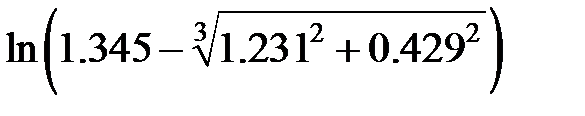 | 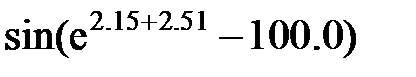 | ||
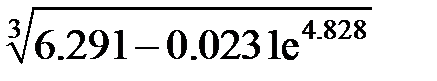 | 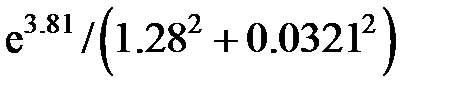 | ||
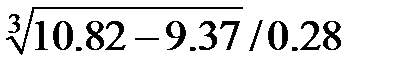 | 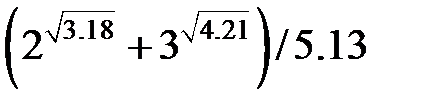 | ||
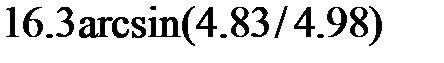 | 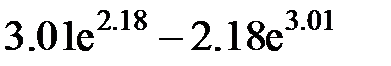 | ||
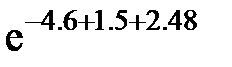 | 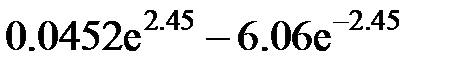 |
Вопросы к защите лабораторной работы №1
«Теория погрешностей и машинная арифметика»
1. Источники и классификация погрешностей. Приближенные числа. Абсолютная и относительная погрешности. Верные и значащие цифры. Способы округления.
2. Погрешности арифметических операций над приближенными числами.
3. Погрешность вычисления функций одной и нескольких переменных.
ЛАБОРАТОРНАЯ РАБОТА № 2
Теоретическая часть
Метод половинного деления (дихотомии или бисекции). Самым простейшим из методов уточнения корней является метод половинного деления, или метод дихотомии, предназначенный для нахождения корней уравнений, представленных в виде f(x)=0.
Пусть непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е.f(a) f(b)<0,тогда на отрезке имеется хотя бы один корень.
Возьмем середину отрезка с=(a+b)/2 (1). Если f(a)∙f(с)<0 (2),то корень явно принадлежит отрезку от a до (a+b)/2 и в противном случае от (a+b)/2 до b. Поэтому берем подходящий из этих отрезков, вычисляем значение функции в его середине и т.д. до тех пор, пока длина очередного отрезка не окажется меньше заданной предельной абсолютной погрешности (b-a)<ε.
Метод простой итерации. В данном методе уравнение f(x)=0 заменяется равносильным уравнением x=φ(x) и строится последовательность значений
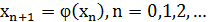 (3).
(3).
Если функция φ(x) определена и дифференцируема на некотором интервале[a, b] и 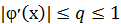 на [a, b], то итерационный процесс xn= φ(xn-1) сходится к корню исходного уравнения x , также содержащегося в интервале [a, b]. Тогда справедливы формулы:
на [a, b], то итерационный процесс xn= φ(xn-1) сходится к корню исходного уравнения x , также содержащегося в интервале [a, b]. Тогда справедливы формулы:
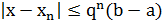 ;
; 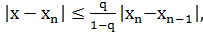 и если требуется найти корень с точностью ε, то кончаем итерационный процесс тогда, когда
и если требуется найти корень с точностью ε, то кончаем итерационный процесс тогда, когда

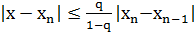 <ε (4).
<ε (4).
Уточнение корней методом касательных (Ньютона). Пусть корень ξ уравнения f(x)=0 отделен на отрезке [a, b], причем первая и вторая производные f'(x) и f''(x) непрерывны и сохраняют определенные знаки при  . Найдя какое-нибудь n-ое приближение корня
. Найдя какое-нибудь n-ое приближение корня 
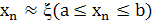
мы можем уточнить его по методу Ньютона следующим образом.
Пусть ξ=xn+hn, где hn - величина малая. Отсюда по формуле Тейлора получим: f(xn + hn) ≈ f(xn)+hn f '(xn)=0. Следовательно, 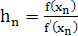 .Подставив полученное выражение в формулу ξ=xn+hn, найдем следующее значение корня:
.Подставив полученное выражение в формулу ξ=xn+hn, найдем следующее значение корня:
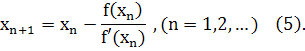
Рекомендуется в качестве начального приближения х0 выбирать такую точку, где f(x0)f''(x0)>0.
Точность вычисления определяется по формуле: 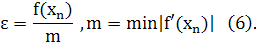
Метод хорд.Пусть дано уравнение f(x)=0, где функция f(x) определена и непрерывна на интервале [a, b] и f(a)f(b)<0. Пусть для определенности f(a)<0 и f(b)>0. Разделим отрезок [a, b] в отношении - f(a):f(b). Это даст нам приближенное значение корня x1 = a + h1, где 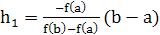 . Далее этот прием применяем к одному из отрезков [a, x1] или [x1, b], на концах которого функция f(x) имеет противоположные знаки. Аналогично находим второе приближение x2 и т.д.
. Далее этот прием применяем к одному из отрезков [a, x1] или [x1, b], на концах которого функция f(x) имеет противоположные знаки. Аналогично находим второе приближение x2 и т.д.
Полагая, что на отрезке [a, b] вторая производная f''(x) сохраняет постоянный знак, метод хорд сводится к двум различным вариантам:
1) x0=b, 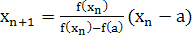 . (7)
. (7)
2) x0=a, 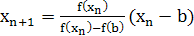 . (8)
. (8)
Таким образом, для вычисления корня уравнения имеем две различные вычислительные формулы. За неподвижный конец выбираем тот конец, для которого знак функции f(x) совпадает со знаком второй производной f''(x). Точность вычисления определяется по формуле (6).
Практическая часть
План решения нелинейного уравнения
Отделить корни, выбрать один отрезок длинной 1 или менее.
1. Представить уравнение в виде f(x)=0, найти отрезок (а : б).
2. Выбрать метод уточнения, обосновать выбор (f’, f” в точках (а : б); определить неподвижную точку метода хорд и точку касания).
3. Составить расчетную формулу метода.
4. Выполнить расчеты по формуле; построить графики.
5. Ответ (последовательность приближенных решений с округленным последним значением).
Задание 1. Отделить корни и уточнить методом хорд, методом секущих, методом итераций с точностью 0,001.
| N | f(x) | N | f(x) |
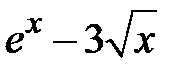 | 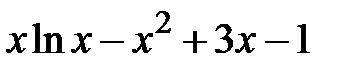 | ||
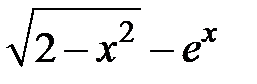 | 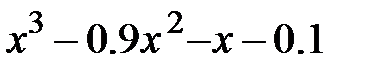 | ||
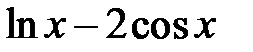 | 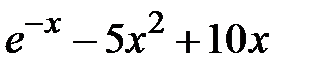 | ||
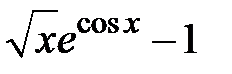 | 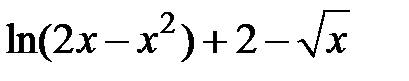 | ||
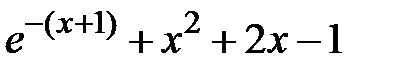 | 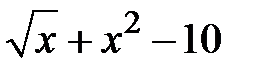 |
Задание 2. Уточнить корень уравнений g(x)=0, отделенный на указанном отрезке, комбинированным методом
| № варианта | g(x) | [a, b] |
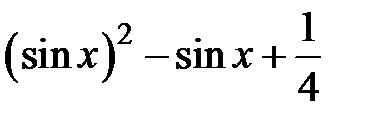 | 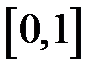 | |
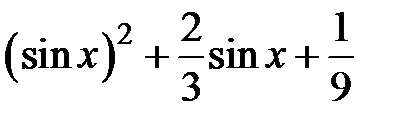 | 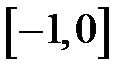 | |
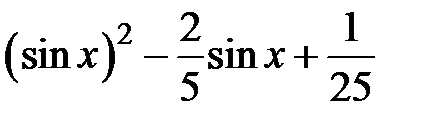 | 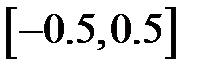 | |
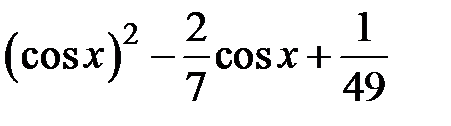 | 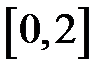 | |
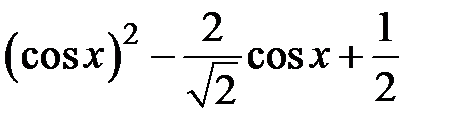 | 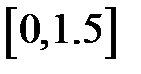 | |
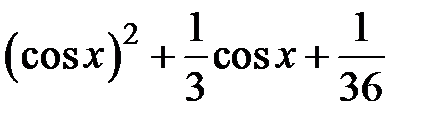 | 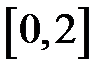 | |
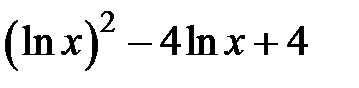 | [5,25] | |
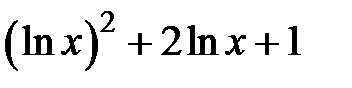 | [0.1,10] | |
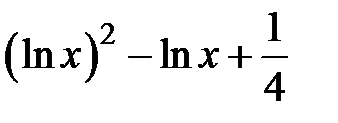 | [0.1,2] | |
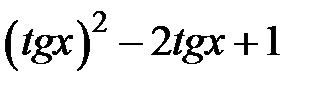 | 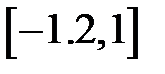 | |
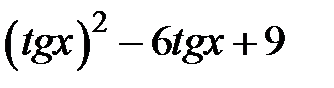 | 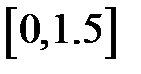 | |
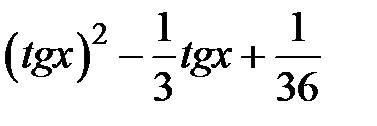 | 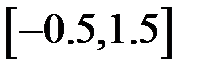 | |
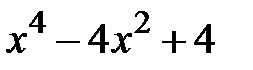 | [0,3] | |
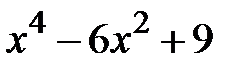 | [0,2] | |
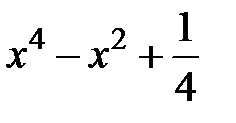 | [0,3] | |
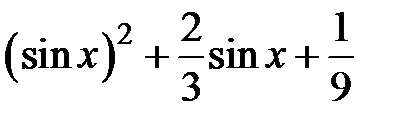 | 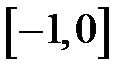 | |
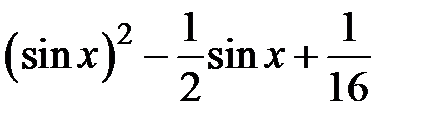 | 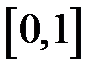 | |
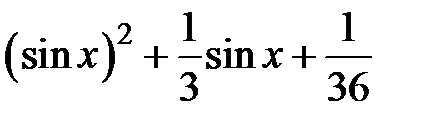 | 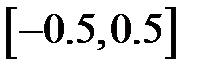 | |
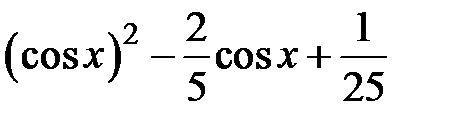 | 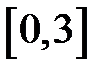 | |
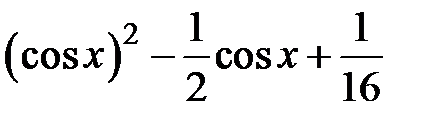 | 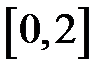 | |
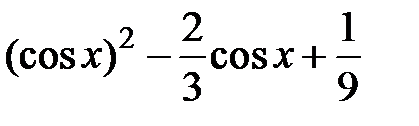 | 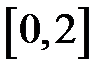 | |
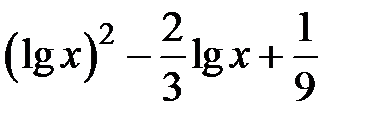 | [0.001,3] | |
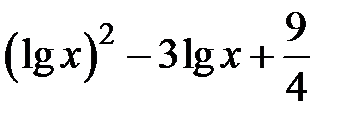 | [0.1,35] | |
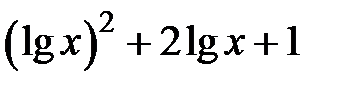 | [0.01,3] | |
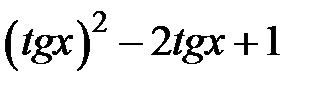 | 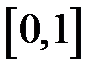 | |
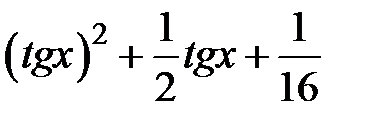 | [-0.5,1.5] | |
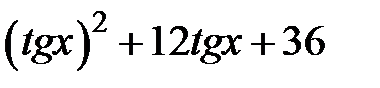 | [-1.5,0] | |
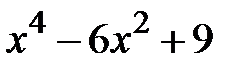 | [1,3] | |
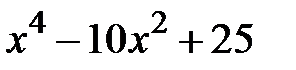 | [0,3] | |
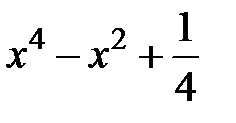 | [0,5] |
Вопросы к защите лабораторной работы №2
«Решение нелинейных уравнений».
1. Постановка задачи решения нелинейных уравнений. Основные этапы решения задачи.
2. Итерационное уточнение корней: порядок сходимости метода.
3. Метод бисекции: описание метода, скорость сходимости, критерий окончания.
4. Метод простой итерации решения нелинейного уравнения: описание метода, условие и скорость сходимости, критерий окончания, геометрическая иллюстрация, приведение к виду, удобному для итераций.
5. Метод Ньютона решения нелинейного уравнения: описание метода, теорема о сходимости, критерий окончания, геометрическая иллюстрация.
6. Метод секущих: описание метода, теорема о сходимости, критерий окончания, геометрическая иллюстрация.
ЛАБОРАТОРНАЯ РАБОТА №3
Теоретическая часть
Метод Гаусса. Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Вычисления с помощью этого метода заключаются в последовательном исключении неизвестных из системы, для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
Схема полного деления.
Задача. Решить систему уравнений по схеме полного деления:
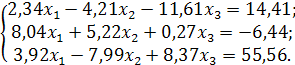
Решение:
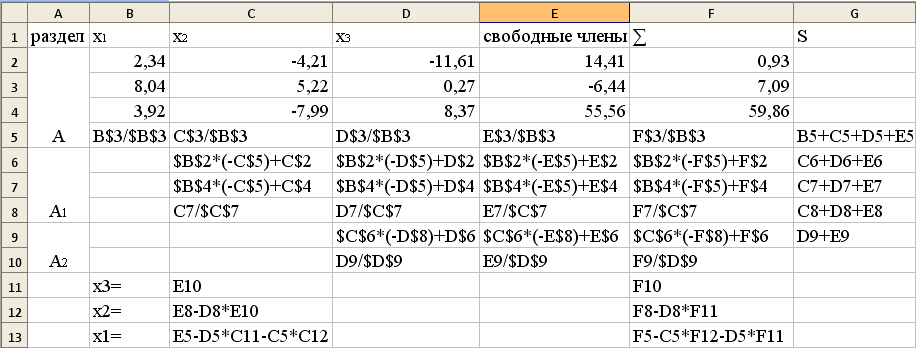
Результат:
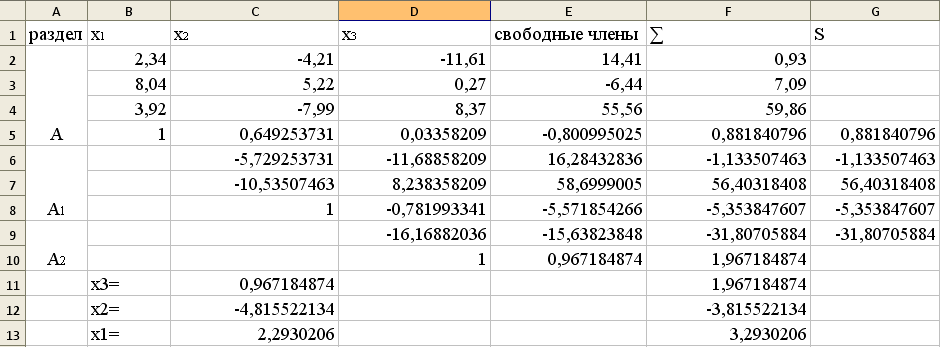
Решение системы: x1=2,2930206,x2=-4,815522134,x3=0,967184874.
Методом Зейделя
Задача. Решить систему уравнений методом Зейделя:
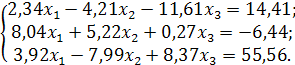
Решение. Воспользуемся формулами (11), (12) и (13):
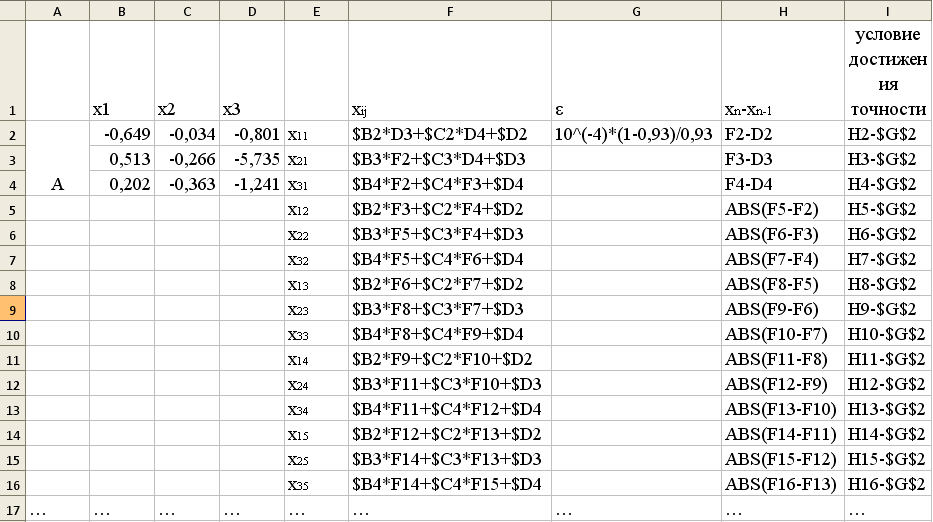
Результат:
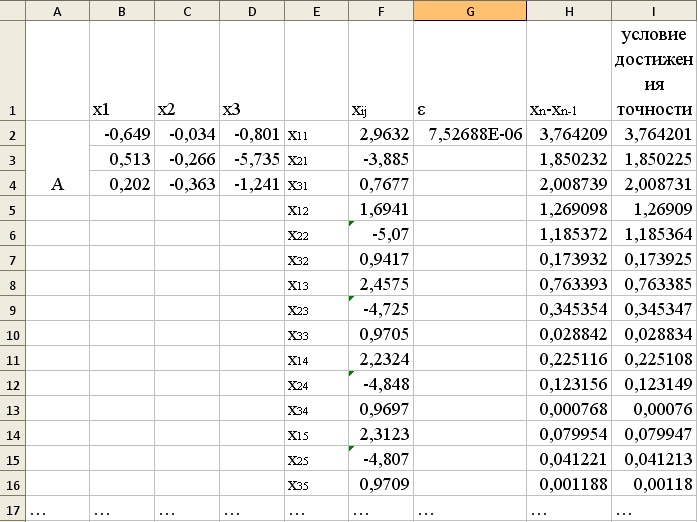
Решение системы: x1≈2,232388,x2≈-4,84794,x3≈0,969745.
Решение достигается более чем за 14 итераций, т.е. трудоемко и занимает много времени.
Задача. Решить методом итераций СЛАУ, оценив предварительно гарантированное количество итераций. Точность 0,001
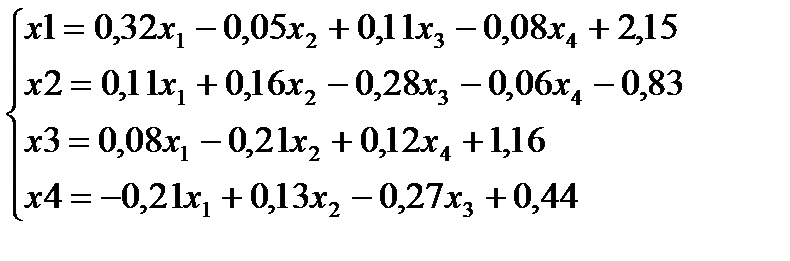
Решение.
Для применения метода итераций с заданной точностью ε применим оценку
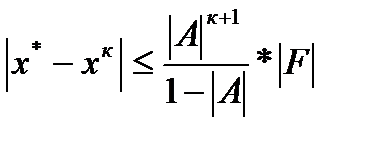 ,
,
где А константа из формул критерия сходимости итерационного процесса
F-мах[|b1|,|b2|,|b3|]
Рассчитаем А по формуле |А|3= 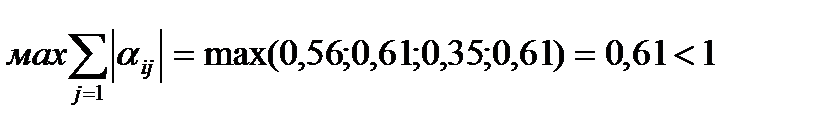

Значит, система имеет итерационный вид, т.е. можно построить последовательность решений по правой части исходной системы.
Если модуль |А|>1, то следует проверить формулу 4,5
Если формулы 3-5 не выполняются система не имеет итерационный вид, значит, метод итераций не применим, следует преобразовать исходную систему.
Вычислим |F|
|F|={2,15;0,83,1,16;0,44}=2,15=b1
Рассчитаем значение k (число итераций) с учётом точности ε=0,001
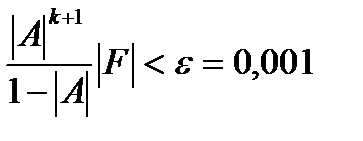
Заменим переменные их значениями
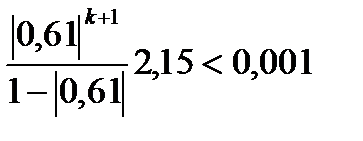 решим неравенство логарифмированием неравенства
решим неравенство логарифмированием неравенства
lg(0,61k+1)-lg(0,39)+lg(2,15)<lg10-3
(k+1)*lg(0,61)<lg(0,39)+3-lg(2,15)
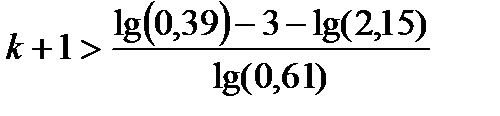
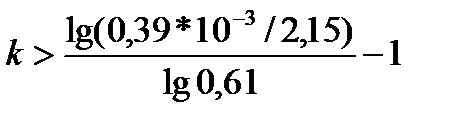
k=k-1 k>17,5-1, к>17
Вывод: для достижения заданной точности требуется выполнять по максимуму 17 итераций, на практике сходимость достигается раньше.
Алгоритм решения системы линейных уравнений в TMTPascal:
1) Метод итераций. Предварительно система должна быть приведена к итерационному виду.
program Iter_sys;
const
a11=0.24; a12=0.21; a13=0.06; a14=-0.34;
a21=0.05; a22=0; a23=0.32; a24=0.12;
a31=0.35; a32=-0.27; a33=0; a34=-0.05;
a41=0.12; a42=-0.43; a43=0.34; a44=-0.21;
b1=1.42; b2=-0.57; b3=0.68; b4=-2.14;
var
x1,x2,x3,x4:real;
xx1,xx2,xx3,xx4:real;
i:integer;
begin
x1:=b1; x2:=b2; x3:=b3; x4:=b4;
for i:=1 to 104 do
begin
xx1:=a11*x1+a12*x2+a13*x3+a14*x4+b1;
xx2:=a21*x1+a22*x2+a23*x3+a24*x4+b2;
xx3:=a31*x1+a32*x2+a33*x3+a34*x4+b3;
xx4:=a41*x1+a42*x2+a43*x3+a44*x4+b4;
writeln(xx1:6:3, xx2:6:3, xx3:6:3, xx4:6:3);
x1:=xx1;
x2:=xx2;
x3:=XX3;
X4:=XX4;
END;
READLN;
END.
Результат:

2)Метод Зейделя. Предварительно система должна быть приведена к специальному виду:
program Zeydel_sys;
const
a11=0; a12=-0.949; a13=-0.511;
a21=-1.034; a22=0; a23=0.417;
a31=-0.533; a32=0.399; a33=0;
b1=0.2173; b2=-1.252; b3=-1.705;
var
x1,x2,x3:real;
xx1,xx2,xx3:real;
i:integer;
begin
x1:=b1; x2:=b2; x3:=b3;
for i:=1 to 30 do
begin
xx1:=-a12*x2-a13*x3+b1;
x1:=xx1;
xx2:=-a21*x1-a23*x3+b2;
x2:=xx2;
xx3:=-a31*x1-a32*x2+b3;
x3:=XX3;
writeln(xx1:6:3, xx2:6:3, xx3:6:3);
END;
READLN;
END.
Результат:
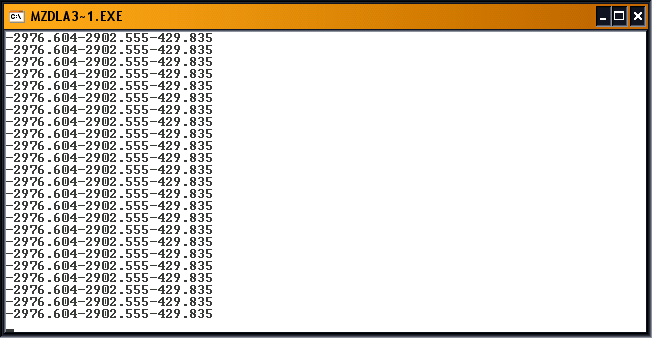
Практическая часть
Задание 1.Решить систему методом Гаусса, предварительно исследовать совместность.
Вариант 1 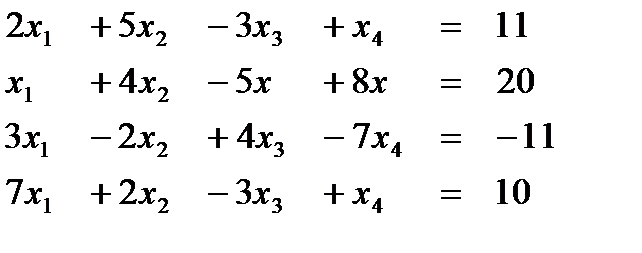 Ответ (1; 2; 1; 2) Ответ (1; 2; 1; 2) | Вариант 2 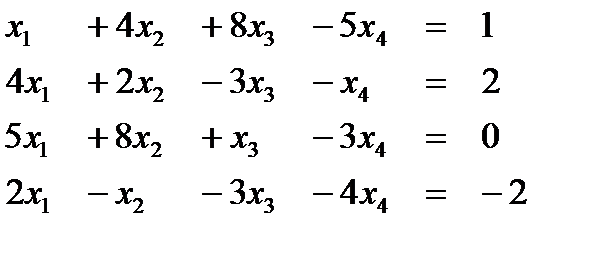 Ответ (2; -1; 1; 1) Ответ (2; -1; 1; 1) |
Вариант 3 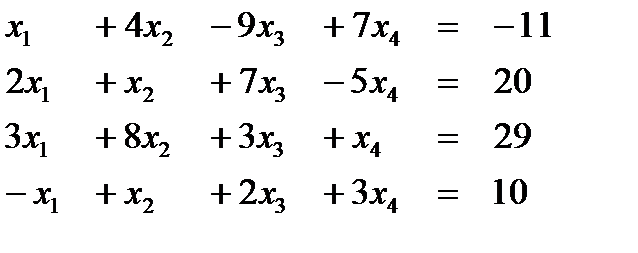 Ответ (1; 2; 3; 1) Ответ (1; 2; 3; 1) | Вариант 4 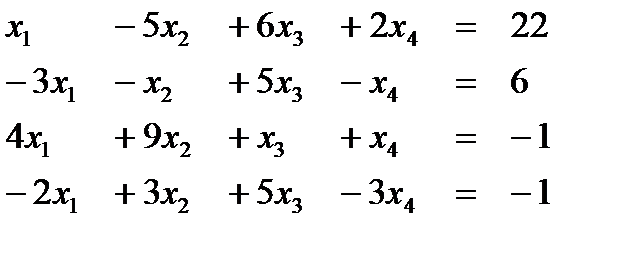 Ответ (1; -1; 2; 2) Ответ (1; -1; 2; 2) |
Вариант 5 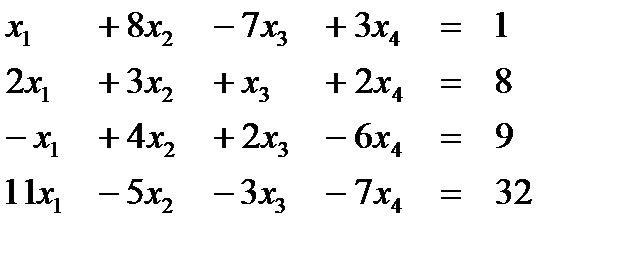 Ответ (3; 1; 1; -1) Ответ (3; 1; 1; -1) | Вариант 6 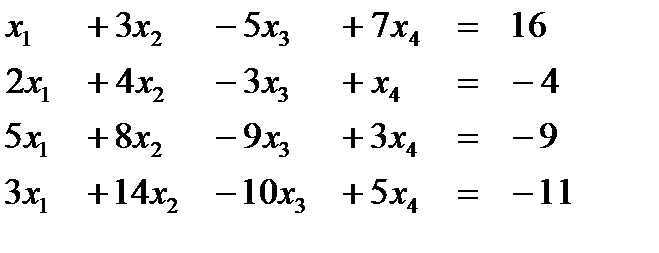 Ответ (1; -1; 2; 4) Ответ (1; -1; 2; 4) |
Вариант 7 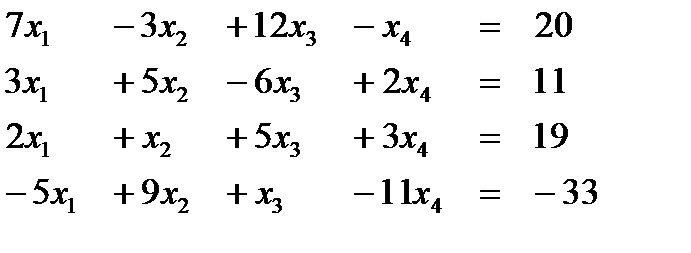 Ответ (2; 1; 1; 3) Ответ (2; 1; 1; 3) | Вариант 8 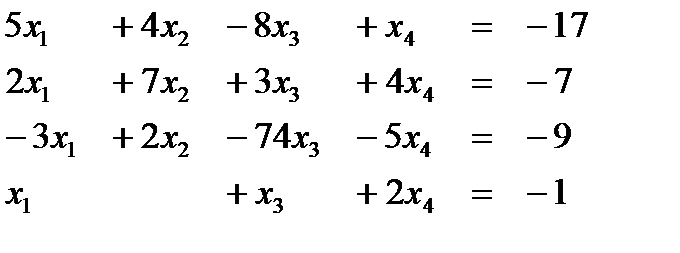 Ответ (1; -1; 2; -2) Ответ (1; -1; 2; -2) |
Вариант 9 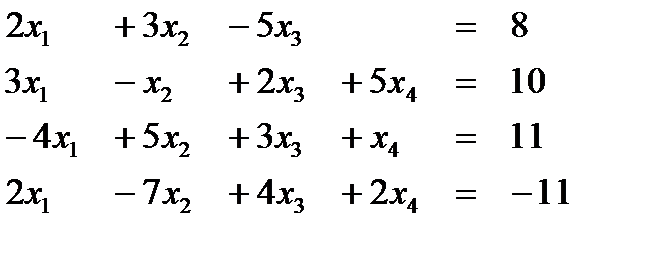 Ответ (2; 3; 1; 1) Ответ (2; 3; 1; 1) | Вариант 10 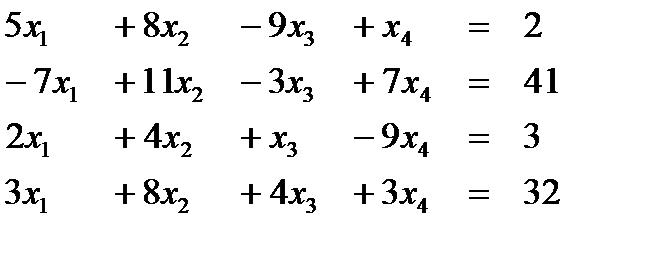 Ответ (-1; 3; 2; 1) Ответ (-1; 3; 2; 1) |
Вариант 11 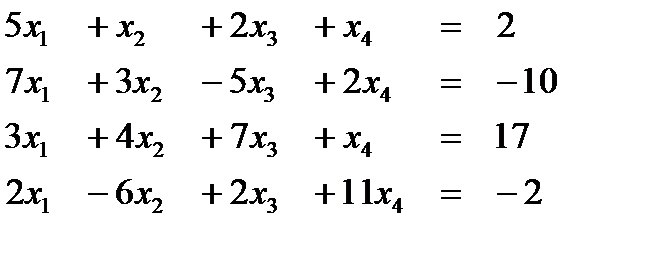 Ответ (-1; 1; 2; 2) Ответ (-1; 1; 2; 2) | Вариант 12 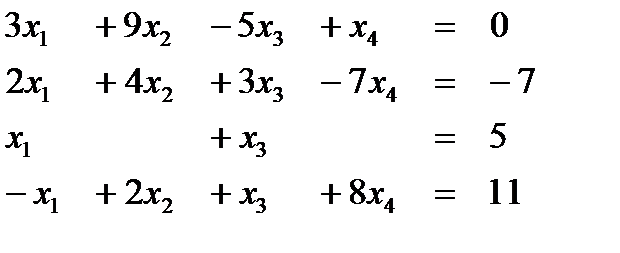 Ответ (4; -1; 1; 2) Ответ (4; -1; 1; 2) |
Вариант 13 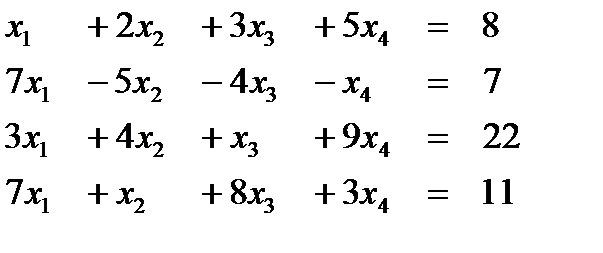 Ответ (2; 2; -1; 1) Ответ (2; 2; -1; 1) | Вариант 14 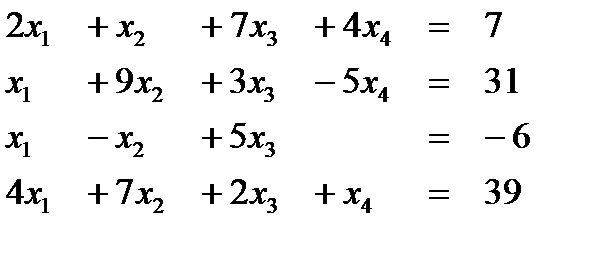 Ответ (3; 4; -1; 1) Ответ (3; 4; -1; 1) |
Вариант 15 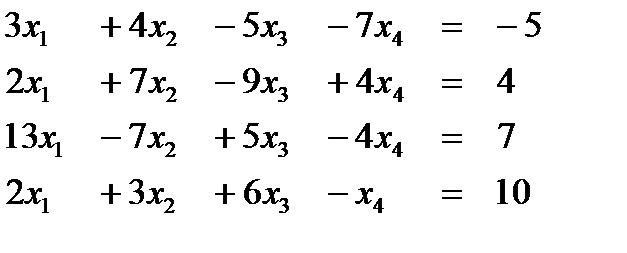 Ответ (1; 1; 1; 1) Ответ (1; 1; 1; 1) | Вариант 16 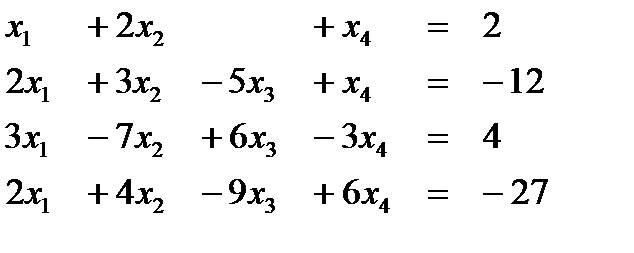 Ответ (-1; 2; 3; -1) Ответ (-1; 2; 3; -1) |
Задание 2. Решить систему из задания 1 методом Зейделя, предварительно приведя ее к специальному виду.
Вопросы к защите лабораторной работы №3
«Решение систем линейных алгебраических уравнений»
1. Метод Гаусса (схема единственного деления): описание метода, трудоемкость метода.
2. Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора): описание метода, его вычислительная устойчивость.
3. Метод простой итерации (Якоби) для решения систем линейных алгебраических уравнений. Сходимость, оценки погрешности, критерий окончания итераций.
4. Метод Зейделя для решения систем линейных алгебраических уравнений. Сходимость, оценки погрешности, критерий окончания итераций. Геометрическая иллюстрация. Алгоритм приведения к виду, обеспечивающему сходимость итерационного процесса.
5. Как привести систему к виду, удобному для итераций по методу простой итерации и определить число итераций, требуемых для достижения точности 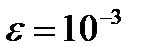 .
.
ЛАБОРАТОРНАЯ РАБОТА № 4
Теоретическая часть
Интерполяционный многочлен Лагранжа.Пусть на отрезке [a,b] некоторая функцияf(x) задана лишь в некоторых точках  , т.е. известны ее значения
, т.е. известны ее значения 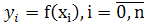 , которые собирают в таблицу:
, которые собирают в таблицу:
| x | x0 | x1 | ... | xn |
| f(x) | y0 | y1 | ... | yn |
Кроме того, пусть задана некоторая точка c 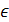 [a,b].
[a,b].
Построим по таблице многочлен Лагранжа:
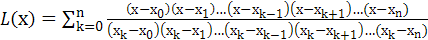 . (20)
. (20)
Если функция f(x) задана своей таблицей и требуется найти значение f(x) где-то в промежуточной точке c, то можно по формуле (20) построить многочлен Лагранжа и его значение в этой точке принять за значение функции
Практическая часть
Задание 1. Построить многочлен Лагранжа и вычислить его значение в указанных точках.
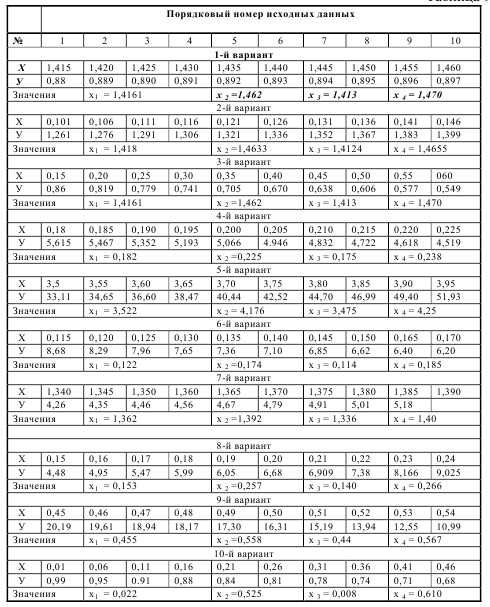
Задание 2.По таблице задания 1 построить многочлен Ньютона и найти значение в указанных точках.
Задание 3. Для функции, заданной таблицей в задании 1, найти значение производной первого и второго порядков в указанных точках.
Задание 4.Для таблицы метода наименьших квадратов построить квадратичное приближение.
Вопросы к защите лабораторной работы №4
«Приближение функций. Численное дифференцирование»
1. Постановка задач приближения функций.
2. Полиномиальная интерполяция. Многочлен в форме Лагранжа.
3. Многочлен в форме Ньютона.
4. Погрешность интерполяции.
5. Интерполяция с кратными узлами.
6. Метод наименьших квадратов.
7. Численное дифференцирование на основе интерполяции.
ЛАБОРАТОРНАЯ РАБОТА №5
Численное интегрирование
Теоретическая часть
Постановка задачи численного интегрирования.Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой. Обычный прием механической квадратуры состоит в том, что данную функцию f(x) на рассматриваемом отрезке [a, b] заменяют интерполирующей или аппроксимирующей функцией φ(x) простого вида, а затем приближенно полагают: 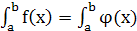 Функция φ(x) должна быть такова, чтобы интеграл
Функция φ(x) должна быть такова, чтобы интеграл 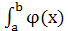 вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности.
вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности.
Составные квадратурные формулы.Приведем ряд простейших квадратурных формул, используемых в практике численного интегрирования функции f(x) на некотором интервале [a, b], разбитого на n равных отрезков точками a0=a, a1=a+h, a2=a+2h, …, an=a+nh+b, где n=0,1, …, k и 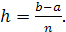 Положим f(xn)=yn=f(a+nh).
Положим f(xn)=yn=f(a+nh).
Формула прямоугольников:
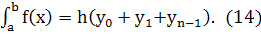
Погрешность формулы определяется выражением:
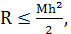 где
где 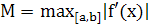 . (15)
. (15)
Формула трапеций:
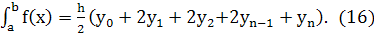
Погрешность формулы определяется выражением:
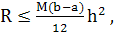 где
где 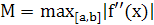 . (17)
. (17)
Формула Симпсона:
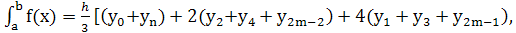
где 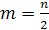 . (18)
. (18)
Погрешность формулы определяется выражением:
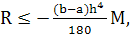 где
где 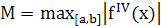 . (19)
. (19)
Практическая часть
Задание 1.Вычислить интеграл 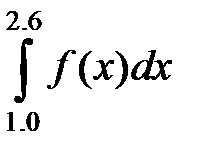 , используя квадратурные формулы:
, используя квадратурные формулы:
а) прямоугольников (левых, правых)с шагом 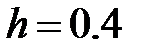 ; дать априорную оценку погрешности;
; дать априорную оценку погрешности;
б) трапеций с шагами 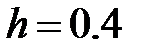 и
и 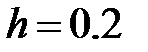 ; оценить погрешность результата по формуле Рунге и уточнить результат по Рунге;
; оценить погрешность результата по формуле Рунге и уточнить результат по Рунге;
в) Симпсона с шагом 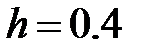 .
.
Промежуточные результаты вычислять с шестью значащими цифрами. Аргументы тригонометрических функций вычислять в радианах.
Образец решения:
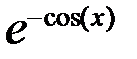 | 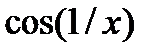 | 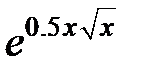 |
а) 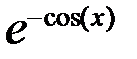
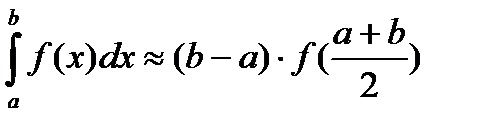
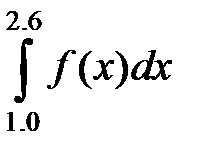
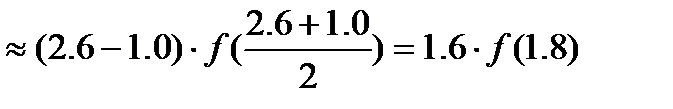
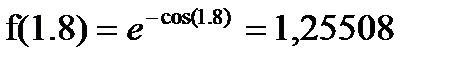
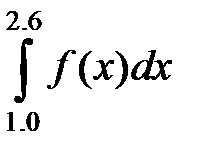
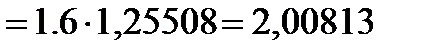
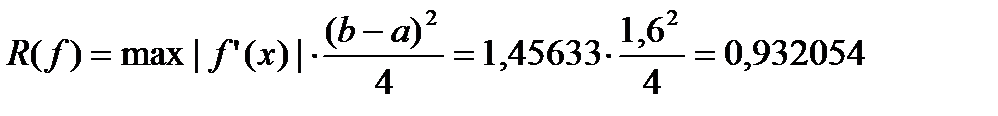
| x | y | y' | |
| 0,582572 | 0,490218 | ||
| 1,4 | 0,843693 | 0,831417 | |
| 1,8 | 1,255083 | 1,22226 | |
| 2,2 | 1,801286 | 1,456334 | |
| 2,6 | 2,35582 | 1,214428 |
а)метод прямоугольника
| Метод прямоугольника | |
| Прав | Лев |
| 2,502352897 | 1,793054 |
| 2,147703371 |
Iправ=0,4*(∑ (y1: y4))= 2,50235
Iлев =0,4*(∑ (y0: y5))= 1,79305
Iобщ =(Iправ+ Iлев)/2= 2,147703371
Оценим погрешность
|Rn|≤M1* 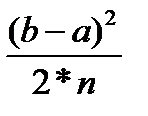
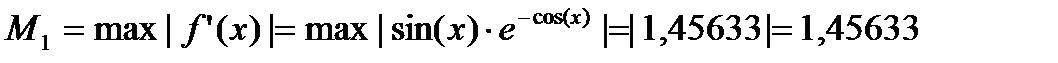
|Rn|≤1,456334*0,256=0,372822
б) 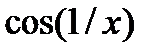
метод трапеций:
h=0.4
| x | y |
| 0,540302 | |
| 1,4 | 0,755561 |
| 1,8 | 0,849608 |
| 2,2 | 0,898461 |
| 2,6 | 0,926943 |
Iтр1=0,4*((y0+ y5)/2+∑( y1: y4))= 1,29490
.
h=0.2
| x | y |
| 0,540302 | |
| 1,2 | 0,672412 |
| 1,4 | 0,755561 |
| 1,6 | 0,810963 |
| 1,8 | 0,849608 |
| 0,877583 | |
| 2,2 | 0,898461 |
| 2,4 | 0,914443 |
| 2,6 | 0,926943 |
Iтр2=0,2*((y0+ y8)/2+∑( y1: y7))= 1,30253
оценим погрешность результата по формуле Рунге
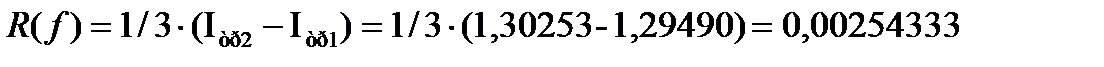
уточним результат по формуле Рунге
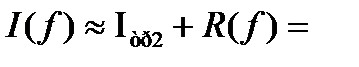 1,30253+0,00254333=1,30507333
1,30253+0,00254333=1,30507333
в) 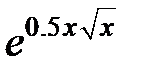
Iсимп =0,4/3*( y0+ y4+4*( y1+ y3)+2*( y2))= 6,14381.
