Расчет силы сопротивления движению плота при его буксировке

Рассчитать силу сопротивления воды движению плота при его буксировке с равномерной скоростью на оптимальной длине буксируемого троса на больших глубинах и спокойной воде по следующим зависимостям:

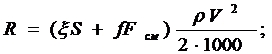
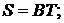
где R ­- сила сопротивления воды движению плота, кН;

S- погруженная в воду площадь поперечного сечения плота, м²;

x -расчетный коэффициент лобового сопротивления, зависящий от отношения ширины плота Вк его осадке Т, таблица 6 ;

F_см - смоченная поверхность плота, м²;

f -расчетный коэффициент сопротивления трения, f = 0,009;

r - плотность воды r = 1000 кг/м³;

V- скорость движения плота в воде или скорость обтекания плота на стоянке, м/с;

L - длина плота, м.

Таблица 6

k = B/T
x	1,10	1,40	1,55	1,72	1,80	1,88	1,96

Значения коэффициента x, отличные от табличных значений, необходимо вычислять, пользуясь методами интерполяции.

Найти зависимости силы сопротивления движению плота от независимых величин B, T, L и V. В таблице результатов предусмотреть графу x.

Исходные данные

В, м	Т, м	L, м	V, м/с
18, 27	1,8; 2; 2,5	120, 240	0,8; 1; 1,2

Значения коэффициента x, отличные от табличных значений, можно вычислить по формуле линейной интерполяции

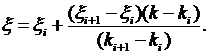
Расчет оптимального срока службы бензиномоторной пилы

Определить оптимальный срок служения бензомоторной пилы МП-5 «Урал-2», используемой на валке леса, по затратам на ремонт в зависимости от времени наработки.

Затраты на ремонт (Y, тыс. руб.) в зависимости от времени наработки (t, час.) аппроксимируются зависимостью вида:

Оптимальный срок службы пилы (T₀) вычисляется по формуле

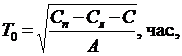
где С - затраты на заработную плату основных рабочих, стоимость израсходованных горюче-смазочных материалов и накладные расходы, тыс. руб.;

С_п- стоимость пилы, тыс. руб.;

С_л - стоимость лома, тыс. руб.

Коэффициенты А, В и С найти методом квадратичной аппроксимации для всех пяти, в зависимости от условий эксплуатации, вариантов исходных данных. Вывести таблицу результатов, содержащую графы: номер варианта, А, В, С, T₀. Построить точечный график и полученную параболу для первого набора исходных данных.

Исходные данные

Стоимость пилы С_п = 175 тыс. руб., стоимость лома C_л = 10 тыс. руб.

	t, час.	Y, тыс. руб. в зависимости от условий эксплуатации
		0,67	0,90	1,02	1,46	3,06
		1,77	1,96	2,29	2,66	6,01
		3,26	3,42	3,98	4,17	10,08
		5,18	5,80	6,21	6,60	16,10
		9,26	10,20	12,76	12,45	26,32
		18,84	21,48	21,64	24,66	48,40
		30,88	37,64	39,46	44,75	78,38
		46,09	52,68	63,46	84,51	116,82
		80,16	93,34	109,58	147,84	184,67

Для решения задачи квадратичной аппроксимации можно использовать следующие выражения:

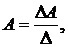
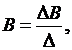
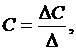
где определитель системы

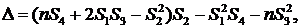
определители неизвестных:

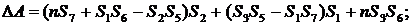
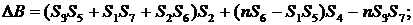
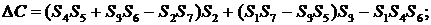
суммы:

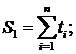
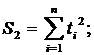
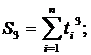
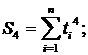
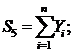
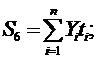
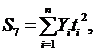
где n - количество точек, n = 9.

Определение диаметра трубы

Определить диаметр трубы, соединяющей озеро и колодец, если вода движется самотеком.

Диаметр трубы (d, м) определяется уравнением высокого порядка

Ad⁶ - Cd² - Bd - E=0, (4)

где

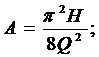
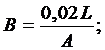
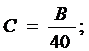
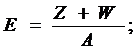
где H - напор воды;

Q - расход воды;

L - длина трубы;

Z и W - коэффициенты местных потерь.

Найти зависимость d от независимых переменных H, Q и L.

Исходные данные

Hmin	Hmax	DH	Qmin	Qmax	DQ	L	Z	W
			0,01	0,05	0,01	100; 150

Для уточнения корня уравнения высокого порядка можно использовать метод касательных (Ньютона):

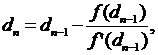
где n - номер итерации, n = 1, 2, 3, ...;

f(d_n-1) - значение функции, левой части уравнения (4), при очередном приближении;

f¢(d_n-1) - значение первой производной функции при очередном приближении.

Условие окончания вычислений

ïd_n – d_n-1ï £ e,

где e - точность вычислений, e = 10 ^-5.

Начать уточнение корня с d₀ = 0,2 м.