Расчет и построение временных характеристик аналогового фильтра

Временными характеристиками цепи называются откликами на типовые составляющие исходного сигнала.

Переходная характеристика цепи - это отклик цепи с нулевыми начальными условиями на воздействие единичной функции (функции Хевисайда). Переходная характеристика определяется из операторной передаточной функции путем её деления на оператор , и нахождения оригинала от получившегося изображения с помощью обратного преобразования Лапласа через вычеты.

Импульсная характеристика цепи – это отклик цепи на воздействие дельта-функции . – бесконечно короткий по длительности и бесконечно большой по амплитуде импульс единичной площади. Импульсная характеристика определяется путем нахождения вычетов от передаточной функции цепи.

Временные характеристики цепи будем искать также операторным методом. Для этого нужно найти операторное изображение входного сигнала, умножить его на коэффициент передачи в операторной форме и от полученного выражения найти оригинал, т. е зная коэффициент передачи цепи, мы можем найти отклик на любое воздействие.

Нахождение импульсной характеристики сводится к нахождению реакции цепи на дельта-функцию. Известно, что для дельта-функции изображением является 1. Применяя обратное преобразование Лапласа, найдем импульсную характеристику.

Выделим целую часть для передаточной функции цепи, так как степени старших коэффициентов в числителе и в знаменателе равны:

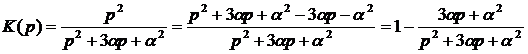
Найдем особые точки передаточной функции, приравняв знаменатель к нулю.

.

Имеем всего одну особую точку, теперь берем вычет в этой особой точке.

.

.

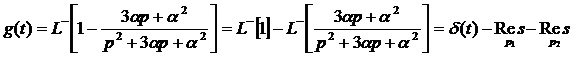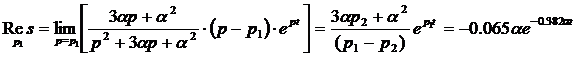Выражение для импульсной характеристики запишется следующим образом:

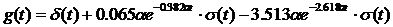
Аналогично найдем переходную характеристику цепи, зная, что для функции Хевисайда изображением является функция .

;

;

;

)

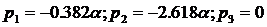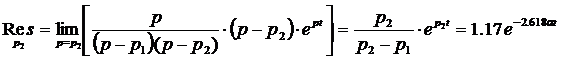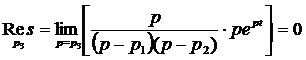
Переходная и импульсная характеристики связаны между собой, так же как и входные воздействия :

;

;

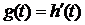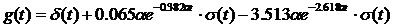
Учитывая нормировку 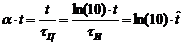, запишем конечные формулы для временных характеристик:

;

.

Построим графики этих функций:

Рисунок 2.5 – Импульсная характеристика

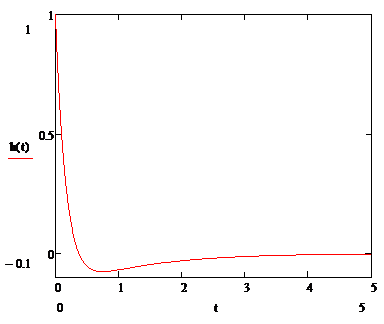
Рисунок 2.6 – Переходная характеристика

Временные характеристики существуют только при 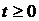, так как отклики не могут опережать воздействия.

Наша цепь является дифференцирующей, поэтому переходная характеристика ведет себя так. Дифференцирующая цепь заостряет переходный процесс и пропускает передний фронт. За «бросок» отвечают прошедшие высокие частоты, а за завал – не прошедшие низкие частоты.
2.4 РАСЧЕТ И ПОСТРОЕНИЕ ПЕРИОДИЧЕСКОГО СИГНАЛА ЧЕРЕЗ АНАЛОГОВУЮ ЛИНЕЙНУЮ ЭЛЕКТРИЧЕСКУЮ ЦЕПЬ

Периодический сигнал, проходя через ЛЭЦ, не теряет своей периодической природы, поэтому сигналы на входе и выходе цепи можно представить бесконечной суммой непериодических сигналов, сдвинутых друг от другу на период. Для расчета прохождение периодического сигнала через ЛЭЦ используем метод комплексных амплитуд, зная передаточную функцию цепи .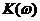

Постоянная составляющая на выходе прямо пропорциональна значению коэффициента передачи при 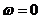. Амплитуды гармонических колебаний умножаются на значения модуля передаточной функции на частотах . Начальные фазы гармонических колебаний суммируются со значениями фазочастотной характеристики ЛЭЦ на частотах .

,

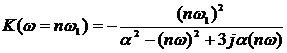Периодический сигнал на выходе ЛЭЦ описывается рядом:

Изобразим графически отклик для периодического сигнала:

Рисунок 2.7 – Периодический сигнал на выходе ЛЭЦ по 26 гармоническим колебаниям

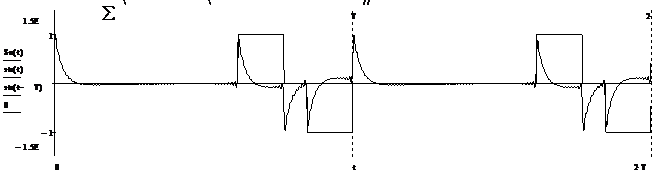
Рисунок 2.8 – Периодический сигнал на выходе ЛЭЦ по 100 гармоническим колебаниям

На рисунке наблюдаем, что при увеличении числа рассматриваемых гармоник «бросок» становится более четким, т. е. исчезает пульсирующий характер.

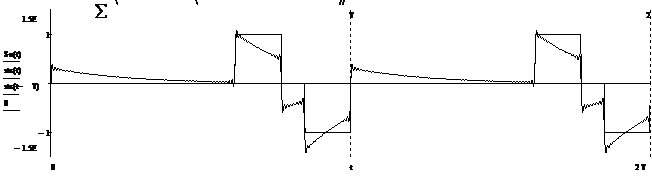
Рисунок 2.9 – Периодический сигнал на выходе ЛЭЦ при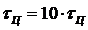

Рисунок 2.10 – Периодический сигнал на выходе ЛЭЦ при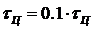

Анализируя полученные графики можно сказать, что с увеличением 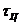отклик становится более похожим на входной сигнал.