Спектральный анализ аналоговых периодических и непереодичеких сигналов
СПЕКТРАЛЬНЫЙ АНАЛИЗ АНАЛОГОВЫХ ПЕРИОДИЧЕСКИХ И НЕПЕРЕОДИЧЕКИХ СИГНАЛОВ
ИСХОДНЫЕ ДАННЫЕ
Известны следующие исходные данные:
· Код сигнала: 76
· E=1B – амплитуда импульса;
· Tос=1300 мкс – период описания сигнала;
· τи=200 мкс – длительность импульса.
Рисунок 1.1 –Временное представление аналогового сигнала
РАЗЛОЖЕНИЕ СИГНАЛА НА ТИПОВЫЕ СОСТАВЛЯЮЩИЕ
Исходя из временного представления сигнала (рисунок 1.1), разложим его на типовые составляющие, включающиеся в определенный момент времени. Для этого используем единичную функцию включения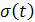 
.
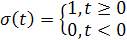
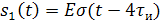
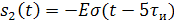
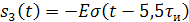
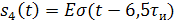
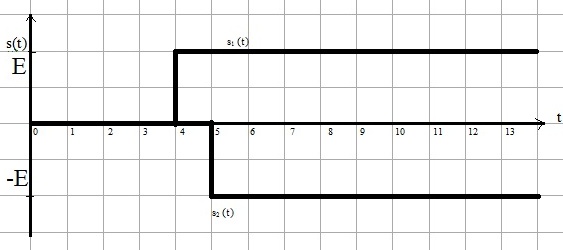
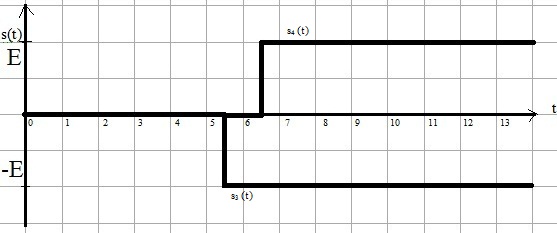
Рисунок 1.2 – Временное представление типовых составляющих аналогового сигнала
РАСЧЕТ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ АНАЛОГОВОГО СИГНАЛА
Спектральной характеристикой (или спектральной плотностью) непериодического сигнала называют комплексную функцию частоты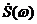 
:
.
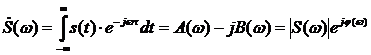1. Рассмотрим одиночный импульс нашего сигнала (рисунок 1.3).
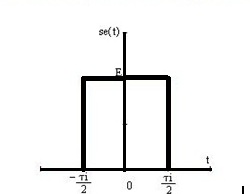
Рисунок 1.3 – Временное представление одиночного импульса
2. Представим сигнал с помощью элементарных составляющих (рисунок 1.4).
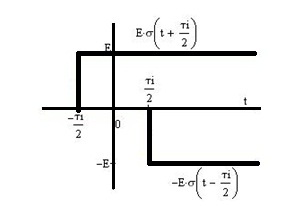
Рисунок 1.4 - Временное представление сигнала с помощью элементарных составляющих
3. Применяя прямое преобразование Лапласа, получим:
.
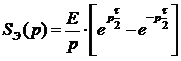4. Заменяя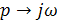 
, перейдем к спектральной плотности элементарной составляющей сигнала:
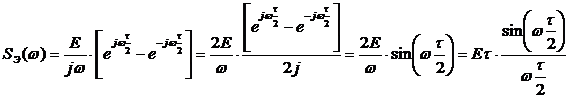
5. Моделируем сигнал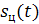 
от 
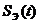(рисунок 1.4):
.
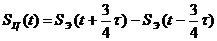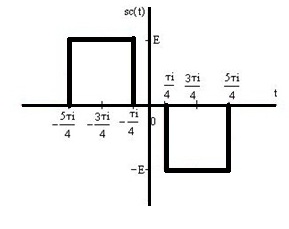
Рисунок 1.5 – Временное представление центрированного сигнала
6. Применяя прямое преобразование Лапласа, получим спектральную плотность центрированного сигнала:
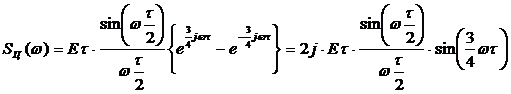
7. Возвращая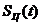 
в исходное место, получим конечное выражение для расчета спектральной плотности:
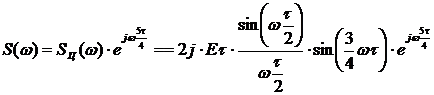
Построение частотных характеристик аналогового сигнала
Модуль комплексной спектральной плотности называют амплитудно-частотной характеристикой (АЧХ) спектра сигнала s(t). Аргумент комплексной спектральной плотности фазочастотной характеристикой (ФЧХ) спектра сигнала s(t).
Построим графики с нормированными значениями, применив замену:
t н = t/τi
αt = ln10* t н = 2,3 * t н
ω н = ω/α
ωτ = ω н * ln 10 = ω* 2.3
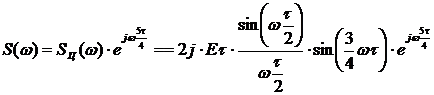
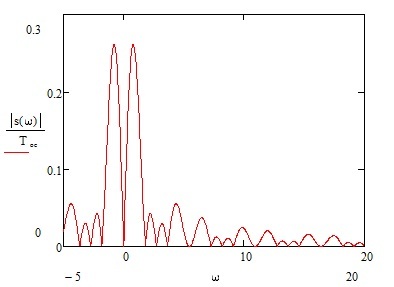
Рисунок 1.6 – АЧХ аналогового сигнала
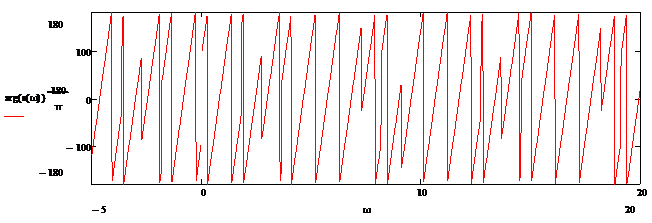
Рисунок 1.7 - ФЧХ аналогового сигнала
РАСЧЕТ И ПОСТРОЕНИЕ СПЕКТРА КОЭФФИЦИЕНТОВ КОМПЛЕКСНОГО РЯДА ФУРЬЕ
Ряд Фурье – это разложение периодического сигнала по тригонометрическим либо комплексным функциям.
Найдем коэффициенты комплексного ряда Фурье с помощью дискретизации спектральной плотности аналогового сигнала.
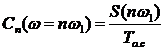
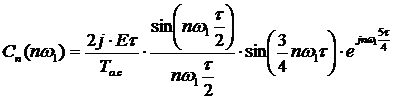, где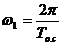 
- циклическая частота сигнала.
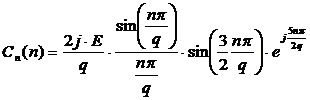, где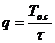 
– скважность.
Построим спектральные характеристики периодического сигнала.
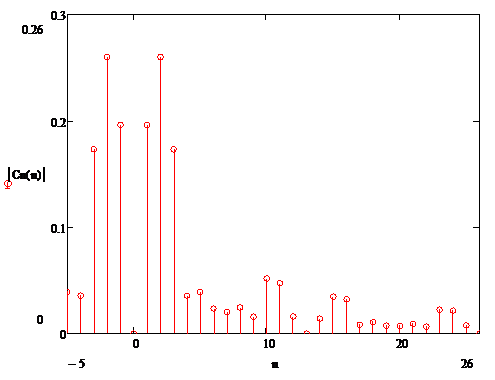
Рисунок 1.8 – Спектр амплитуд коэффициентов комплексного ряда Фурье
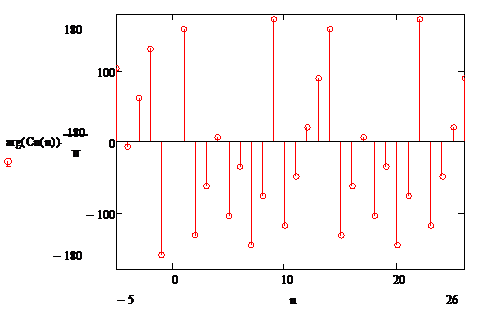
Рисунок 1.9– Спектр фаз коэффициентов комплексного ряда Фурье
Таблица 1 – Коэффициенты комплексного ряда Фурье
| N | Алгебраическое представление С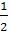n =  (an-jbn) | Модуль |Cn| | Аргумент Arg(Cn) |
| - | |||
| -0.183 + j0.07 | 0.196 | ||
| -0.172 - j0.195 | 0.26 | -132 | |
| 0.081 - j0.154 | 0.173 | -62 | |
| 0.035 + j4.293*10-3 | 0.036 | ||
| -9.39*10-3 - j0.038 | 0.039 | -104 | |
| 0.02 - j0.013 | 0.024 | -35 | |
| -0.017 - j0.012 | 0.02 | -145 | |
| 5.869*10-3 - j0.024 | 0.025 | -76 | |
| -0.016 + j1.908*10-3 | 0.016 | ||
| -0.024 - j0.046 | 0.052 | -118 | |
| 0.031 - j0.035 | 0.047 | -49 | |
| 0.015 + j5.797*10-3 | 0.016 | ||
| -90 | |||
| -0.013 + j4.969*10-3 | 0.014 | ||
| -0.023 - j0.026 | 0.035 | -132 | |
| 0.015 - j0.029 | 0.033 | -62 | |
| 8.318*10-3 + j1.01*10-3 | 8.38*10-3 | ||
| -2.608*10-3 - j0.011 | 0.011 | -104 | |
| 6.17*10-3 - j4.259*10-3 | 7.498*10-3 | -35 | |
| -5.862*10-3 - j4.046*10-3 | 7.123*10-3 | -145 | |
| 2.236*10-3 - j9.071*10-3 | 9.342*10-3 | -76 | |
| -6.42810-3 + j7.805*10-4 | 6.475*10-3 | ||
| -0.011 - j0.02 | 0.023 | -118 | |
| 0.014 - j0.016 | 0.022 | -49 | |
| 7.337*10-3 + 2.783*10-3 | 7.847*10-3 | ||
| -90 |
АНАЛИЗ АНАЛОГОВОЙ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ИСХОДНЫЕ ДАННЫЕ
Табличное представление исходных данных:
| № варианта | № бригады | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 | №схемы |
| 3 (26) | pL | R | pL | R | R | R |
Рисунок 2.1 – Исходная схема аналогового фильтра
Заключение
В ходе курсовой работы в первой части был произведен спектральный анализ аналоговых непериодического и периодического сигналов. С помощью единичной функции включения разложили сигнал на его типовые составляющие, которые включаются в определенный момент времени. Рассчитали изображение по Лапласу, когда находили спектральную плотность аналогового непериодического сигнала, на основе которого рассчитали коэффициенты комплексного ряда Фурье, описывающего аналоговый периодический сигнал. Сигнал представлял собой знакочередующуюся последовательность импульсов прямоугольной формы, из-за чего постоянная составляющая комплексного ряда Фурье оказалась равной нулю. Построили спектральные характеристики аналогового периодического сигнала. Обнаружили, что с ростом количества гармоник амплитуды убывают, форма огибающей спектральных составляющих имеет лепестковый характер. Задав пороговый критерий равной десятой части амплитуды максимальной гармоники, нашли ширину спектра сигнала. Восстановили периодический сигнал усечённым рядом Фурье по двадцати шести гармоникам. Построенный график давал возможность судить о форме и свойствах сигнала. Периодизация сигнала произошла из-за дискретизации спектральной плотности в частотной области, а пульсировал восстановленный сигнал из-за ограниченной двадцатью шестью гармониками ширины спектра сигнала. При увеличении числа гармоник восстановленный сигнал становился все более похожим на исходный аналоговый сигнал. Рассчитали и построили погрешность представления аналогового периодического сигнала усечённым рядом Фурье, равная 
.
Во второй части курсовой работы произвели анализ аналоговой линейной электрической цепи во временной и частотной области. Для заданной цепи нашли операторное выражение передаточной функции, от которого перешли к комплексному коэффициенту передачи, заменив в полученном выражении операторную переменную 
на множитель 
. Рассчитали и построили амплитудно-частотную, фазочастотную характеристики, взяв модуль и аргумент соответственно от комплексного коэффициента передачи. Также были рассчитаны и построены переходная и импульсная характеристики операторным методом расчёта. Используя метод комплексных амплитуд, нашли прохождение периодического сигнала через аналоговую линейную электрическую цепь. Также рассчитали прохождение непериодического сигнала через заданную цепь, представив входной сигнал как сумму единичных воздействий. Вследствие чего на выходе мы получили сумму переходных характеристик исследуемой цепи с учетом весов и сдвигов по времени. Для прохождений периодического и непериодического сигнала через цепь были построены отклики. Увидели, что отклик непериодического сигнала на выходе линейной электрической цепи подобен периодическому сигналу, построенный по большому количеству гармоник.
Список использованной литературы
1. Баскаков С. И. Радиотехнические цепи и сигналы. М.: Высш. школа, 2005. – 462 с. (304 экз.) ISBN: 5-06-003843-2.
2. Каратаева Н. А. Радиотехнические цепи и сигналы. Теория сигналов и линейные цепи. Учебное пособие. Томск: ТУСУР, 2012. – 261 с. Режим доступа: http://edu.tusur.ru/training/publicatos/2798.
3. Каратаева Н. А. Радиотехнические цепи и сигналы. Теория сигналов и линейные цепи. Учебное пособие. Томск: ТУСУР, 2003. – 255 с. (108 экз.) ISBN 5-86889-175-9.
4. Учебное методическое пособие. Радиотехнические цепи и сигналы. Часть 1. Теория сигналов и линейные цепи. Каратаева Н. А, Киселев П. Томск: ТУСУР, 2012. – 33 с. Режим доступа: http://edu.tusur.ru/training/publicatos/2790.
СПЕКТРАЛЬНЫЙ АНАЛИЗ АНАЛОГОВЫХ ПЕРИОДИЧЕСКИХ И НЕПЕРЕОДИЧЕКИХ СИГНАЛОВ
ИСХОДНЫЕ ДАННЫЕ
Известны следующие исходные данные:
· Код сигнала: 76
· E=1B – амплитуда импульса;
· Tос=1300 мкс – период описания сигнала;
· τи=200 мкс – длительность импульса.
Рисунок 1.1 –Временное представление аналогового сигнала