Алгебраический момент силы относительно точки

При изучении плоских систем сил рассматривают алгебраический момент силы относительно моментной точки, лежащей в плоскости действия сил.

Алгебраическим моментом силы относительно точки называется взятое со знаком плюс или минус произведение модуля силы на ее плечо относительно моментной точки. Знак плюс выбирается, если сила стремится повернуть тело вокруг моментной точки против движения часовой стрелки.

Вычисление алгебраического момента силы поясняется на рис. 69. В соответствии с рисунком для алгебраических моментов силы 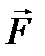относительно точек А, В и С имеем

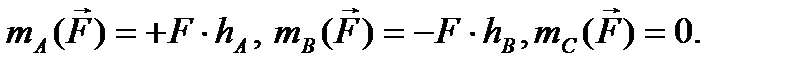(65)

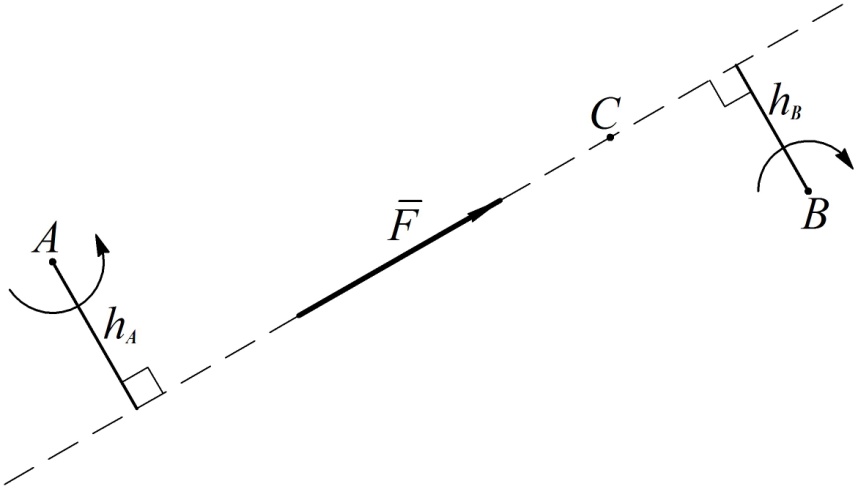
Рис. 69

Отметим, что алгебраический момент силы относительно точки равен моменту силы относительно оси, проведенной перпендикулярно плоскости действия сил к нам. По указанным выше правилам можно вычислять векторный, относительно оси и алгебраический моменты не только для вектора силы, но и для любого другого вектора.

Глава 4. ПАРА СИЛ И ЕЕ СВОЙСТВА

Понятие о паре сил

Парой сил называется система из двух равных по величине сил, направленных в противоположные стороны вдоль параллельных прямых.

Пара сил – это неупрощаемая система сил (её действие на тело нельзя эквивалентным образом заменить действием одной равнодействующей силы). Она стремится придать телу вращательное движение из состояния покоя. Пару сил в механике рассматривают как одно из основных понятий наряду с понятием силы. Действие пары сил на тело характеризуется её векторным моментом.

Векторным моментом пары сил называется вектор, равный по величине произведению модуля одной из сил пары на плечо пары сил. Векторный момент пары сил направлен перпендикулярно плоскости действия пары сил по правилу правого винта (в ту сторону, откуда видно, что пара сил стремится повернуть тело против часовой стрелки).

Плечом h пары сил называется расстояние между линиями действия сил, составляющих пару.

Схематически пара сил и её векторный момент показаны на рис. 70.

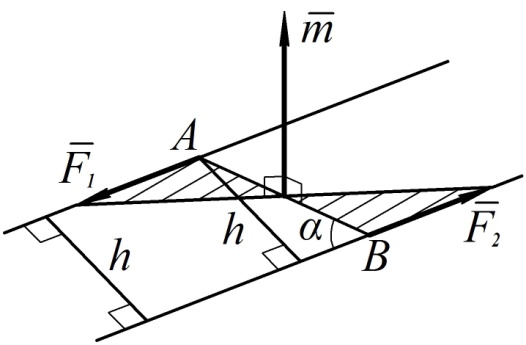
Рис. 70

Модуль векторного момента в соответствии с данным определением вычисляется по формуле

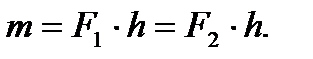(66)

Можно доказать, что пара сил, приложенная к твердому телу, обладает следующими свойствами.

Легко доказать, что векторный момент пары сил можно выразить в виде векторного произведения по формуле (см. рис. 69)

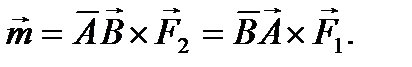(67)

Действительно, модуль такого векторного произведения

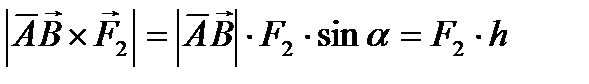
совпадает с величиной векторного момента (см. формулу (66)). Направление каждого из векторных произведений в (67) тоже совпадает с направлением векторного момента пары сил (см. рис. 70).

При рассмотрении плоских систем сил, в состав которых входят пары сил, вводится понятие алгебраического момента пары сил.

Алгебраическим моментом пары сил называется взятое со знаком плюс или минус произведение модуля одной из сил пары на плечо пары сил. Знак алгебраического момента пары сил определяется по правилу правого винта (момент считается положительным, если пара сил стремится повернуть тело против часовой стрелки).

Таким образом, алгебраический момент пары сил может быть вычислен по формуле

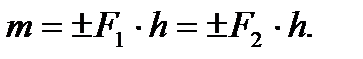(68)

На рисунках и расчетных схемах пару сил обозначают либо её векторным моментом, либо одним из значков, показанных на рис. 71, расположенным в плоскости действия пары сил.

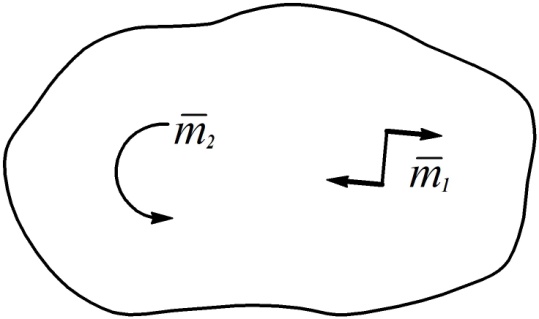
Рис. 71

Основные свойства пар сил

Можно доказать, что пара сил, приложенная к твердому телу, обладает следующими свойствами.

1. Пару сил, не изменяя её действия на тело, можно как угодно поворачивать и переносить в плоскости её действия в пределах тела.

2.Пару сил, не изменяя её действия на тело, можно переносить в пределах тела из плоскости её действия в параллельную плоскость.

3. Не изменяя действия пары сил на тело, можно одновременно изменять величину сил пары и её плечо так, чтобы величина её момента оставалась неизменной.

Отсюда следует, что действие пары сил на тело полностью характеризуется её векторным моментом.

Докажем далее две важные теоремы о свойствах пар сил.

Теорема о сложении пар сил

Две пары сил, действующие на твердое тело, можно эквивалентным образом заменить одной парой сил, векторный момент которой равен геометрической сумме векторных моментов исходных пар сил.

Доказательство

Пусть имеется две пары сил 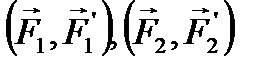, лежащие в пересекающихся плоскостях (см. рис. 72).

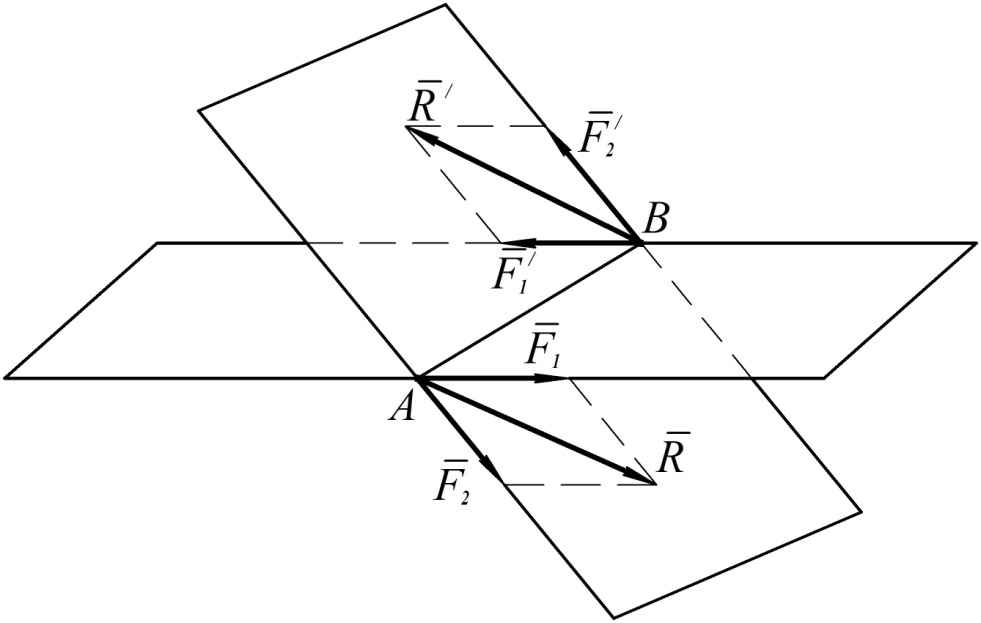
Рис. 72

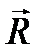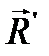Такие пары сил можно получить из пар сил, как угодно расположенных в пересекающихся плоскостях, путем параллельного переноса, поворота в плоскости действия и одновременного изменения плеч и величин сил пар. Сложим геометрически силы в точках А и В. Получим две силы и , эквивалентные исходным четырем силам. Силы 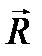и 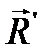составляют пару сил, так как

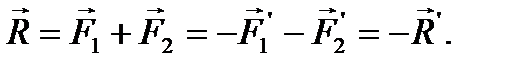
Моменты исходных пар сил можно выразить в виде векторных произведений

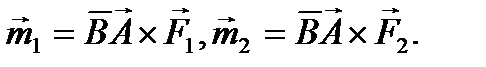
Для момента эквивалентной пары сил можно записать

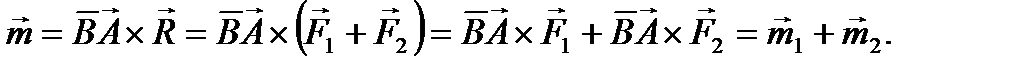
Теорема доказана.

Применяя последовательно эту теорему, можно любое количество пар сил заменить одной эквивалентной парой сил, векторный момент которой равен геометрической сумме векторных моментов исходных пар сил.

Теорема о сумме моментов сил пары

Геометрическая сумма векторных моментов сил, составляющих пару, относительно любой точки пространства равна векторному моменту пары сил.

Доказательство

Изобразим пару сил на рис. 73 и вычислим геометрическую сумму векторных моментов сил 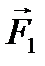и 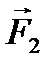относительно произвольно выбранной точки О

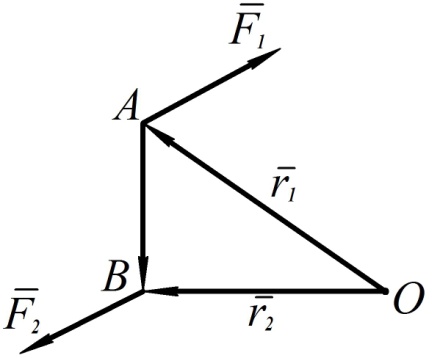
Рис. 73

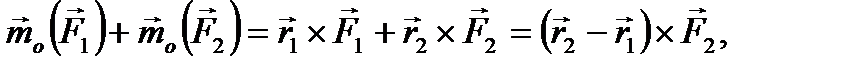
так как для пары сил 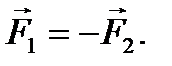Кроме того, 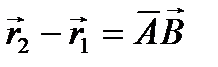независимо от выбора точки

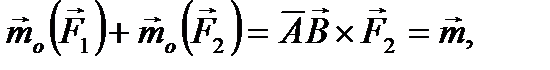
что и требовалось доказать.

Отметим, что при рассмотрении пар сил, расположенных в одной плоскости, в формулировках двух последних теорем следует векторные моменты заменить на алгебраические.