Непрерывность и точки разрыва функции.

Предел последовательности.

Опр.1. Пусть 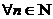поставлено в соответствие вполне определенное число a 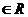(причем различным n могут соответствовать одинаковые числа). Совокупность элементов a , n=1,2,3… называется числовой последовательностью, каждый элемент a - элементом (членом) последовательности, n-его номер.

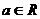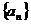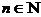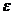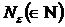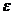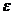Опр.2. Число называется пределом последовательности , , если для любого сколь угодно малого действительного положительного , найдется такой номер , зависящий от , что |a -a|< при 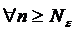.В этом случае пишут 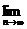а =а или а 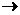а при n .

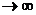Опр.3. Последовательность 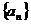, n 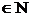,называется ограниченной, если существует действительное число с>0 , что |a |<c при .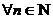

Пример 1. Зная несколько первых членов последовательности, написать одно из возможных выражений для общего члена:

; ; ; ; ;…

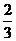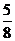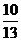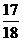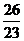Решение: числитель каждого из заданных членов последовательности равен квадрату номера этого члена плюс единица, т.е. n 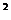+1. Знаменатели образуют арифметическую прогрессию 3,8,13,18…. с первым членом x 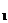=3 и разностью d=5. Поэтому x =x 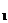+d(n-1)=5n-2.

Следовательно, исходная формула а = .

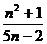ЗАМЕЧАНИЕ: знание нескольких первых членов последовательности еще не определяет эту последовательность.

Пример 2. Доказать, что последовательность а =(-1) 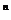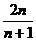sin n ограничена.

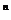
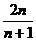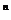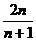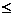
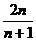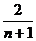Решение: |а |=|(-1) sin n|=|(-1) | | | |sin n| =2- <2,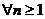

Отсюда, по опр.3. а -ограничена, с=2.

Пример 3. Непосредственно доказать, что при ,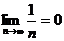

Решение: Необходимо доказать, что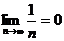

Пример 4. Пользуясь опр.2., доказать, что 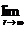а = 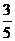, если а = 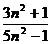, начиная с какого n выполняется неравенство

| а - 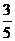| <0,01.

Решение: найдем | а - | = | - | = .

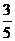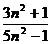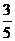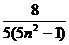Пусть 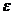>0 задано. Выберем так, чтобы выполнялось неравенство < .

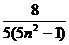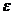Решаем это неравенство: в силу 17 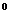действительных чисел, будем иметь 5 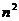-1> > .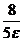

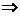
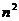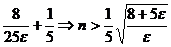Положив 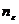= [ 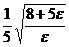]+1, получим, что при 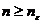, |a - |< .

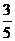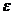А это означает в силу опр.2. 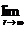а = 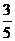. Пусть 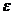=0,01, тогда n 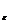=[ 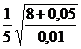]+1= [ 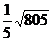]+1=6 и все члены последовательности, начиная с шестого, содержатся в U( 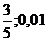) – окрестности точки 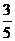, т.е. в интервале ] 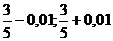[ =]0,59;0,61[.

Вычисление предела последовательности.

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся. Для сходящихся последовательностей справедливы теоремы, вытекающие из определения предела:

1.

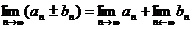
2.

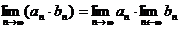
3.

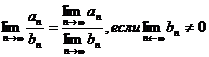
Пример 1. Найти предел: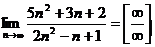

Как показывает решение задачи, подстановка предельного значения приводит к неопределенности 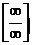. Часто встречаются неопределенности вида 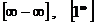. Нахождение предела последовательности в этих случаях называют раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразования данного выражения.

Решение примера 1: Поделим числитель и знаменатель на наивысшую степень n, в данном случае на n :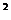

.

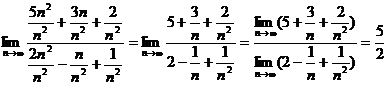Т.к. 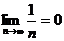(см. пр.3 Л.р.№3).

Пример 2. Найти предел: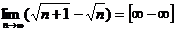

Решение: Умножим и разделим выражение, стоящее под знаком предела на выражение сопряженное ему:

.

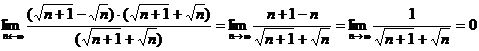Пример 3.Найти предел: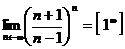

Решение: Воспользуемся 2-м замечательным пределом: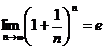

= .

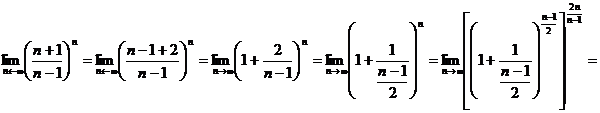
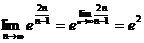Предел функции.

Опр.1.Число 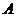называется пределом функци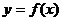и при 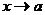, если для любой окрестности 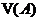числа 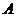существует такая проколотая окрестность 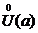числа a, что для всех ,

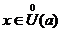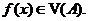
Это определение по Коши. Число 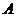может быть как конечным, так и бесконечным. В частности, если числа 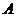и а конечны, получаем следующее определение (на языке “ - ”).

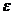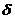Опр.2. Число 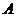называется пределом функци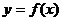и при 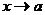, если для всякого 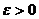существует такое число 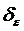>0, что для всех х, удовлетворяющих неравенству 0< 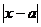< 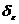и входящих в область определения функции 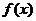, справедливо неравенство:

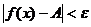(1)

и обозначается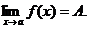

Если а = + 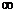, то получаем следующее определение.

Опр.3.Число 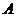называется пределом функци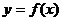и при 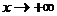, если для всякого 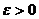существует такое число 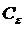>0, что для всех х, удовлетворяющих неравенству 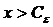и входящих в область определения функции 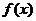, справедливо (1) и обозначается:

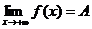(определение “ 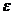-C”).

Определение предела функции по Гейне: Число А называется пределом функции y=f(x) при 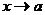(в точке a), если для любой сходящейся к числу а последовательности 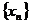значений х, входящих в область определения функции и отличных от a, соответствующая последовательность 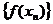этой функции сходится к числу А.

Пример 1. Пользуясь определением предела по Гейне, доказать, что

.

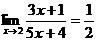Решение: Рассмотрим любую последовательность 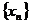, удовлетворяющую двум условиям:

1)

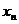
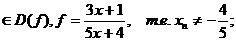
2) .

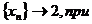
Этой последовательности 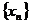соответствует последовательность значений функции:

…

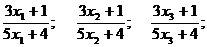Тогда на основании свойств сходящихся последовательностей (каких?) будем иметь

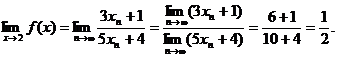
Т.о. независимо от выбора последовательности 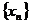, сходящейся к числу 2 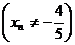, соответствующая последовательность значений функции 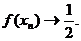А это на основании определения предела функции по Гейне значит, что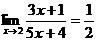

Замечание 1: Определением предела по Гейне удобно пользоваться тогда, когда доказывается, что функция f(x) не имеет предела. Для этого достаточно показать, что существует две последовательности но соответствующие последовательности 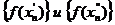имеют неравные пределы.

Пример 2: Доказать, что 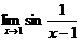не существует.

Решение: возьмем

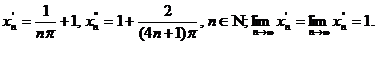
Тогда соответствующие последовательности значений функции таковы:

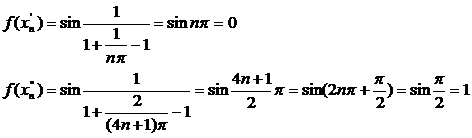
Следовательно,

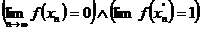, т.е. 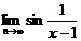не существует

Замечание 2: Пример 2 показывает, что вывод о наличии предела функции нельзя делать, исходя из последовательности {x_n} частного вида (например, исходя из x_n^'' =1+ 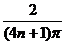), а нужно рассматривать произвольную последовательность {x_n }, имеющую заданный

предел а.

Пример 3: Пользуясь " 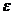– 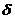" определением предела, доказать, что

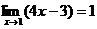
Решение: Надо доказать, что для "e>0 существует такое d_e >0, что из неравенства 0 < |x-1| < d_e следует, что |f(x)-1| < e, f(x)=4x-3. Зададим

e > 0 и рассмотрим выражение: |f (x)-1|=|4x-3-1|= 4|x-1|.

Если взять d_e ≤ e/4, то для всех х, удовлетворяющих неравенству |x-1| < d_e, будем иметь |f(x)-1| = 4|x-1|<4d_e ≤ 4e/4=e.

Следовательно,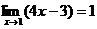

Пример 4: f(x)=1/(x-1) доказать, что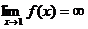

Решение: По определению 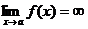, если для " М>0 можно подобрать d_М>0, что для всех х¹а, удовлетворяющих неравенству

0<|x-a|<d, будет выполняться условие 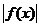>M. В нашем случае по заданному M>0 будем подбирать d_М из условия

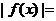| 1/|x-1|>M Ú |x-1|<1/M.

Следовательно, положив d_M=1/М, получим, что для всех х, удовлетворяющих неравенству 0<|x-1|<d_M, выполняется неравенство 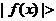M, значит,

Вычисление предела функции.

При вычислении предела функции необходимо знать следующие

теоремы:

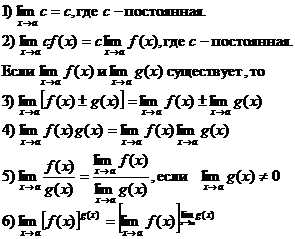
Кроме того, надо пользоваться тем, что для всех основных элементарных функций в любой точке их области определения справедливо равенство:

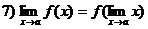(в силу непрерывности, Л.р. №7)

Этими простейшими пределами можно пользоваться как формулами:

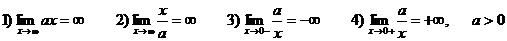
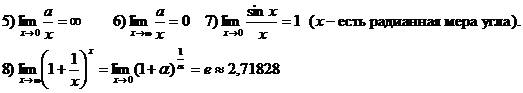
Более сложные случаи нахождения предела функции: 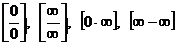,[1^¥] рассматриваются далее в отдельности.

Пример 1.Найти предел:

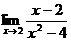
Решение:

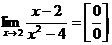
Разлагаем знаменатель на множители:

Здесь нет сокращения на нуль, что никогда недопустимо. Согласно определению предела функции аргумент х стремиться к своему предельному значению 2, никогда с ним не совпадая.

Пример 2. Найти предел:

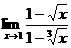
Решение:

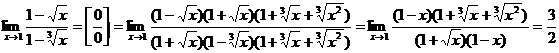Пример 3. Найти предел:

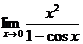
Решение:

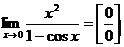
(Применяем тригонометрическую формулу так, чтобы использовать первый замечательный предел).

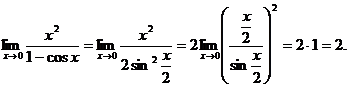
Пример 4. Найти предел:

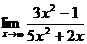
Решение:

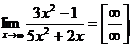
Деля числитель и знаменатель на наивысшую степень х (на х²), находим

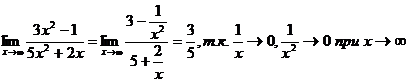
Случай, когда при х®а или х®¥ функция f(x) представляет произведение бесконечно малой величины на бесконечно большую 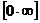, приводится путем преобразования функции к одному из двух рассмотренных случаев, т.е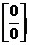. к или к .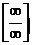

Случай, когда при х®а или х®¥ функция f(x) представляет разность двух положительных бесконечно больших величин 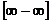, можно привести к случаю 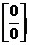или 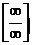путем преобразования функции к дроби.

Пример 5. Найти следующий предел:

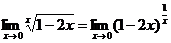
Решение:

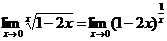
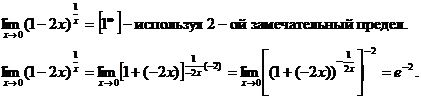
Предел последовательности.

Опр.1. Пусть 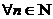поставлено в соответствие вполне определенное число a 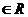(причем различным n могут соответствовать одинаковые числа). Совокупность элементов a , n=1,2,3… называется числовой последовательностью, каждый элемент a - элементом (членом) последовательности, n-его номер.

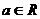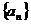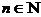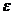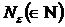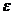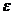Опр.2. Число называется пределом последовательности , , если для любого сколь угодно малого действительного положительного , найдется такой номер , зависящий от , что |a -a|< при 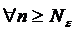.В этом случае пишут 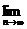а =а или а 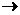а при n .

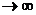Опр.3. Последовательность 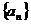, n 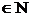,называется ограниченной, если существует действительное число с>0 , что |a |<c при .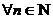

Пример 1. Зная несколько первых членов последовательности, написать одно из возможных выражений для общего члена:

; ; ; ; ;…

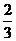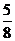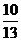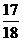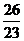Решение: числитель каждого из заданных членов последовательности равен квадрату номера этого члена плюс единица, т.е. n 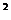+1. Знаменатели образуют арифметическую прогрессию 3,8,13,18…. с первым членом x 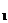=3 и разностью d=5. Поэтому x =x 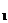+d(n-1)=5n-2.

Следовательно, исходная формула а = .

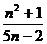ЗАМЕЧАНИЕ: знание нескольких первых членов последовательности еще не определяет эту последовательность.

Пример 2. Доказать, что последовательность а =(-1) 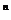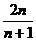sin n ограничена.

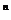
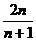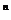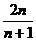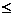
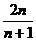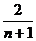Решение: |а |=|(-1) sin n|=|(-1) | | | |sin n| =2- <2,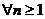

Отсюда, по опр.3. а -ограничена, с=2.

Пример 3. Непосредственно доказать, что при ,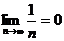

Решение: Необходимо доказать, что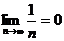

Пример 4. Пользуясь опр.2., доказать, что 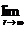а = 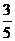, если а = 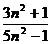, начиная с какого n выполняется неравенство

| а - 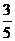| <0,01.

Решение: найдем | а - | = | - | = .

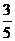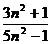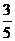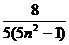Пусть 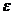>0 задано. Выберем так, чтобы выполнялось неравенство < .

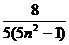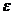Решаем это неравенство: в силу 17 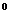действительных чисел, будем иметь 5 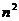-1> > .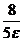

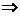
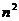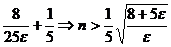Положив 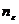= [ 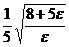]+1, получим, что при 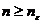, |a - |< .

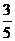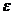А это означает в силу опр.2. 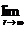а = 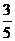. Пусть 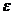=0,01, тогда n 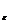=[ 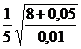]+1= [ 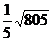]+1=6 и все члены последовательности, начиная с шестого, содержатся в U( 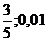) – окрестности точки 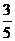, т.е. в интервале ] 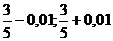[ =]0,59;0,61[.

Вычисление предела последовательности.

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся. Для сходящихся последовательностей справедливы теоремы, вытекающие из определения предела:

1.

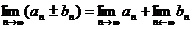
2.

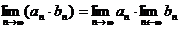
3.

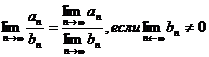
Пример 1. Найти предел: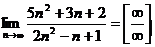

Как показывает решение задачи, подстановка предельного значения приводит к неопределенности 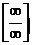. Часто встречаются неопределенности вида 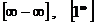. Нахождение предела последовательности в этих случаях называют раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразования данного выражения.

Решение примера 1: Поделим числитель и знаменатель на наивысшую степень n, в данном случае на n :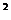

.

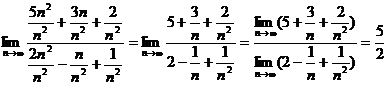Т.к. 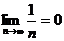(см. пр.3 Л.р.№3).

Пример 2. Найти предел: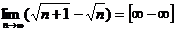

Решение: Умножим и разделим выражение, стоящее под знаком предела на выражение сопряженное ему:

.

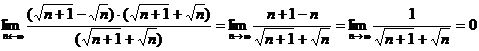Пример 3.Найти предел: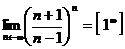

Решение: Воспользуемся 2-м замечательным пределом: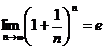

= .

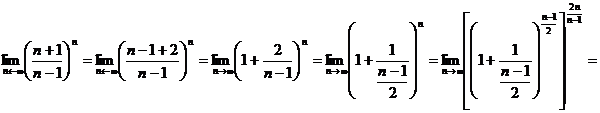
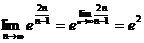Предел функции.

Опр.1.Число 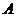называется пределом функци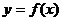и при 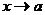, если для любой окрестности 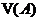числа 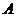существует такая проколотая окрестность 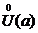числа a, что для всех ,

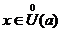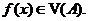
Это определение по Коши. Число 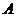может быть как конечным, так и бесконечным. В частности, если числа 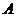и а конечны, получаем следующее определение (на языке “ - ”).

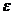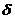Опр.2. Число 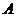называется пределом функци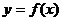и при 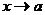, если для всякого 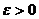существует такое число 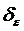>0, что для всех х, удовлетворяющих неравенству 0< 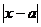< 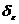и входящих в область определения функции 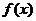, справедливо неравенство:

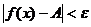(1)

и обозначается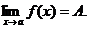

Если а = + 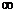, то получаем следующее определение.

Опр.3.Число 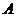называется пределом функци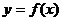и при 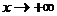, если для всякого 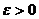существует такое число 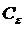>0, что для всех х, удовлетворяющих неравенству 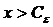и входящих в область определения функции 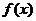, справедливо (1) и обозначается:

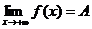(определение “ 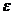-C”).

Определение предела функции по Гейне: Число А называется пределом функции y=f(x) при 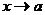(в точке a), если для любой сходящейся к числу а последовательности 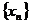значений х, входящих в область определения функции и отличных от a, соответствующая последовательность 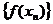этой функции сходится к числу А.

Пример 1. Пользуясь определением предела по Гейне, доказать, что

.

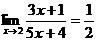Решение: Рассмотрим любую последовательность 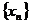, удовлетворяющую двум условиям:

1)

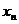
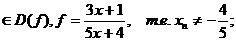
2) .

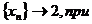
Этой последовательности 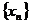соответствует последовательность значений функции:

…

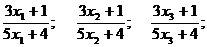Тогда на основании свойств сходящихся последовательностей (каких?) будем иметь

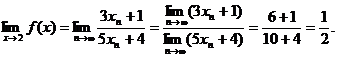
Т.о. независимо от выбора последовательности 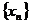, сходящейся к числу 2 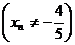, соответствующая последовательность значений функции 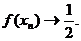А это на основании определения предела функции по Гейне значит, что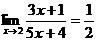

Замечание 1: Определением предела по Гейне удобно пользоваться тогда, когда доказывается, что функция f(x) не имеет предела. Для этого достаточно показать, что существует две последовательности но соответствующие последовательности 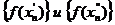имеют неравные пределы.

Пример 2: Доказать, что 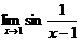не существует.

Решение: возьмем

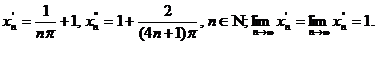
Тогда соответствующие последовательности значений функции таковы:

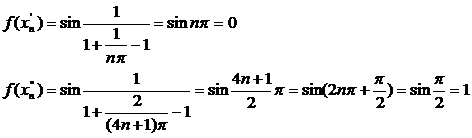
Следовательно,

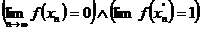, т.е. 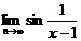не существует

Замечание 2: Пример 2 показывает, что вывод о наличии предела функции нельзя делать, исходя из последовательности {x_n} частного вида (например, исходя из x_n^'' =1+ 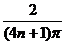), а нужно рассматривать произвольную последовательность {x_n }, имеющую заданный

предел а.

Пример 3: Пользуясь " 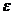– 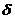" определением предела, доказать, что

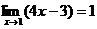
Решение: Надо доказать, что для "e>0 существует такое d_e >0, что из неравенства 0 < |x-1| < d_e следует, что |f(x)-1| < e, f(x)=4x-3. Зададим

e > 0 и рассмотрим выражение: |f (x)-1|=|4x-3-1|= 4|x-1|.

Если взять d_e ≤ e/4, то для всех х, удовлетворяющих неравенству |x-1| < d_e, будем иметь |f(x)-1| = 4|x-1|<4d_e ≤ 4e/4=e.

Следовательно,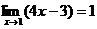

Пример 4: f(x)=1/(x-1) доказать, что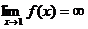

Решение: По определению 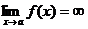, если для " М>0 можно подобрать d_М>0, что для всех х¹а, удовлетворяющих неравенству

0<|x-a|<d, будет выполняться условие 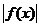>M. В нашем случае по заданному M>0 будем подбирать d_М из условия

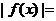| 1/|x-1|>M Ú |x-1|<1/M.

Следовательно, положив d_M=1/М, получим, что для всех х, удовлетворяющих неравенству 0<|x-1|<d_M, выполняется неравенство 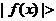M, значит,

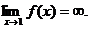
Вычисление предела функции.

При вычислении предела функции необходимо знать следующие

теоремы:

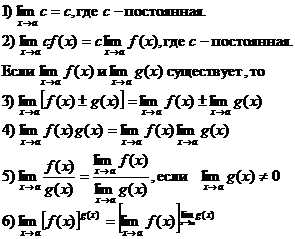
Кроме того, надо пользоваться тем, что для всех основных элементарных функций в любой точке их области определения справедливо равенство:

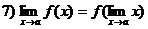(в силу непрерывности, Л.р. №7)

Этими простейшими пределами можно пользоваться как формулами:

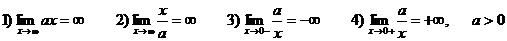
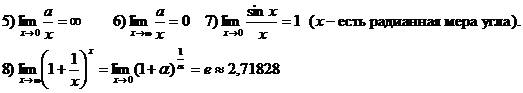
Более сложные случаи нахождения предела функции: 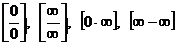,[1^¥] рассматриваются далее в отдельности.

Пример 1.Найти предел:

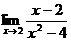
Решение:

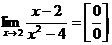
Разлагаем знаменатель на множители:

Здесь нет сокращения на нуль, что никогда недопустимо. Согласно определению предела функции аргумент х стремиться к своему предельному значению 2, никогда с ним не совпадая.

Пример 2. Найти предел:

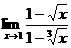
Решение:

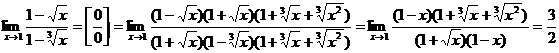Пример 3. Найти предел:

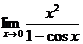
Решение:

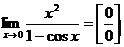
(Применяем тригонометрическую формулу так, чтобы использовать первый замечательный предел).

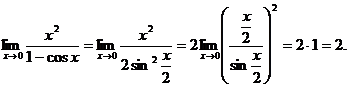
Пример 4. Найти предел:

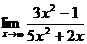
Решение:

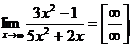
Деля числитель и знаменатель на наивысшую степень х (на х²), находим

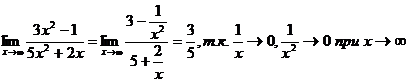
Случай, когда при х®а или х®¥ функция f(x) представляет произведение бесконечно малой величины на бесконечно большую 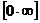, приводится путем преобразования функции к одному из двух рассмотренных случаев, т.е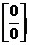. к или к .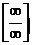

Случай, когда при х®а или х®¥ функция f(x) представляет разность двух положительных бесконечно больших величин 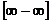, можно привести к случаю 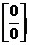или 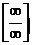путем преобразования функции к дроби.

Пример 5. Найти следующий предел:

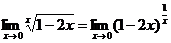
Решение:

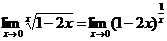
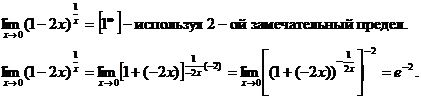
Непрерывность и точки разрыва функции.

Если ищется предел функции 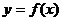при условии, что аргумент 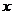, стремясь к своему предельному значению а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним (левым) пределом данной функции в точке 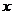=а и условно обозначается так:

=

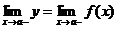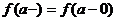
Аналогично можно сформулировать определение правостороннего (правого) предела данной функции, который обозначается так: