Определение площади. Площадь криволинейной трапеции. Площадь в полярных координатах.
Определение: Пусть множество  и A – ограничено. Рассмотрим множество
и A – ограничено. Рассмотрим множество 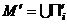 (объединение прямоугольников), такое что
(объединение прямоугольников), такое что  , и множество
, и множество  , такое что
, такое что 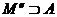 , и назовем
, и назовем  и
и 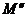 фигурами. Площади этих фигур
фигурами. Площади этих фигур  и
и  можно посчитать. Т.к. множество
можно посчитать. Т.к. множество  оганичено сверху (S(A))
оганичено сверху (S(A)) 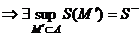 . Аналогично
. Аналогично  ограничено снизу (нулем)
ограничено снизу (нулем) 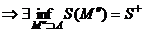 . Если
. Если 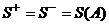 , то это площадь A, а множество называется квадрируемым.
, то это площадь A, а множество называется квадрируемым.
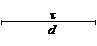 Пример1: Пусть τ – отрезок и
Пример1: Пусть τ – отрезок и  .
.  Ø. При этом S(M΄)=0 и
Ø. При этом S(M΄)=0 и 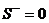 . Пусть длина отрезка равна d, тогда
. Пусть длина отрезка равна d, тогда 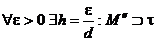 , а
, а 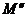 длины d и высоты h. Тогда
длины d и высоты h. Тогда 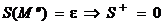 . Получили S(τ)=0.
. Получили S(τ)=0.
 Пример2:
Пример2: 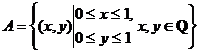 .
.  ,
,  Ø и
Ø и 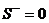 , т.к. никакой прямоугольник полностью не лежит в этом множестве.
, т.к. никакой прямоугольник полностью не лежит в этом множестве. 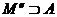 , т.е.
, т.е. 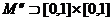 , поэтому
, поэтому  . Получаем, что
. Получаем, что  , поэтому множество A - не квадрируемое.
, поэтому множество A - не квадрируемое.
Пусть f(x)≥0 на [a,b]. Криволинейная трапеция T - множество (x,y), такое что a≤x≤b и 0≤y≤f(x).
Теорема: (О площади криволинейной трапеции).
Пусть функция f(x)≥0 на [a,b]. Криволинейная трапеция T квадрируема тогда и только тогда(Û), когда функция f(x) интегрируема на [a,b]. При этом площадь T равна: 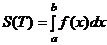 .
.

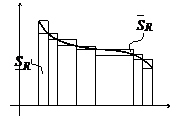 Доказательство: Ü: По основной теореме
Доказательство: Ü: По основной теореме 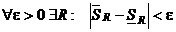 . Найдутся такие
. Найдутся такие  и
и 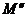 , что
, что 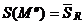 и
и 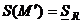 . Тогда
. Тогда  .
.
Þ: 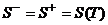 , так как криволинейная трапеция T квадрируема. Тогда
, так как криволинейная трапеция T квадрируема. Тогда 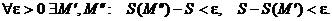
 Обе интегральные суммы стремятся к одному и тому же числу (S).
Обе интегральные суммы стремятся к одному и тому же числу (S). 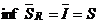 ,
,  . Следовательно
. Следовательно 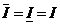 , поэтому функция f(x) интегрируема (из следствия основной теоремы).
, поэтому функция f(x) интегрируема (из следствия основной теоремы).
Пример. x2+y2=R2. a≤x≤b (a=-R, b=R), и 0≤y≤  . При этом
. При этом 
Замечание к определению площади: Множества  можно заменить на любые другие квадрируемые множества. Если
можно заменить на любые другие квадрируемые множества. Если 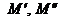 - фигуры,
- фигуры, 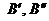 - квадрируемые множества, т.е. существуют площади
- квадрируемые множества, т.е. существуют площади 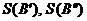 и при этом
и при этом 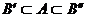 , то при
, то при 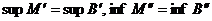 получим все то же самое.
получим все то же самое.

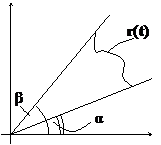 Пусть множество задано в полярных координатах: x=r·cost, y=r·sint. Рассмотрим множество A, такое, что α≤t≤β и 0≤r≤r(t). Введем разбиение угла [α,β]: α=t0<t1<t2<…<tn=β. При этом Δti=[ti ,ti+1]. Рассмотрим сектора окружностей ri=mi – это будут сектора
Пусть множество задано в полярных координатах: x=r·cost, y=r·sint. Рассмотрим множество A, такое, что α≤t≤β и 0≤r≤r(t). Введем разбиение угла [α,β]: α=t0<t1<t2<…<tn=β. При этом Δti=[ti ,ti+1]. Рассмотрим сектора окружностей ri=mi – это будут сектора  и ri=Mi – это будут сектора
и ri=Mi – это будут сектора 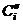 .
.  и
и  . Окружности (с углом 2π) соответствует площадь πR2, а сектору с углом α – площадь αR2/2. Поэтому
. Окружности (с углом 2π) соответствует площадь πR2, а сектору с углом α – площадь αR2/2. Поэтому  и
и 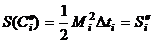 .
.  и
и  - нижняя и верхняя суммы Дарбý для функции f=r2/2. Получим
- нижняя и верхняя суммы Дарбý для функции f=r2/2. Получим 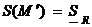 и
и 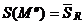 . То есть площадь S(A) существует и равна S (т.е. A квадрируема) тогда и только тогда, когда существует интеграл
. То есть площадь S(A) существует и равна S (т.е. A квадрируема) тогда и только тогда, когда существует интеграл  .
.
Билет 49
Определение объёма. Объем тела вращения.
 .Тогда пусть
.Тогда пусть  ,
, 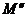 фигуры, которые удовлетворяют условию:
фигуры, которые удовлетворяют условию:  ;
;  .
.
Тогда внешний объем равен:  , а внутренний:
, а внутренний:  .
.
Если 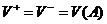 , то множество
, то множество  - кубируемое.
- кубируемое.
Лемма:(объем цилиндра)
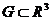 - множество точек плоскости, удовлетворяющих условию
- множество точек плоскости, удовлетворяющих условию 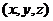
 и
и  , то
, то 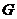 - цилиндр. Его объем равен:
- цилиндр. Его объем равен: 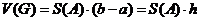 . Так как
. Так как  - квадрируемое множество, то:
- квадрируемое множество, то:  . Значит
. Значит 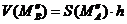 ;
;
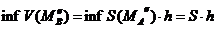 , соответственно
, соответственно  . Значит объем цилиндра равен
. Значит объем цилиндра равен 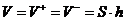 .
.


Теперь непосредственно рассмотрим вращение произвольное тело вращения.
Пусть 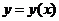 - есть произвольная непрерывная функция, причем
- есть произвольная непрерывная функция, причем  на отрезке
на отрезке 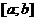 . Будем вращать данную кривую на отрезке
. Будем вращать данную кривую на отрезке 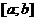 вокруг оси
вокруг оси 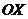 . Получим тело вращения
. Получим тело вращения 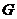 .
.
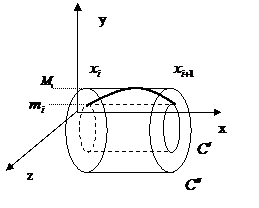
Разобьем отрезок 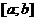 :
:  . Пусть
. Пусть 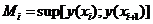 ,
, 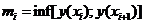 . Рассмотрим два цилиндра
. Рассмотрим два цилиндра 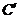 и
и  (см. рис. )
(см. рис. ) 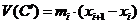 ,
, 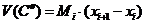 . Теперь пусть
. Теперь пусть
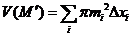 и
и  . Нетрудно видеть , что
. Нетрудно видеть , что
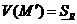 и
и  . Это означает, что если функция
. Это означает, что если функция  интегрируема на отрезке
интегрируема на отрезке 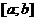 , то
, то  и
и  . При вращении вокруг оси
. При вращении вокруг оси  формула примет вид
формула примет вид  .
.
Пример:Рассмотрим вычисление объема тела вращения на примере шара:
 . Значит объем шара равен:
. Значит объем шара равен:  .
.
Билет 50
