Формула Тейлора для дифференцируемых функций.
Если функция f(x) n раз дифференцируема в точке а, то для нее существует многочлен 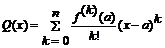 - это многочлен Тейлора n-го порядка функции f(x) в точке a. Обозначим за
- это многочлен Тейлора n-го порядка функции f(x) в точке a. Обозначим за 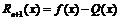 - на сколько многочлен отличается от самой функции.
- на сколько многочлен отличается от самой функции. 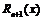 называют остаточным членом. Нужно доказать, что для «хороших» функций
называют остаточным членом. Нужно доказать, что для «хороших» функций 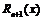 будет достаточно мало. Докажем теорему, которую сформулируем в конце. =))
будет достаточно мало. Докажем теорему, которую сформулируем в конце. =))
Рассмотрим функцию f; зафиксируем точку a, в которой будем раскладывать функцию, и произвольную точку x, такую что f(x) n-1 раз дифференцируема на [a,x] и n раз дифференцируема на (a,x). В точке а функция дифференцируема n-1 раз, значит для нее можно составить многочлен Тейлора n-1 порядка.
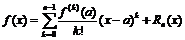
Представим 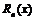 в виде:
в виде: 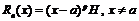 , где р – произвольное число, H – некоторая функция, зависящая от x.
, где р – произвольное число, H – некоторая функция, зависящая от x.
Рассмотрим функцию : 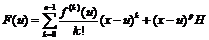
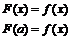
Рассмотрим F(u) на [a,x]: F(u) непрерывная на [a,x], дифференцируема на (a,x), F(x)=F(a) 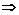 по теореме Ролля
по теореме Ролля 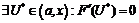
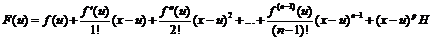 ; продифференцируем:
; продифференцируем:






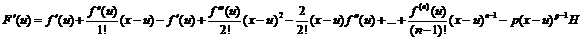 - и почти все взаимно уничтожается.
- и почти все взаимно уничтожается.
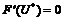
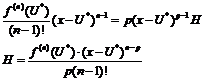
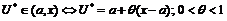 , тогда
, тогда 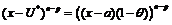
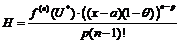 ;
; 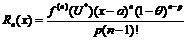 Подставим теперь p:=n;
Подставим теперь p:=n;
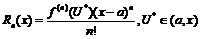 - это остаточный член в форме Лагранжа. Подставим теперь p:=1
- это остаточный член в форме Лагранжа. Подставим теперь p:=1
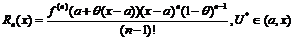 - это остаточный член в форме Коши.
- это остаточный член в форме Коши.
Рассмотрим форму Лагранжа:
Пусть теперь f имеет непрерывную n-ю производную в точке а. Это означает, что на [a,x) функция n раз дифференцируема. Значит f(x) можно представить в виде:
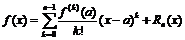 ;
; 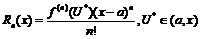
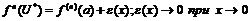 , т.к. производная непрерывна. Тогда
, т.к. производная непрерывна. Тогда 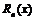 можно представить в виде:
можно представить в виде:
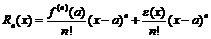 ;
; 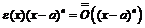
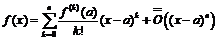 - это формула Тейлора с остаточным членом в форме Пеано.
- это формула Тейлора с остаточным членом в форме Пеано.
Таким образом, мы доказали следующую теорему:
Теорема
Если функция n-1 раз дифференцируема на [a,x], n раз на (a,x), то она раскладывается по формуле Тейлора с остаточными членами в форме Лагранжа и Коши. Если функция f(x) имеет непрерывную n-ю производную в точке а, то в окрестности точки а она раскладывается по формуле Тейлора с остаточными членами в форме Лагранжа, Коши и Пеано.
Теорема (о единственности разложения функции по формуле Тейлора в форме Пеано)
Если 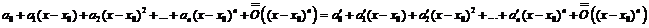 , то
, то 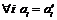 ,
, 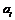 - коэффициенты из формулы Тейлора. Т.е. если есть какие-то другие коэффициенты
- коэффициенты из формулы Тейлора. Т.е. если есть какие-то другие коэффициенты 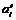 , то они тоже есть коэффициенты из формулы Тейлора:
, то они тоже есть коэффициенты из формулы Тейлора: 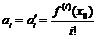
Доказательство.
Устремим 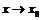 , получим, что
, получим, что 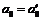 , т.к.
, т.к. 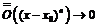 ; тогда
; тогда
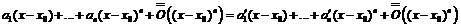
сократив на 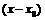 , получим:
, получим:
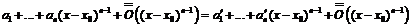 и опять же
и опять же 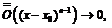 если
если 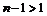 .
.
И так мы можем проделать до n-го коэффициента. Теорема доказана.
Билет 19
Формула Тейлора для важнейших элементарных функций.
Общий вид формулы Тейлора для функций:
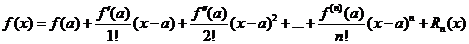 , где
, где 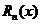 - остаточный член.
- остаточный член.
При 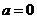 получаем так называемую формулу Маклорена.
получаем так называемую формулу Маклорена.
Формула Тейлора для важнейших элементарных функций:
1) 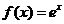 ,
,
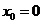 ,
, 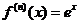 ,
, 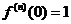 . Отсюда получаем, что
. Отсюда получаем, что
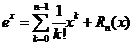 .
. 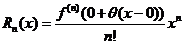 ,
,
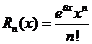 , где
, где 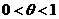 . И в итоге имеем:
. И в итоге имеем: 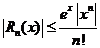 ,
, 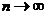 ,
, 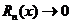 .
.
Пример:
Пусть 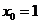 , тогда получим:
, тогда получим:
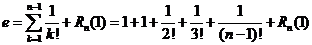 ,
, 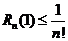 .
.
2) 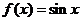 ,
,
Поскольку  ,
, 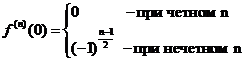 , формула имеет вид:
, формула имеет вид: 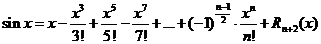 , где n – нечётное число, а остаточный член в форме Лагранжа равен
, где n – нечётное число, а остаточный член в форме Лагранжа равен 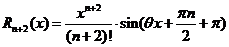 ,
, 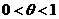 .
.
Очевидно, что для остаточного члена справедлива следующая оценка: 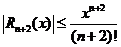 .
.
3) 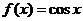 ,
,
Поскольку 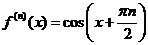 , то
, то
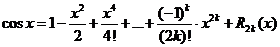 ,
, 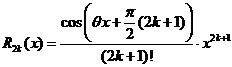 ,
,
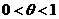 ,
, 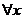
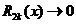 ,
, 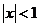 .
.
4) 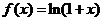 ,
,
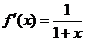 ,
, 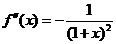 ,
, 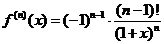 ,
, 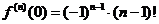 ,
,
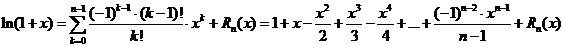 ,
,
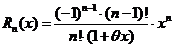 ,
, 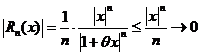 при
при 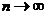 ,
,
Рассмотрим остаточный член в форме Коши:
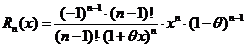 ,
, 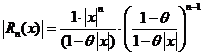 ,
, 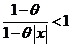 ,
,
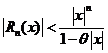 , где
, где 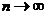 ,
, 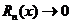 и
и 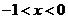 .
.
5) 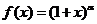 ,
,
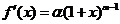 ,
, 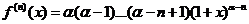 ,
, 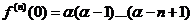 ,
,
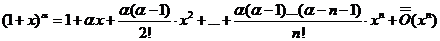 ,
,
Остаточный член в форме Пеано.
Билет 20
