Производные высших порядков. Формула Лейбница.

Пусть функция y=f(x) дифференцируема в точке Xo, то есть существует ее производная в этой точке f ’ (Xo). Пусть f - дифференцируема в некоторой окрестности U(Xo). f’(x) определена на U(Xo) и если дифференцируема в точке Xo, то (f’(Xo))’=f’’(Xo). Вообще

Теорема: (Формула Лейбница)

Пусть функции U и V n раз дифференцируемы, т.е. существуют 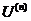и . Значит (U*V) – тоже n раз дифференцируема, при этом

Доказательство:

Метод математической индукции:

Пусть при n=m – верно, т.е.

(*)

Надо доказать, что

Доказательство:

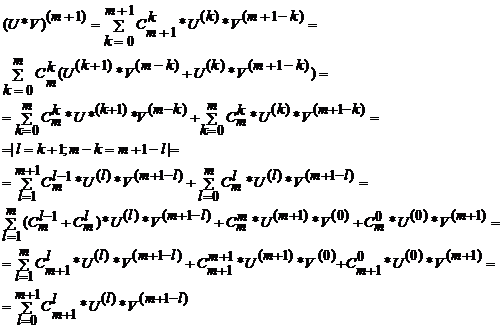
Теорема доказана.

Билет 10

Дифференциалы высших порядков. Инвариантность формы первого дифференциала. Неинвариантность формы дифференциалов второго и высших порядков.

f(x) дифференцируема,

тогда . Далее, пусть f – n раз дифференцируема,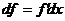

__________________________

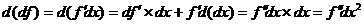
. Докажем, что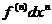

1) ,

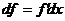
2) Пусть при n = m

3)

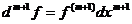
Инвариантность/Неинвариантность.

1) y(x), x – независимая переменная, , пусть x = x(t)

2) y(x), x – независимая переменная, , ,

, здесь , .

Билет 11

Возрастание (убывание) функции в точке. Необходимое и достаточное условие. Теорема Ферма.

Определение 1:. f(x) – возрастает (не убывает) в точке 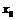, если

.

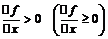Определение 1’. f(x) – возрастает (не убывает) в точке 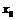, если

Определение 1’’. f(x) – возрастает (не убывает) в точке 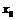, если

Определение 2. f(x) – убывает (не возрастает) в точке 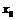, если

.

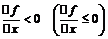Определение 2’. f(x) – убывает (не возрастает) в точке 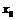, если

Определение 2’’. f(x) – убывает (не возрастает) в точке 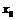, если

Теорема 1:(Необходимое условие возрастания (неубывания) функции в точке )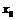

Если f возрастает (не убывает) в точке 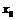и дифференцируема в точке 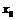, то .

Доказательство:

Т.к. функция возрастает (не убывает), то, по определению 1’’ ,

, а значит и . Теорема доказана.

Теорема 1’(Необходимое условие убывания (невозрастания) функции в точке )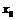

Если f убывает (не возрастает) в точке 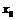и дифференцируема в точке, то .

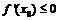Доказательство:

Т.к. функция убывает (не возрастает), то, по определению 2’’ ,

, а значит и , теорема доказана.

Теорема 2: (Достаточное условие возрастания)

Если f(x) дифференцируема в точке 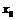, причем , то f(x) возрастает в точке .

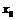Доказательство:

По теореме о сохранении знака:

, значит

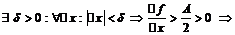f возрастает.

Теорема доказана.

Замечание: если , то про возрастание сказать ничего нельзя.

Теорема 2’: (Достаточное условие убывания)

Если f(x) дифференцируема в точке 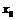, причем 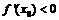, то f(x) убывает в точке .

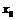Доказательство:

По теореме о сохранении знака:

, значит

f(x) убывает.

Теорема доказана.

Замечание: если 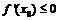, то про убывание сказать ничего нельзя.

Теорема Ферма:(Необходимое условие существования экстремума)

Если f(x) дифференцируема в точке 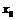и 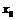– точка локального экстремума, то .

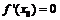Доказательство:

Пусть f(x) возрастает в точке 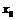, т.е.

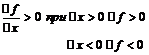, т.е. 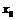– не точка экстремума.

Аналогично невозможен случай 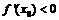, следовательно .

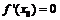Теорема доказана.

Билет 12

Теорема Ролля.

Теорема:

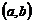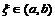Если функция непрерывна на , дифференцируема на и , то существует точка , такая, что .

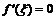Доказательство:

Так как функция f непрерывна на [a,b], то существует точка x₁, в которой f достигает максимума и точка x₂, в которой f достигает минимума. Рассмотрим 2 случая:

1. Обе точки x₁ и x₂ совпадают с a или b, тогда

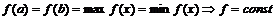
И тогда производная

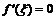
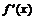1. Одна из точек не является концевой отрезка [a,b]. Пусть - та из них, которая , тогда в точке достигается локальный экстремум, кроме того, , так как по условию существует . Поэтому по теореме Ферма 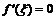, что и требовалось доказать.

Контрпример 1

Уберем непрерывность в точке b: теорема потеряет силу.

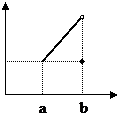
Контрпример 2

Уберем дифференцируемость в одной из точек: теорема потеряет силу.

Теорема Ролля имеет простой геометрический смысл: если выполнены все условия теоремы, то на графике функции ! существует точка касательная в которой параллельна оси x.

Физический смысл: при прямолинейном движении если перемещение тела = 0, то существует момент времени, в который скорость тела = 0.

Билет 13