Практическая работа 4 «Действия с комплексными числами в алгебраической и тригонометрической формах»
Цель: формировать умения по решению основных типов задач
Задание 1. Даны комплексные числа в алгебраической форме. НайтиZ1- Z2 ; Z1×Z2
1.  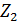 = = 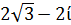 2. 2.  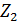 = =  3. 3. 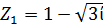 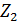 = = 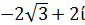 4. 4. 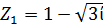 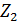 = =  |
Задание 2. Перевести комплексные числа Z1 и Z2 в тригонометрическую форму.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем состояла потребность появления комплексных чисел?
2. Что называется комплексным числом?
3. Когда два комплексных числа называются равными?
4. Что называется
а) суммой комплексных чисел,
б) противоположным числом,
в) комплексным нулем,
г) разностью комплексных чисел,
д) произведением комплексных чисел,
е) частным от деления комплексных чисел?
5. Назовите свойства операции сложения комплексных чисел.
6. Что такое мнимая единица?
7. Как выглядит комплексное число в
а) алгебраической форме
б) тригонометрической форме
8. Как выглядит арифметические операции сложения, вычитания, деления и умножение комплексных чисел, записанных в алгебраической форме?
9. Как представить комплексное число геометрически?
10. Что такое модуль комплексного числа и как его вычислить?
11. Что такое аргумент?
12. Как перейти от алгебраической формы записи комплексного
числа к тригонометрической?
Линейная алгебра
Матрицы и операции над ними
Основные понятия
Определение. Прямоугольная таблица
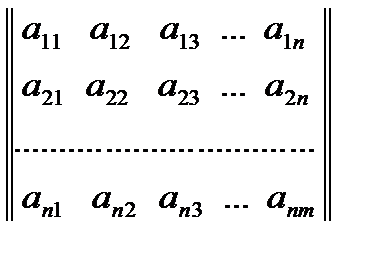 , ( 1 )
, ( 1 )
составленная из n∙m чисел, называется матрицей из n строк и m столбцов или матрицей размера n x m, а также n x m – матрицей.
Числа  (i = 1, 2,…,n; j = 1, 2, …,m) называются элементами матрицы; первый индекс i элемента указывает номер строки, в которой стоит элемент матрицы, а второй индекс j – номер столбца.
(i = 1, 2,…,n; j = 1, 2, …,m) называются элементами матрицы; первый индекс i элемента указывает номер строки, в которой стоит элемент матрицы, а второй индекс j – номер столбца.
Матрица (1) может обозначаться также 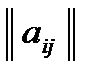 , i = 1, 2,…n, j = 1, 2,…m.
, i = 1, 2,…n, j = 1, 2,…m.
Кроме того, для матриц используются обозначения
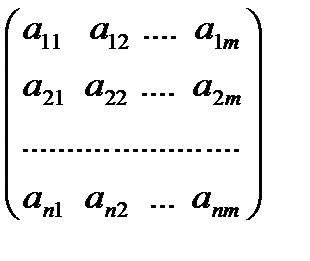 или
или 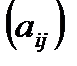 ;
;  или
или 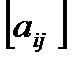 .
.
Например,  .
.
Если число строк матрицы равно числу столбцов (и равно n), то матрица называется квадратной порядка n, например,  – матрица порядка 3.
– матрица порядка 3.
Две матрицы 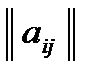 и
и 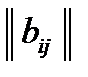 называются равными, если числа их строк и столбцов соответственно равны и равны числа, стоящие на соответственных местах: aij = bij при i = k и j = l.
называются равными, если числа их строк и столбцов соответственно равны и равны числа, стоящие на соответственных местах: aij = bij при i = k и j = l.
Элементы a11, a22 ,…,ann квадратной матрицы порядка n называются диагональными элементами.
Квадратная матрица, все диагональные элементы которой равны 1, а остальные – нули, называется единичной и обозначается Е или Еn.
Например,
Е = 
Для любой квадратной матрицы порядка n справедливо равенство: En ∙A = A∙En = A.
Матрица вида 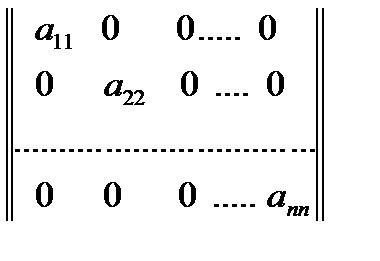 , где все элементы кроме диагональных, равны нулю, называется диагональной. Элементы а11, а22, …, аnn образуют главную диагональ.
, где все элементы кроме диагональных, равны нулю, называется диагональной. Элементы а11, а22, …, аnn образуют главную диагональ.
Например, 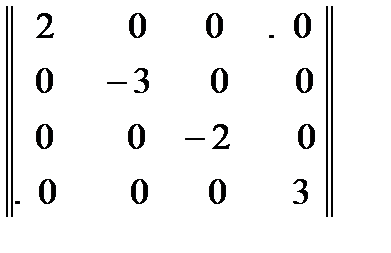 ,
,
где 2, -3, -2, 3 – главная диагональ.
Матрица, получаемая путем замены строк на столбцы, а столбцов на строки, называется транспонированной относительно данной.
Например,
 и
и  - транспонированные матрицы.
- транспонированные матрицы.
Операции над матрицами
Суммойдвух матриц одинакового размера А + В, где А = 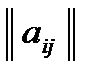 , В =
, В = 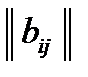 есть матрица С =
есть матрица С =  того же размера с элементами сij = aij + bij при всех i и j. Т.е. сложение матриц одинакового размера производится поэлементно.
того же размера с элементами сij = aij + bij при всех i и j. Т.е. сложение матриц одинакового размера производится поэлементно.
Например,
Найти сумму матриц А + В, если
A =  , B =
, B =  .
.
С =  =
= 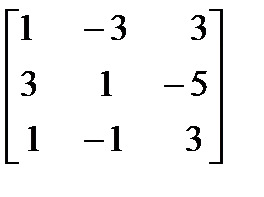 .
.
Произведениемматрицы на действительное число называется матрица, элементы которой получены умножением на это число всех элементов данной матрицы: λА = λ 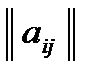 , где λ – число.
, где λ – число.
Например,
2  =
=  .
.
Произведениемматриц А и В, (причем число столбцов первой матрицы равно числу строк второй матрицы), называется матрица С, элементы которой равны сумме произведений элементов каждой строки матрицы А на каждый элемент столбца матрицы В.
Т. е. сij = ai1b1j + ai2b2j +…+ a1nbnj , i = 1, 2,…, m; j = 1, 2,…, k.
Например,
С = А ∙ В = 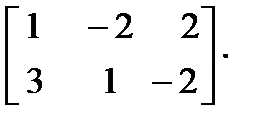
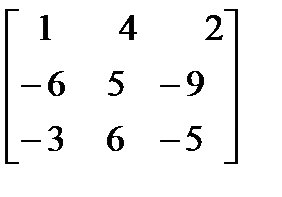 =
=  , где
, где
с11 = 1∙1 + (-2) ∙ (-6) + 2 ∙ (-3) = 7
с21 = 3 ∙1 + 1 ∙ (-6) + (-2) ∙ (-3) = 3
с12 = 1∙ 4 + (-2) ∙ 5 + 2 ∙6 = 6
с22 = 3 ∙ 4 + 1 ∙ 5 + (-2) ∙ 6 = 5
с13 = 1∙ 2 + (-2) ∙ (-9) + 2 ∙ (-5) = 10
с23 = 3 ∙ 2 + 1 ∙ (-9) + (-2) ∙ (-5) = 7.
Определители и их свойства
Определение 1. Таблица вида 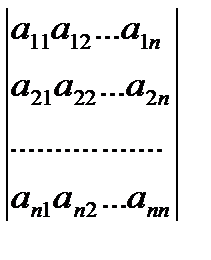 , где a11, a12,…a1n,…an1,…ann – некоторые числа, называется определителем матрицы порядка n.
, где a11, a12,…a1n,…an1,…ann – некоторые числа, называется определителем матрицы порядка n.
Например: 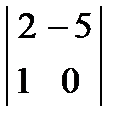 ,
, 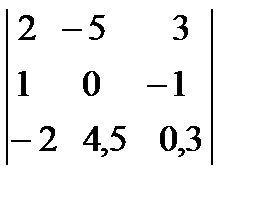 - определители 2 – го и 3 – го порядков.
- определители 2 – го и 3 – го порядков.
Вычисление определителя осуществляется по определенному правилу:
1) создать сумму произведений элементов по одному из каждой строки и каждого столбца со знаком + или – ;

– +

+ -
=  ;
;
Например:
1) Вычислить определитель 2 – го порядка:  .
.
Для этого удобно пользоваться правилом 1: 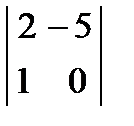 =
= 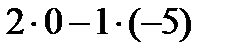 =5
=5
2) Вычислить определитель 3-его порядка:  .
.
Получим:
 =
= 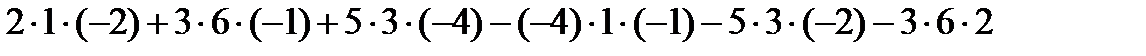 = – 92.
= – 92.
