Основные свойства неопределённого интеграла

№	Задания	Ответы

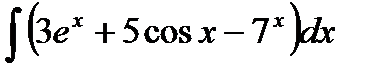Интегрирование подстановкой

№	Примеры	Ответы
1.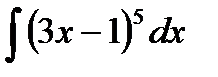
2.
3.
4.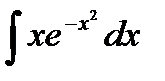
5.

Вычисление определённого интеграла

Вычислить:	Ответы:
1. 2. 3. 4.

Контрольные вопросы

1. Дать определение первообразной функции

2. Что называют неопределенным интегралом?

3. Перечислите свойства неопределенного интеграла.

4. Назовите действие, обратное к дифференцированию.

5. Как проверить правильность вычисления интеграла?

6. При интегрировании методом подстановки придерживаются следующего порядка:

А) интегрировать

Б) подставить в интеграл новые переменные

В) выразить дифференциал

Г) вычислить дифференциал

Д) заменить переменную

Е) выполнить обратную замену переменных.

Элементы комбинаторики

Теоретический материал

Определение 1. Размещения – это комбинации, составленные из n элементов по m элементов, которые отличаются друг от друга элементами и порядком элементов, и обозначаются .

Определение 2. Сочетания – это комбинации, составленные из n элементов по m элементов, которые отличаются друг от друга только элементами, и обозначаются .

Определение 3. Перестановки – это комбинации, составленные из n элементов по n элементов, которые отличаются друг от друга только порядком элементов, и обозначаются .

Формулы расчета комбинаций

= = ; = ;Pn = n! = 1∙2∙…∙ n

= ;

P_n = n! = 1∙2∙…∙ n

Замечание. 1) Т.к. n! = 1 ∙ 2 ∙ 3 ∙ …∙ n, то

1)При работе с факториалами важно понимать, что в большем факториале можно выделить меньший и домножить на такое количество увеличивающихся на 1 ед. множителей пока ни достигнем значения данного факториала.

Например,10! = 7!∙8∙9∙10; 10!= 5!∙6∙7∙8∙9∙10.

2)Использовать действия умножения, сложения, вычитания и т.д. только после того как упростятся выражения.

Примеры решения задач по комбинаторике

Вычислить: 1) .

Решение:

= 8∙7∙6∙5–8∙7∙6=8∙7∙6(5–1)=56∙24 =1344

2) Сократить дробь: .

Решение: =

3) Вычислить: .

Решение:

Используем формулу

= = =

Сократим 3!

=

представим 4! =2!∙3∙4, 7!=5!∙6∙7

окончательно после сокращения 2! и 5!

= =

Решить задачи

а)На тренировках занимаются 12 баскетболистов. Сколько может быть образовано тренером разных спортивных пятерок?

Решение. Т. к. пятерки отличаются друг от друга хотя бы одним игроком, то их возможное количество определяется сочетаниями

= = 792.

b)В высшей лиге по футболу 18 команд. Борьба идет за золотые, серебренные и бронзовые медали. Сколькими способами могут быть распределены медали между командами?

Решение. Т. к. в задаче важно знать, сколько троек команд нужно рассмотреть и порядок завоеванных ими мест имеет значение, то мы имеем дело с размещениями

= 18 ∙ 17 ∙ 16 = 4896.

c) Сколько четырехзначных чисел можно записать при помощи цифр 1, 2, 3, 4, если каждая из них входит в изображение числа только один раз.

Решение. Т.к. число состоит из всех четырех цифр, то одно от другого их отличает только порядок между цифрами, т. е. имеет место перестановка без повторений:

Р₄ (1,1,1,1) = 4! = 1 ∙ 2 ∙ 3 ∙ 4 = 24.

d)Для подготовки праздника выбирают комиссию в составе 3 девушек и 4 юношей. Сколькими способами это можно сделать, если в группе 14 девушек и 18 юношей?

Решение. Рассмотрим отдельно, сколько троек из 14 девушек можно организовать для комиссии. Т.к. они различные, то это сочетания . Аналогично узнаем, сколько различных четверок можно составить из 18 юношей: . Каждая из троек девушек образует по столько комиссий, сколько четверок имеем из юношей, т.е. общее количество комиссий равно:

∙ = 1113840.

Основные понятия теории вероятностей

Виды случайных событий

Событие называется случайным, если оно может произойти, а может не произойти.

Событие называется достоверным, если оно произойдет при любом количестве испытаний.

Событие называется невозможным, если оно никогда не произойдет.

События называются несовместными, если вместе они произойти не могут.

Два события называются противоположными, если одно из них происходит в том и только в том случае, когда не происходит другое. Обозначаются: А, . (А – упал, - не упал).

События А₁, А₂, …, А_n образуют полную группу событий, если в результате данного испытания произойдет хотя бы одно из них. (А – игра. Исходы: А₁ – выигрыш, А₂ – проигрыш, А₃ – ничья). Иными словами: все варианты одного и того же события образуют полную группу событий.

События А и В называются равновеликими, если событие А происходит тогда и только тогда, когда происходит событие В и наоборот.

Определение 1. Вероятностью р события А называется отношение числа исходов, благоприятствующих наступлению данного события, к числу всех исходов данного события. Обозначается Р(А) или просто р.

Р(А) =

где n – общее количество исходов данного события А

m – количество благоприятных исходов события А.

Т.к. количество благоприятных исходов для достоверного события U равно общему количеству, а количество благоприятных исходов для невозможного события V равна нулю, то

Р(V) =

Р(U) =

Отсюда следует:

0 < P < 1

Следствие.Сумма вероятностей событий, образующих полную группу, равна 1.

Например.

А – игра в шахматы.

Исходы: А₁ – выигрыш, Р(А₁) =0,45; А₂ – проигрыш, Р(А₂) = 0,3; А₃ – ничья, Р(А₃) = 0,25.

Р(А₁) + Р(А₂) + Р(А₃) = 0,45+0,3+0,25=1.

Примеры

1) Бросается игральный кубик. Какова вероятность, что выпадет 3 очка (событие А)?

Решение. Общее количество возможных исходов–6 (количество граней кубика). Число благоприятных исходов – 1 (количество граней с тремя очками).

Отв. 1/6.

2)В урне находится 3 синих, 8 красных и 9 белых шаров одинакового размера и веса. Наугад вынимается один шар. Какова вероятность того, что он а) синий, b) красный, c) белый.

Решение. Пусть вынули а) синий шар – событие С, b) красный шар – событие – К, с) белый шар – событие В.

Общее количество возможных исходов – 20 (общее количество шаров).

Благоприятных исходов для события С – три ( общее количество синих шаров), для события К – восемь (8 – красных шаров) и для события В – девять (9 белых шаров).

Отсюда по определению вероятности имеем:

Р(С) = 3/20, Р(К) = 8/20 = 2/5, Р(В) = 9/20.

3) Группа туристов из 10 человек (7 юношей и 3 девушки) выбирает четырех дежурных. Какова вероятность того, что все дежурные юноши?

Решение. Определим n – общее количество вариантов четверок дежурных – и m – количество вариантов четверок только из юношей – .

Тогда искомая вероятность Р = / = 1/6.

4) На отдельных карточках написаны буквы: а, р, к, у, ч. После перемешивания берут по одной карточке и кладут последовательно рядом. Найти вероятность того, что получится слово «ручка».

Решение. Число n – число возможных вариантов равно числу перестановок Р₅ = 5! Из всех этих вариантов только одна дает слово «ручка», т.е. m = 1.

Тогда Р(«ручка») = 1/5! = 1/120 = 0,008.

5) В партии из 10 деталей 7 стандартных. Найти вероятность того что среди шести наугад взятых деталей 4 стандартных.

Решение. Определим n – общее количество вариантов выбора шестерок из десяти деталей: .

Определим m – количество, благоприятствующих событию А (среди шести 4 стандартные) исходов. Четыре стандартные можно взять из семи стандартных деталей способами; при этом остальные 6–4=2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10–7=3 нестандартных деталей можно способами.Следовательно,число m – количество, благоприятствующих событию А исходов равно ∙ . Тогда искомая вероятность равна: Р(А) = ( ∙ ) / =½.

Математическая статистика

Выборка

Пусть требуется изучить некоторую совокупность объектов относительно некоторого признака. При этом или объектов много или исследование всех слишком дорого, или исследование ведет к уничтожению объектов.

Определение 1. Генеральной совокупностью называется множество числовых значений некоторого признака всех объектов данной совокупности.

Определение 2. Выборочной совокупностью иливыборкой называется множество числовых значений некоторого признака всех объектов, случайно отобранных из всей данной совокупности.

Например,партия всех лампочек – это генеральная совокупность. Множество лампочек, взятых для исследования – это выборочная совокупность.

Определение 3.Число объектов данной совокупности называется объемом.

Например,цех выпустил 2000 деталей, а для обследования взяли 150, то объем генеральной совокупности – N = 2000; объем выборочной совокупности – n = 150.

Основные виды выборок

Простой отбор – из генеральной совокупности случайно извлекается по одному объекту.

Например, белые медведи.

Типический отбор – объекты для выбора отбираются из каждой «типической» части совокупности. Например, детали отбираются для исследования пропорционально из каждого цеха.

Механический отбор –объекты отбираются через определенный интервал. Например, каждая 1, 5, 10, … деталь.

Серийный отбор – выборка целой серии объектов. Например, если условия работы в цехе не меняются в течение недели, то можно исследовать один день.