Найти математическое ожидание дискретной случайной величины, заданной законом распределения

A. 0,535;

B. 1,36;

C. 1;

D. 0,453.

Сравните величины σ для двух кривых НРС B

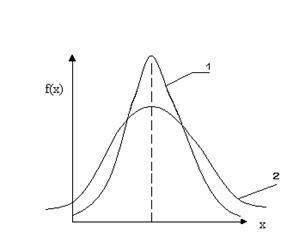A.

Непрерывная случайная величина Х задана плотностью распределения вероятностей . Тогда математическое ожидание этой нормально распределенной случайной величины равно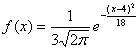

C. 4.

Для стандартизованного нормального распределения величина σ равна:

A. 1;

B. 2;

C.

Непрерывная случайная величина, возможные значения которой лежат в некоторых конечных пределах, распределена по закону равномерной плотности, если:

A. плотность вероятности постоянна;

B. все значения случайной величины имеют одинаковую вероятность;

C. плотность вероятности будет неотрицательной величиной и интеграл от плотности по отрезку, в котором заключены все значения случайной величины, равен единице.

Укажите условие нормировки непрерывной случайной величины:

A.

B.

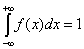C.

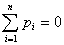D.

Вероятность появления какого-либо события из нескольких несовместных событий…

A. больше вероятности каждого отдельного события;

B. меньше вероятности каждого отдельного события;

C. равна вероятности каждого отдельного события;

D. равна вероятности наиболее вероятного события;

E. равна вероятности наименее вероятного события.

Укажите формулу для определения математического ожидания дискретной случайной величины:

A.

B.

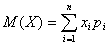C.

D.

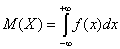Укажите формулу для определения математического ожидания непрерывной случайной величины:

A.

B.

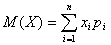C.

D.

Укажите формулу для определения дисперсии дискретной случайной величины:

A.

B.

C.

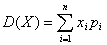D.

Функция распределения дискретной случайной величины…

A. показывает вероятность того, что случайная величина примет значения меньше величины , т.е

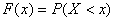B. показывает вероятность того, что случайная величина примет значения больше величины , т.е.

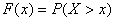C. равна вероятность того, что случайная величина примет значения , т.е.

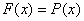D. показывает вероятность того, что случайная величина примет значения меньше либо равно величины , т.е.

Функция распределения дискретной случайной величины может быть представлена следующим образом:

A.

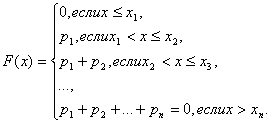B.

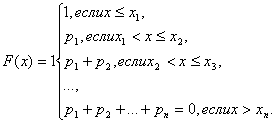C.

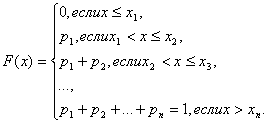D.

Укажите формулу для определения среднего квадратического отклонения случайной величины:

A.

B.

C.

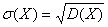D.

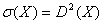Укажите правильные высказывания:

A. Относительной частотой случайного события А называется величина, равная пределу, к которому стремится отношение числа случаев, в которых реализуется событие А, к общему числу испытаний при неограниченном увеличении числа испытаний.

B. Относительной частотой случайного события А называется величина, равная отношению числа испытаний, в которых реализуется событие А, к общему числу испытаний.

C. Вероятность появления какого-либо события из нескольких несовместных событий больше вероятности каждого отдельного события.

D. Вероятность появления какого-либо события из нескольких несовместных событий равна произведению их вероятностей.

Укажите правильные высказывания:

A. Функция распределения непрерывной случайной величины указывает вероятность нахождения случайной величины в некотором интервале, отнесенную к ширине этого интервала.

B. Вероятность появления какого-либо события из нескольких несовместных событий меньше вероятности каждого отдельного события.

C. Плотность вероятности непрерывной случайной величины указывает вероятность того, что случайная величина принимает значения не больше х.

D. Функция распределения непрерывной случайной величины указывает вероятность того, что случайная величина принимает значения меньшие х.

Укажите правильные высказывания:

A. Плотность вероятности непрерывной случайной величины указывает вероятность нахождения случайной величины в некотором интервале, отнесенную к ширине этого интервала.

B. Площадь фигуры, ограниченной графиком функции плотности вероятности нормального закона распределения и осью абсцисс, равна 0,5.

C. Площадь фигуры, ограниченной графиком функции плотности вероятности нормального закона распределения и осью абсцисс, равна 1.

D. Математическое ожидание характеризует среднее значение случайной величины.

E. Дисперсия характеризует среднее значение случайной величины.

Укажите правильные высказывания:

A. Среднее квадратическое отклонение характеризует среднее значение случайной величины.

B. Математическое ожидание характеризует среднее значение случайной величины.

C. Дисперсия характеризует рассеяние случайной величины относительно ее математического ожидания.

D. Случайная величина называется непрерывной, если она принимает любые значения внутри некоторого интервала.

E. Случайная величина называется дискретной, если она принимает любое из значений в некотором интервале.

Укажите формулу плотности вероятности нормально распределенной непрерывной случайной – формулу Гаусса:

A.

B.

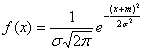C

Случайная величина Х распределена нормально m=1,σ=3 , Укажите функцию плотности распределения величины Х:

A.

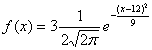B.

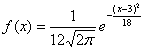C.

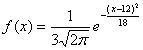D.