Последовательность действий.

1. Подготовьте таблицу, как показано на рис.7.

2. В ячейку Е3 введите значение ε.

3. Используя автозаполнение введите номер итерации n в столбце А.

4. В ячейку В7 введите значение x₀, т.е. запишите формулу: В7=D2.

5. В ячейки C7, D7, E7 введите формулы для вычисления значений функции y=f(x), ее производной и абсолютной величины функции 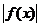соответственно:

C7=B7*Ln(B7)-1, D7=Ln(B7)+1, E7=ABS(C7)

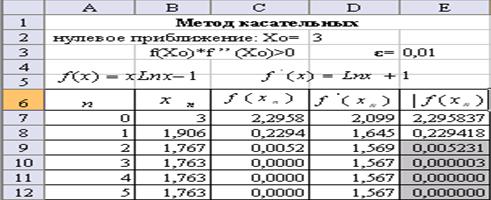
Рис.7.

6. В ячейку B8 введите формулу (5.3) для вычисления 1-го приближения: B8=B7-C7/D7.

7. Скопируйте ячейки C7, D7, E7 на строку ниже, т.е. соответственно в C8, D8, E8 и вы получите значения функции, ее производной и значение абсолютной величины функции в точке первого приближения х₁ .

8. Выделите блок ячеек В8:Е8 и скопируйте их вниз до конца таблицы.

9. Итерационный процесс следует продолжить до тех пор, пока не выполнится условие

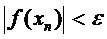, (5.4)

Тогда за приближенное решение уравнения (5.1) с точностью ε принимается n-я итерация, т.е.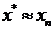

Условное форматирование.

Чтобы сделать наглядным окончание итерационного процесса воспользуйтесь Условным форматированием. Для этого выделите блок ячеек Е7:Е12, и выполните команду меню Формат\Условное форматирование,

в открывшимся окне сделайте установки, как показано на рис.8. Цвет заливки определите, нажав кнопку Форомат.

Рис.8.

Результат такого форматирования виден на рис.7. Ячейки столбца Е, значения которых удовлетворяют условию (5.4) тонированы.

Таким образом, за приближенное решение уравнения (5.1) с заданной точностью ε =0,01 по методу касательных принимается 2-я итерация, т.е. x^*»1,767.

Измените значение ε, т.е. содержимое ячейки Е3, и вы увидите как изменится значение корня нашего уравнения. Проанализируйте результаты и вы получите ответ на пункт задания 5.2.

Метод хорд.

Исходя из начального приближения x₀, удовлетворяющего условию

f(x₀) f ^’’ (x₀)<0, (5.5)

корень x^* уравнения (5.1) с заданной точности ε вычисляется по формуле

. (5.6)

или

, (5.7)

В нашем случае условие (5.5) выполняется для х₀=а=1 (см.рис.6). Поэтому для построения итерационного процесса используем формулу (5.7).

Порядок решение аналогичен предыдущему методу касательных, поэтому рекомендуется внимательно ознакомиться с материалом пункта 5.1. Расчетная схема метода хорд приведена на рис.9.

За приближенное решение уравнения (5.1) по методу хорд с заданной точностью ε=0,01 принимается 4-я итерация, т.е. x^* »1,7618.

Рис.9.

Измените значение ε, т.е. содержимое ячейки D4, и вы увидите, как изменится значение корня нашего уравнения. Проанализируйте результаты и вы получите ответ на пункт задания 5.2.

Метод половинного деления (дихотомии).

Делим отрезок [a, b] пополам. Из двух отрезков [a, (a+b)/2] и [(a+b)/2, b] выбираем тот, на концах которого функция f(x) имеет разные знаки. Новый, уменьшенный вдвое, отрезок называем тем же именем [a, b] и снова делим пополам. Продолжая этот процесс, получим систему вложенных друг в друга отрезков.

Деление отрезков продолжаем до тех пор, пока длина последнего не станет меньше заданного ε, т.е. до тех пор, пока не выполнится условие:

. (5.8)

Тогда за приближенное решение уравнения (5.1) с точностью ε принимается