Свойства конъюнкции, дизъюнкции и отрицания
Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам обычных операций умножения и сложения. Легко убедится в том, что для этих функций выполняются сочетательный
x1&(x2&x3)= (x1&x2)&x3,
x1  (x2
(x2  x3)= (x1
x3)= (x1  x2)
x2)  x3,
x3,
переместительный
x1  x2= x1
x2= x1  x2,
x2,
x1& x2= x1&x2,
и распределительный законы. Кроме того, выполняется распределительный закон дизъюнкции относительно конъюнкции.
x1  (x2&x3)= (x1
(x2&x3)= (x1  x2)& (x1
x2)& (x1  x3).
x3).
Проверим справедливость этого закона путем сравнения таблиц для функций, стоящих в левой и правой частях рассматриваемого соотношения.
| x 1 | x 2 | x 3 | x2&x3 | x1  (x2&x3) (x2&x3) |
| x 1 | x 2 | x 3 | x1  x2 x2 | x1  x3 x3 | (x1  x2)& (x1 x2)& (x1  x3) x3) |
Совпадение построенных таблиц доказывает наше утверждение.
Рассмотрим теперь ряд простых, но весьма важных соотношений
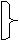 х
х  х=х;
х=х;
х&х=х.
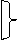
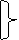
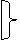 х
х  1=1; х
1=1; х  0=х; х
0=х; х 
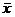 =1;
=1;
х&1=х. х&0=0. х& 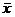 =0.
=0.
И как следствие получаем
х  х
х  …
…  х=х,
х=х,
х&х&…&х=х.
Как обобщение формул получаем следующие формулы, называемые формулами (законами) де Моргана
х1  х2
х2  …
…  хn=
хn= ;
;
х1&х2&…&хn=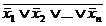 .
.
Свойства функций сложения по модулю 2, импликации, штриха Шеффера и стрелки Пирса (функции Вебба)
Свойства функции сложения по модулю 2 и функции импликации часто бывают полезными при анализе и синтезе различных дискретных устройств.
Для функции сложения по модулю 2 выполняются переместительный и сочетательный законы, а также распределительный закон относительно конъюнкции:
x1 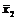 x2= x2
x2= x2 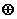 x1;
x1;
x1 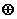 (x2
(x2 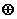 x3)= (x1
x3)= (x1 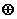 x2)
x2) 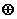 x3;
x3;
x1&(x2 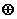 x3)= (x1&x2)
x3)= (x1&x2) 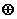 ( x1&x3).
( x1&x3).
Справедливы также очевидные соотношения
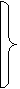 x
x 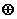 x=0;
x=0;
x 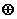 0=х;
0=х;
x 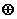 1=
1= 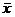 ;
;
х 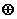
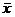 =1.
=1.
Кроме того, выполняется формула х1  х2= x1
х2= x1 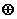 x2
x2 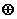 x1&x2.
x1&x2.
В отличие от всех ранее рассмотренных функций для импликации не выполняются переместительный и сочетательный законы, однако справедливы следующие соотношения:
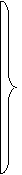 х®x=1;
х®x=1;
x® 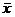 =
= 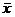 ;
;
x®1=1;
х®0= 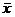 ;
;
0®х=1;
1®х=х;
х1®х2= 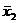 ®
® 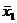 ;
;
х1®х2® х1= х1.
Функции дизъюнкции и конъюнкции могут быть выражены через импликацию следующим образом:
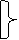 х1
х1  х2=
х2= 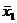 ® х2;
® х2;
х1&х2= 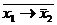 .
.
Для функции Шеффера и Вебба справедлив переместительный закон:
х1 /х2= х2/х1;
х1¯х2= х2¯х1.
Сочетательный закон для них не выполняется:
х1/(х2/х3)¹(х1/х2)/х3 ;
х1¯( х2¯х3)¹ (х1¯ х2)¯ х3.
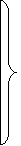 Справедливы следующие очевидные соотношения, проверка которых аналогична приведенным выше примерам и осуществляется при помощи таблиц истинности:
Справедливы следующие очевидные соотношения, проверка которых аналогична приведенным выше примерам и осуществляется при помощи таблиц истинности:
х /х= 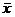 , х¯ х=
, х¯ х= 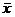 ;
;
х/ 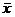 =1, х¯
=1, х¯ 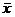 =0;
=0;
х/1= 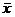 , х¯1 =0;
, х¯1 =0;
х/0=1, х¯0= 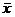 ;
;
х1/х2=  =
= 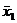

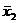 ;
;
х1¯х2= 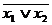 =
= 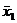 &
& 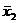 .
.
Функции Шеффера и Вебба связаны между собой соотношениями, аналогичными формулами де Моргана для функций конъюнкции и дизъюнкции:
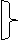 х1/х2=
х1/х2=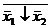 ;
;
х1¯х2=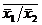 .
.
ОСНОВНЫЕ КЛАССЫ ФАЛ
В качестве первого класса таких ФАЛ рассмотрим класс функций, сохраняющих константу нуль, т.е. таких функций, для которых справедливо равенство
f (0, 0, …, 0)=0
Очевидно, что в фиксированном множестве число функций этого класса составляет половину всех функций алгебры логики, т.е. 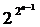 функций.
функций.
Аналогично класс функций, сохраняющих константу единица, будет определен, как класс функций, для которых выполняется равенство
f (1, 1,…, 1)=1
Этот класс состоит также из 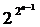 функций.
функций.
Определение Функция f*(x1 ,…,xn) называется двойственной к функции f (x1 ,…,xn), если выполняется равенство
f*(x1 ,…,xn)= 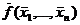 .
.
Определение Функция . f (x1 ,…,xn) самодвойственный, если она совпадает с двойственной себе функцией, т.е. справедливо равенство
f (x1 ,…,xn )= 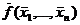 .
.
Определение ФАЛ f(x1,…,xn ) называется линейной, если она представима в следующем виде
f (x1 ,…,xn )=с0 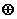 с1х1
с1х1 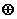 …
… 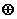 сnхn,
сnхn,
где коэффициент сi 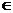 {0, 1}.
{0, 1}.
Число членов этого класса 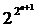 .
.
Определение ФАЛ f(x1,…,xn ) называется монотонной, если для любых двух наборов Х1 и Х2 таких, что Х1³ Х2 выполняется равенство
f (X1)³f (X2)
X1=< 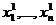 >
>
X2=< 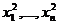 >.
>.
Определение ФАЛ f(x1,…,xn ) называется симметричной, если она не изменяется при произвольной перенумерации аргументов.
f(x1,…,xn )= f(y1,…,yn ),
где (y1,…,yn) – любая перестановка аргументов (x1,…,xn ).
АНАЛИТИЧЕСКАЯ ЗАПИСЬ ФАЛ
Пусть имеется двоичный набор < 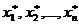 >. Сопоставим ему число i, определяемое
>. Сопоставим ему число i, определяемое
i= 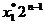 +
+ 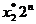 +…+
+…+  ,
,
число i называют номером набора < 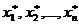 >.
>.
Рассмотрим функцию F(x1,…,xn), определяемую следующим соотношением
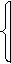 1, если номер набора i
1, если номер набора i
(0) Fi=
0, в противном случае.
Такую функцию называют характеристической функцией «единицы». Предположим, что удалось построить аналитическое выражение для функции Fi (как это можно сделать описывается ниже). Тогда справедлива следующая теорема.
Теорема. Любая таблично заданная функция ФАЛ может быть задана в следующей аналитической форме
(1) f(x1,…,xn )= 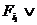
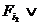 …
… 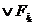 =
= 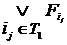 ,
,
где Ti – множество номеров наборов, на которых функция обращается в единицу.
Справедливость этой теоремы вытекает из следующего. Возьмем произвольный набор аргументов из таблицы, задающей функцию. Возможны два случая:
1. Если на этом наборе функция равна единице, то в правой части соотношения (1) найдется  , у которой ij соответствует номеру рассматриваемого набора. Но тогда на основании (0) на данном наборе
, у которой ij соответствует номеру рассматриваемого набора. Но тогда на основании (0) на данном наборе  будет равно единице.
будет равно единице.
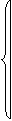 В силу хÚ1=1
В силу хÚ1=1
х •1 = 1
х  0=х
0=х
х&0 =0
х 
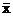 =1
=1
х • 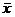 =0.
=0.
при этом вся правая часть (1) будет также равна единице. Если же на рассматриваемом наборе функция f(x1,…,xn )=0, то как следует из формулировки теоремы, среди характеристических функций  не будет такой, у которой индекс совпадает с номером рассматриваемого набора аргументов. Все члены дизъюнкции будут равны 0 в правой части. Мы доказали, что левая и правая часть соотношения (1) совпадают на любом наборе.
не будет такой, у которой индекс совпадает с номером рассматриваемого набора аргументов. Все члены дизъюнкции будут равны 0 в правой части. Мы доказали, что левая и правая часть соотношения (1) совпадают на любом наборе.
2. В теореме (1) мы воспользовались дизъюнкцией характеристических функций. Выясним, нельзя ли вместо дизъюнкции использовать какую-либо другую ФАЛ. Для того, чтобы выполнялось соотношение, подобное (1), необходимо, чтобы при обращении любой из характеристических функций в «1» все выражение обращалось в «1», а при нулевых значениях (0) все выражение становилось равным 0.
Если обозначить неизвестную операцию значком 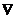 , то сформулированное нами условие представимо в виде таблицы.
, то сформулированное нами условие представимо в виде таблицы.
| Fi Fj | Fi 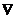 Fj Fj | Fi Fj | Fi 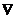 Fj Fj | |
| 0 0 | 1 0 | |||
| 0 1 | 1 1 | (?) |
Искомая функция 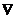 может быть определена двумя различными способами. Если в ее определяющую таблицу вместо (?) дописать «1», то полученная функция будет дизъюнкцией. Этот случай рассматривается в теореме (1). Если же (?) заменить «0», то мы получим функцию сложения по модулю 2.
может быть определена двумя различными способами. Если в ее определяющую таблицу вместо (?) дописать «1», то полученная функция будет дизъюнкцией. Этот случай рассматривается в теореме (1). Если же (?) заменить «0», то мы получим функцию сложения по модулю 2.
Следствие. Любая таблично заданная ФАЛ может быть представлена в следующей аналитической форме
(2) f(x1,…,xn )= 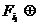
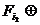 …
… 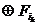 =
=  .
.
Представление функции в виде (1) будем называть дизъюнктивным, а представление в виде (2) – полиномиальным.
Для получения представлений другого типа рассмотрим функцию Фi(x1, x2,…,xn).
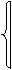 0, если номер набора равен i
0, если номер набора равен i
(3) Фi=
1, в противном случае
такие функции называют характеристическими функциями нуля. Из (1) и (3) следует
Fi(x1,…,xn)= 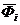 (x1,…,xn).
(x1,…,xn).
Теорема.
Любая таблично заданная ФАЛ может быть задана в следующей аналитической форме
(4) f(x1,…,xn )= 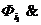
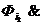 …
… 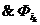 =
= 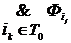 ,
,
где T0 – множество номеров наборов, на которых функция f обращается в нуль.
Представление функции в виде (4) называют конъюнктивным представлением.
Следствие. Любая таблично заданная ФАЛ может быть представлена в следующей форме
f(x1,…,xn )= 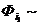
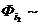 …
… 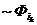 , где ij
, где ij 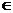 T0 .
T0 .
Перейдем теперь к аналитическому выражению самих характеристических функций.
Условимся о ряде обозначений. Введем в рассмотрение «степень» аргумента х, которую будем обозначать 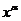 .
.
Положим, что
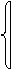 х,
х, 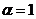
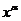 =
=
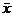 ,
, 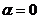 .
.
Рассмотрим конъюнкцию
(5) 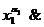
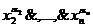 .
.
Набор < 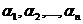 > двоичный и существует равно 2n различных таких наборов. Таким образом, число различных конъюнкций также равно 2n.
> двоичный и существует равно 2n различных таких наборов. Таким образом, число различных конъюнкций также равно 2n.
Сопоставим каждой конъюнкции (5) номер, определяемый номером набора < 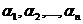 >.
>.
Тогда запись 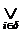 (
( 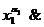
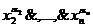 )i , означает дизъюнкцию всех конъюнкций с номерами из множества δ.
)i , означает дизъюнкцию всех конъюнкций с номерами из множества δ.
Аналогично запись
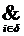 (
( 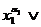
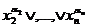 )i , i
)i , i 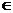 δ
δ
означает конъюнкцию всех дизъюнкций с номерами из множества δ.
Покажем, что 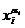 =1 тогда и только тогда, когда выполняется равенство
=1 тогда и только тогда, когда выполняется равенство
xi=αi.
Это вытекает из рассмотрения следующих четырех возможных случаев:
1. 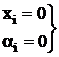
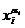 =
= 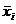 =1 2.
=1 2. 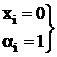
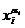 =xi=0
=xi=0
3. 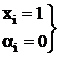
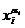 =
= 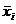 =0 4.
=0 4. 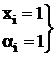
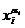 =xi=1
=xi=1
Таким образом, конъюнкция 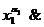
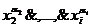 , не обращается в 0 только в том случае, если одновременно выполняются следующие i равенств:
, не обращается в 0 только в том случае, если одновременно выполняются следующие i равенств:
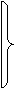 x1=α1
x1=α1
(6) x2=α2
……
xi=αi
Из (6) вытекает, что
Fi (x1,…,xn )= 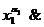
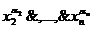 , при условии, что
, при условии, что
i= 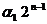 +
+ 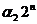 +…+
+…+ 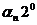 .
.
Тогда на основании теоремы (1) можно утверждать, что любая функция алгебры логики, кроме нуля, может быть представлена в следующей форме:
(7) f (x1, x2, …, xn )= 
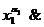
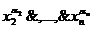 .
.
При этом дизъюнкция в правой части берется только по тем номерам наборов аргументов, по которым функция, заданная таблично, обращается в единицу.
Представление ФАЛ в виде (7) называют совершенной дизъюнктивной нормальной формой этой функции (СДНФ).
Данная теорема позволяет сформулировать алгоритм перехода от табличного задания функции к записи этой функции в виде СДНФ. Этот алгоритм формулируется следующим образом:
1. Выбрать в таблице задания функции все наборы аргументов, на которых функция обращается в единицу.
2. Выписать конъюнкции, соответствующие этим наборам аргументов. При этом, если аргумент xi входит в данный набор как «1», он вписывается в конъюнкцию, соответствующую данному набору, без изменения. Если же xi входит в данный набор как «0», то в соответствующую конъюнкцию вписывается его отрицание.
3. Все полученные конъюнкции соединяются между собой знаками дизъюнкции.
Пример:пусть задана функция f(x1, x2, x3) следующей таблицей:
| x1 | x2 | x3 | f(x1, x2, x3) |
Требуется получить из нее совершенно дизъюнктивную нормальную форму.
Для нахождения ДСНФ выбираем из таблицы только те строки, в которых стоят наборы значений аргументов, обращающих функцию в единицу (это 4, 5, и 7 строки). Выписываем конъюнкции, соответствующие выбранным строкам:
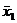 & x2&x3, x1&
& x2&x3, x1& 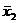 &
& 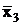 , x1& x2&
, x1& x2& 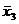 .
.
Соединяя эти конъюнкции знаками дизъюнкции, окончательно получаем
f(x1, x2, x3)= 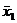 x2x3
x2x3  x1
x1 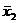 x3
x3  x1x2
x1x2 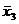 .
.
Итак, можно отметить необходимые и достаточные условия совершенной нормальной дизъюнктивной формулы. СДНФ формулы f (x1, x2, …, xn ), содержащие n различных переменных, обладают следующими свойствами:
А) в ней нет двух одинаковых слагаемых;
Б) ни одно слагаемое не содержит двух одинаковых множителей;
В) никакое слагаемое не содержит переменную вместе с ее отрицанием;
Г) в каждом слагаемом содержится в качестве множителя либо переменная хi, либо ее отрицание 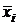 , где i=1,2,…,n.
, где i=1,2,…,n.
Д) число множителей равно числу n.
Если вместо (1) воспользоваться соотношением (2), получим полиномиальную совершенную нормальную функцию (ПСНФ).
Так для функции, рассмотренной в примере, ПСНФ имеет следующий вид:
f(x1, x2, x3)= 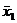 & x2&x3
& x2&x3 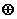 x1&
x1& 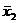 &
& 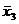
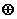 x1& x2&
x1& x2& 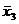 .
.
Кроме представления ФАЛ в СДНФ, возможно представление ее в некоторой другой форме, двойственной по отношению к СДНФ.
Теорема. Любая ФАЛ, кроме единицы, может быть представлена в следующей форме:
(8) f(x1, x2, x3)=  (
( 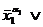
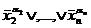 ).
).
Символ  означает, что конъюнкция берется только по тем наборам, <
означает, что конъюнкция берется только по тем наборам, < 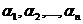 >, для которых выполняется равенство:
>, для которых выполняется равенство:
f(x1, x2, x3)=0.
Доказательство теоремы.
На основании предыдущей теоремы имеем
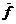 (x1, x2,…, xn)=
(x1, x2,…, xn)= 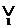
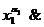
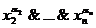
или 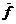 (x1, x2,…, xn)=
(x1, x2,…, xn)= 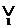
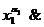
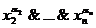 &
& 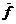 (
( 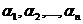 ).
).
Как известно, равенство не нарушается, если от обеих его частей взять отрицание:
f (x1, x2, …, xn )= 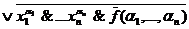 .
.
Согласно закону де Моргана
f (x1, x2, …, xn )= 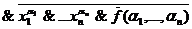 =&(
=&( 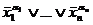 )
)  f(
f( 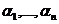 ).
).
На тех наборах, для которых f( 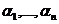 )=1 соответствующая дизъюнкция
)=1 соответствующая дизъюнкция
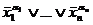
 f(
f( 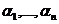 )=1.
)=1.
В силу х  1=1 такие наборы на значение конъюнкции не влияют и ими можно пренебречь:
1=1 такие наборы на значение конъюнкции не влияют и ими можно пренебречь:
f (x1, x2, …, xn )= 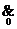 (
( 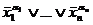 ).
).
Теорема доказана для всех n³1.
Представление ФАЛ в виде (8) носит название совершенной конъюнктивной нормальной формы(СКНФ).
Из теоремы вытекает алгоритм построения КСНФ:
1. Выбрать в таблице задания функции все наборы аргументов, на которых функция обращается в нуль.
2. Выписать дизъюнкции, соответствующие этим наборам аргументов. При этом, если аргумент xi входит в данный набор как «0», он вписывается без изменения в дизъюнкцию, соответствующую данному набору. Если же xi входит в данный набор как «1», то в соответствующую дизъюнкцию вписывается его отрицание.
3. Все полученные дизъюнкции соединяются между собой знаками конъюнкций.
Пример.
Написать СКНФ для функции, заданной следующей таблицей.
| x1 | x2 | x3 | f(x1, x2, x3) |
f(x1, x2, x3)= (x1  x2
x2  x3)&(x1
x3)&(x1 
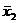

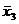 )&(
)&( 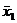

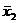

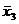 ).
).
Аналогично СДНФ, можно отметить необходимые и достаточные условия совершенной нормальной конъюнктивной формулы. СКНФ формулы f(x1, x2, …, xn ), содержащие n различных переменных, обладают следующими свойствами:
А) в ней нет двух одинаковых множителей;
Б) ни один множитель не содержит двух одинаковых слагаемых;
В) ни один множитель не содержит какой-нибудь переменной вместе с ее отрицанием;
Г) каждый множитель содержит в качестве слагаемого или хi, или ее отрицание 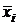 , где i=1,2,…,n.
, где i=1,2,…,n.
Д) число слагаемых равно числу n.
Как следует из алгоритмов построения СДНФ и СКНФ выбор той или иной формы аналитической записи определяется видом таблицы заданной функции. Если большинство значений нулевое, то выгодно записывать в СДНФ, в противном случае более экономичную запись дает СКНФ.
Итак, если в каждом члене нормальной формы представлены все переменные (либо в прямом, либо в инверсном виде), то она называется совершенной нормальной формой.
Можно показать, что любая булева функция, не являющаяся тождественным нулем (единицей) имеет одну и только одну совершенную дизъюнктивную (конъюнктивную) нормальную форму.
Если какой-либо член φ дизъюнктивной (конъюнктивной) функции не содержит переменной xi , то она вводится тождественным преобразованием
для получения СДНФ φ = φ&( xi 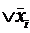 )= φ xi
)= φ xi 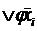 ,
,
и для СКНФ соответственно φ 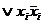 =( φ
=( φ  xi)( φ
xi)( φ 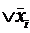 ).
).
В силу тождеств φ  φ= φ и φ φ= φ одинаковые члены, если они появляются, заменяются одним таким членом.
φ= φ и φ φ= φ одинаковые члены, если они появляются, заменяются одним таким членом.
Приведем соотношения эквивалентных преобразований, полезных при упрощении формул:
Законы склеивания
1) 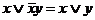 ;
;
2) 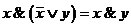 ;
;
3)  ;
;
4) 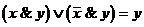 .
.
Законы поглощения
1) 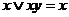 ;
;
2)  ;
;
3) 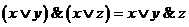 .
.
Правила:
1. Если слагаемое некоторой суммы входит в другое слагаемое, то это второе слагаемое можно из суммы удалить.
2. Если множитель некоторого произведения входит слагаемым в другой множитель, то второй множитель можно удалить.
3. В каждом слагаемом можно удалить множитель, который равносилен отрицанию другого слагаемого.
4. В каждом множителе можно удалить слагаемое, которое равносильно отрицанию другого множителя.
Пример.
1. Заданную функцию f(x,y,z)=x 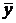 z
z  x
x 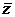 привести к СДНФ:
привести к СДНФ:
x 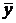 z
z  x
x 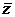 = x
= x 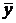 z
z  x
x 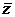 (y
(y 
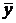 )= x
)= x 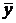 z
z  xy
xy 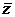
 x
x 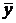
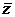 ;
;
2. Задана функция f(x,y,z)= 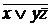 (x
(x  z). Необходимо привести к СКНФ.
z). Необходимо привести к СКНФ.
f(x,y,z)= 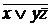 (x
(x  z)=
z)= 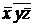 (x
(x  z)=
z)= 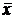 (x
(x  z)(
z)( 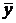
 z).
z).
Добавить к каждому члену соответственно y 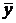 , x
, x 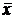 , z
, z 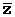
= 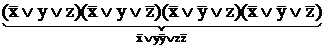 •
• 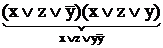 •
• 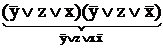 =
= 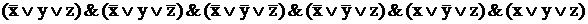 .
.
Полная система функций.
Определение. Система ФАЛ (f1, f1,…, fm) называется полной, если любая функция может быть представлена суперпозицией функций f1, f1,…, fm.
Система функций { f1, f1,…, fm }, являющаяся полной, называется базисом.
Примеры полных систем функций: x1x2; x1  x2 ; x1
x2 ; x1 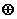 x2 ; x1x2=
x2 ; x1x2=  .
.
Минимальным базисом называется такой базис, для которого удаление хотя бы одной функции f1 , образующей этот базис, превращает систему функций (f1, f1,…, fm) в неполную.
Любая функция, как было показано ранее, может быть представлена в виде СДНФ или СКНФ:
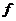 (x1, x2,…, xn)=
(x1, x2,…, xn)= 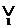
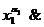
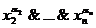
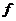 (x1, x2,…, xn)=
(x1, x2,…, xn)= 
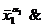
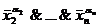 .
.
Верно утверждение о полноте системы, состоящей из трех функций: конъюнкции, отрицания и дизъюнкции.
Минимизация функций алгебры логики
Любая ФАЛ может быть записана в виде СДНФ или СКНФ. Покажем на примере, что такая запись в ряде случаев является неэкономной.
Пример. Пусть задана ФАЛ в СДНФ.
f(x1, x2, x3)= 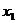 & x2&x3
& x2&x3  x1& x2&
x1& x2& 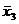
 x1&
x1& 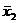 & x3
& x3  x1&
x1& 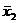 &
& 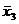

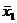 & x2& x3.
& x2& x3.
Добавим к функции один конъюнктивный член 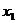 & x2&x3. Это добавление не меняет данной функции так как x
& x2&x3. Это добавление не меняет данной функции так как x  x=x:
x=x:
f(x1, x2, x3)= 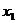 x2x3
x2x3  x1 x2
x1 x2 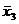
 x1
x1 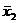 x3
x3  x1
x1 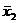
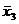

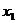 x2x3
x2x3 
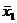 x2x3.
x2x3.
Преобразуем это выражение, используя сочетательные и распределительные свойства конъюнкции и дизъюнкции:
f(x1, x2, x3)= 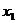 x2 (x3
x2 (x3 
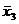 )
)  x1
x1 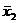 ( x3
( x3 
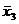 )
)  x2 x3 (x1
x2 x3 (x1 
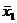 ).
).
Исполь
