Комбинации случайных независимых событий
1. Определение вероятности того, что из двух независимых и несовместимых событий А и В произойдет хотя бы одно А или В, то есть вероятности суммы независимых и несовместимых событий Р(А + В). Для простоты здесь и в дальнейшем используется классическое определение вероятности. Если из общего числа возможных случаев N и М1 случаях происходит событие А, а в других М2 случаях происходит событие В, то
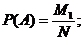 (1)
(1)
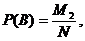 (2)
(2)
причем случаи, входящие в число М1, не входят в М2 и, наоборот, так как события несовместимы. Вероятность того, что произойдет одно из событий А и В, очевидно, равна
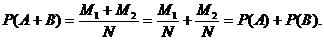 (3)
(3)
Эта формула распространяется на сумму произвольного числа несовместимых событий
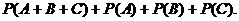 (4)
(4)
2. Вероятность суммы противоположных событий равна 1.
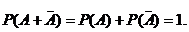 (5)
(5)
Так как одно из событий 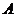 или
или 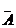 обязательно произойдет, то сумма их есть достоверное событие, вероятность чего равна 1. Как следствие:
обязательно произойдет, то сумма их есть достоверное событие, вероятность чего равна 1. Как следствие:
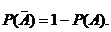 (6)
(6)
3. Вероятность полной группы несовместимых событий равна 1, так как одно из них обязательно произойдет.
4. Определим вероятность суммы двух независимых совместимых событий А и В. Пусть из общего числа N случаев в М1 случаях имеет место только событие А, в М2 слу-
чаях имеет место только событие В, а в М3 случаях имеет место как событие А, так и событие В одновременно.
Тогда
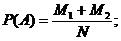
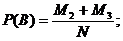
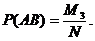
Очевидно, общее число случаев, когда имеет место событие А или В (хотя бы одно из них), составляет
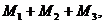
то есть вероятность суммы двух совместимых событий составляет
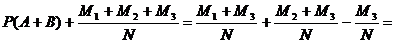
(7)
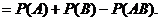
Следовательно, вероятность суммы событий А и В равна сумме вероятностей этих событий минус вероятность их одновременного возникновения. Так как 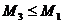 и
и 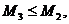
то 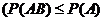 и
и 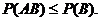
5. Определим вероятность одновременного возникновения двух независимых и совместимых событий А и В, то есть Р(АВ). Пусть событие А может иметь место в М1 случаях из общего числа N1 случаев возникновения или невозникновения события А, а событие В в М2 случаев из общего числа N2. Тогда
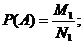
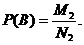
Для любого случая из указанного числа N1 может иметь место N2 различных случаев возникновения или невозникновения события В. Всего число возможных случаев составляет
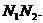
Для каждого случая возникновения события А, а число таких случаев М1, может иметь место М2 случаев одновременного возникновения события В. Всего число случаев одновременного возникновения А и В будет М1М2. Поэтому вероятность одновременного возникновения событий А и В равна
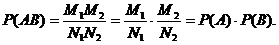 (8)
(8)
При несовместимости событии А и В 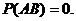
Поэтому вероятность возникновения хотя бы одного из независимых совместимых событий А и В составляет
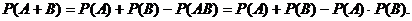 (9)
(9)
Основные законы вероятностей комбинации
Зависимых случайных событий
Условной вероятностью события А по отношению к событию В называется вероятность события А при условии, что событие В имеет место. Она обозначается Р(А/В). Если событие А и В взаимозависимые, то Р(А/В) отличаются от Р(А). Если же Р(А/В)=Р(А), то события А и В независимы.
1. Определим, чему равна условная вероятность Р(А/В). Используем для простоты классическое определение вероятности. Пусть из общего числа случаев N событие А наступает в М случаях, событие В в К случаях и событие АВ (одновременное наступление событий А и В) в R случаях.
Очевидно, что R £ М и R £ К.
Событие В имеет место только в К случаях и при этом только в R из К случаев имеет место событие А. Поэтому условная вероятность события A по отношению к В равна
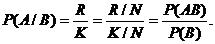 (10)
(10)
2. Вероятность одновременного наступления двух зависимых событий равна в силу указанного в п. 1.
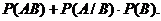 (11)
(11)
Если событие А и В независимы, то
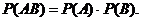 (12)
(12)
3. Для трех взаимосвязанных событий вероятность одновременного их возникновения равна
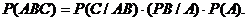 (13)
(13)
4. Если событие А не зависит от В, то и событие В не зависит от А; в первом случае 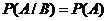
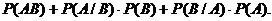
Заменяя в силу заданного условия 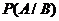 на
на 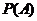 , получим
, получим
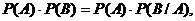
то есть
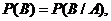
то есть, событие В не зависит от А.
5, Вероятность сложного события А, подразделяемого на частные случаи В1, В2 и В3, при зависимости А от В1, В2 и В3 равна
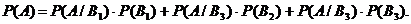 (14)
(14)
Эта формула называется формулой полной вероятности.
Тема 4
Категории электроприемников и обеспечение
