Числовые и функциональные ряды.

Числовым рядом называется формальное выражение вида

,

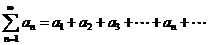где число слагаемых 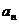неограниченно. Выражение 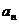называется общим, или -ным, членом ряда. Сумме бесконечного числа слагаемых нужно придать смысл. Делается это следующим образом. Назовем –ной частичной суммой ряда 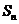сумму первых слагаемых

.

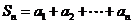Суммой ряда 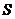называется предел частичных сумм

.

Ряд с конечной суммой называется сходящимся. Если предела частичных сумм не существует, говорят, что ряд расходится.

Найти сумму ряда точно почти никогда не удается. В действительности важно знать, сходится ли ряд вообще, или нет. Именно этот вопрос нас и будет интересовать.

Необходимое условие сходимости ряда

.

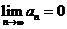Ряд называется знакоопределенным, если все слагаемые имеют один знак. Имеется несколько простых достаточных условий сходимости знакоположительных рядов.

Признак Даламбера. Пусть существует предел

.

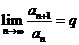Тогда, если 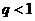, то ряд 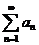сходится; если 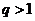, то ряд расходится.

Признак Коши (радикальный). Пусть существует предел

.

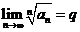Если 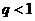, то ряд 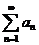сходится, если 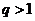, то ряд 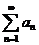расходится.

Признак Коши (интегральный). Если найдется такая монотонно убывающая положительная функция , что 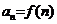для всех 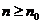, то тогда из сходимости интеграла 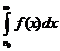следует сходимость ряда 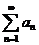, а из расходимости интеграла 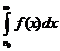следует расходимость ряда .

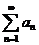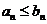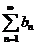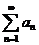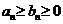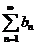Иногда для исследования сходимости знакоположительного ряда удобно использовать признаки сравнения. Если и ряд сходится, то и сходится. Если и ряд расходится, то и 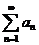расходится.

Из признаков сходимости знаконеопределенных рядов нам потребуется признак Лейбница сходимости знакочередующегося ряда. Если мы имеем ряд

,

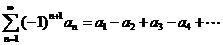где 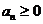, 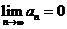и при этом 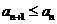, то ряд 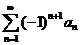сходится. Для рядов, удовлетворяющих условию Лейбница (то есть знакочередущихся рядов, у которых монотонный предел модуля –го члена равен нулю), имеется следующая полезная оценка:

,

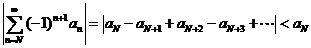то есть остаток ряда, начиная с произвольного члена 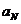, по модулю не превосходит этого члена.

Задача 4.3.аИсследовать сходимость ряда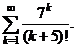

Решение. Имеем 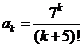, , 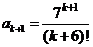и, по признаку Даламбера,

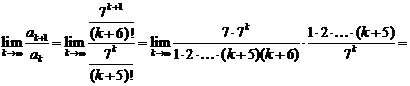
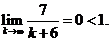Следовательно, ряд сходится.

Задача 4.3.бИсследовать сходимость ряда .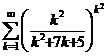

Решение. Имеем: 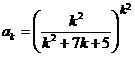, и, по радикальному признаку Коши,

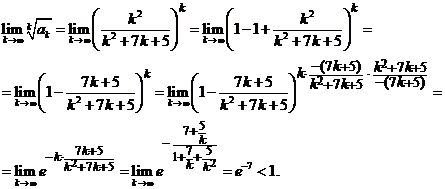Следовательно, ряд сходится.

Задача 4.3.вИсследовать сходимость ряда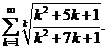

Решение. Имеем:

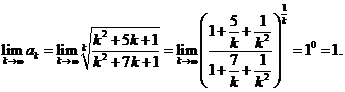
Следовательно, не выполнено необходимое условие сходимости ряда 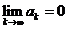и ряд расходится.

Задача 4.3.гИсследовать сходимость ряда .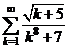

Решение. Подберем ряд для сравнения. С учетом неравенств 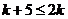, , 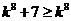выполненных при всех 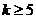, имеем

.

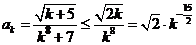Для ряда 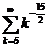воспользуемся интегральным признаком Коши. Положим 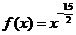. Тогда

.

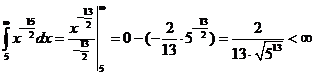Следовательно, и ряд 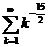, и ряд 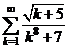сходятся.

Функциональным рядом называется выражение вида

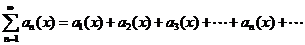
Для каждого фиксированного значения параметра сходимость ряда определяется как предел частичных сумм соответствующего числового ряда. Область сходимости – множество значений , при которых ряд сходится. Для степенного ряда

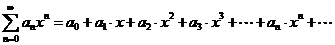
областью сходимости является интервал 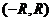, где 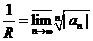. Здесь 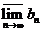обозначает верхний предел последовательности 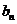, то есть наибольший из пределов всех сходящихся подпоследовательностей 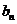. Внутри данного интервала ряд сходится абсолютно (то есть сходится ряд, составленный из модулей членов). Сходимость степенного ряда в граничных точках 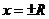исследуется отдельно.

Рядом Тейлора функции в точке называется степенной ряд

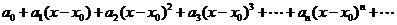
где

.

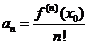Если значение равно сумме ее ряда Тейлора 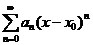, то функция называется аналитической в точке . Ряд Тейлора определен однозначно в том смысле что, если 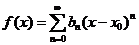для какого-либо степенного ряда, то тогда 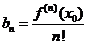. Степенные ряды внутри области сходимости можно почленно дифференцировать и интегрировать: если 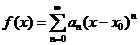, то тогда

,

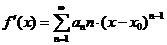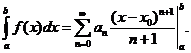
Задача 4.4. Выписать ряд Тейлора функции 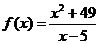с центром в точке 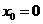. Найти область сходимости ряда.

Решение. Воспользуемся формулой суммы бесконечной геометрической прогрессии:

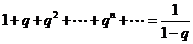при .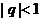

Для этого сначала поделим с остатком числитель дроби на знаменатель:

.

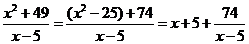Далее,

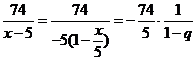где .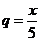

Следовательно,

.

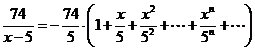Окончательно,

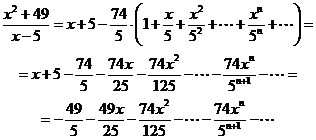
Чтобы найти область сходимости ряда, воспользуемся признаком Даламбера. Зафиксируем и рассмотрим ряд из модулей:

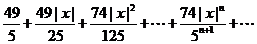
Тогда общий член ряда записывается формулой 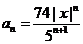, , 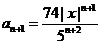и, следовательно,

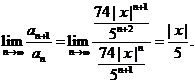
Согласно признаку Даламбера при 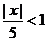ряд сходится, а при 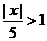ряд расходится. Интервал сходимости ряда 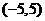. Исследуем поведение ряда в граничных точках 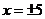. При 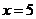получаем:

.

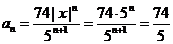Поскольку 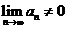, то необходимое условие сходимости ряда оказывается невыполненным, и ряд расходится. При 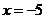ряд расходится по той же причине.

Задача 4.5. Вычислить приближенно с точностью до e=0.001 значение интеграла 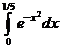, используя разложение подынтегральной функции в ряд Тейлора.

Решение. Воспользуемся формулой

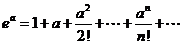
Подставляя 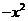вместо 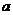, получим:

.

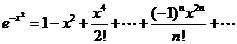Интегрируя почленно, получим

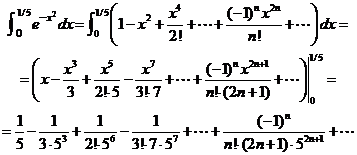
Чтобы понять, сколько членов ряда нужно взять, чтобы найти сумму ряда с точностью до 0.001, воспользуемся оценкой остатка лейбницевского ряда: сумма отброшенных слагаемых по модулю не превосходит первого отброшенного числа. Таким образом, остается решить, для какого натурального числа впервые будет выполнено неравенство

.

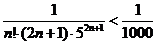Последовательно подставляя в данное неравенство значения 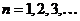, убеждаемся, что впервые неравенство оказывается выполненным при :

.

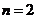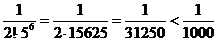В частности, все слагаемые ряда, начиная с 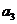, можно отбросить.

Ответ: .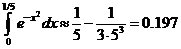

Рядом Фурье на интервале 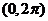называется функциональный ряд вида

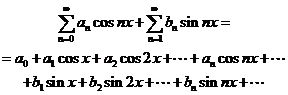
Если функция непрерывна (или имеет конечное число разрывов первого рода) на интервале , и ее производная существует всюду, кроме конечного числа точек, и при этом ограничена по модулю 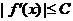, то значение в точках непрерывности равно сумме ряда Фурье

,

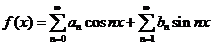коэффициенты 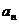и 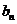которого определяются по формулам

, , , ,.

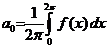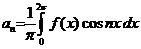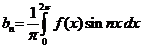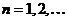Задача 4.6. Представить функцию 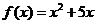рядом Фурье в интервале (0,2p).

Решение. Имеем:

.

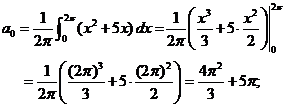
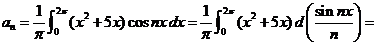
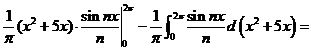
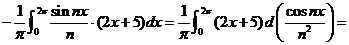
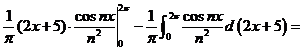
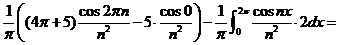
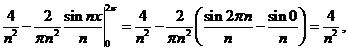
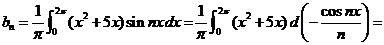
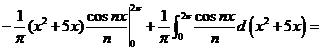
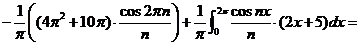
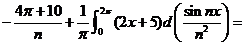
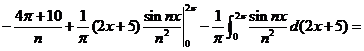
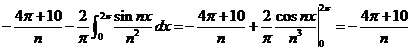Окончательно, получаем:

.

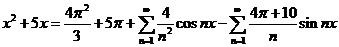Литература.

1. Щипачев В.С. Высшая математика. Учебник для вузов. - М., Высшая школа, 2001.

2. Кремер Н.Ш. Высшая математика для экономистов. Учебник. 2 издание. Юнити - Дана, 2002.

3. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М., Наука, 1984.

4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М., Наука, 1988.

5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. ТФКП. - М., Наука, 1985.

6. Клетеник Д.В. Сборник задач по аналитической геометрии. - М., Наука, 1984.

7. Борисова О.Н. Математика: Учебная программа и методические материалы. - Королев: КИУЭС, 2003, 26 с.

СОДЕРЖАНИЕ

	Раздел	Стр.
	Линейная алгебра
	Векторная алгебра и аналитическая геометрия
	Пределы
	Производная
	Функции нескольких переменных
	Интегралы
	Дифференциальные уравнения
	Ряды
	Литература
	Содержание