Общая схема исследования функций.

Задача 2.4. Исследовать функцию с помощью производных первого и второго порядка и построить её график.

Решение.Исследование функции производится по следующей схеме.

1. Общие особенности функции: область определения, непрерывность и точки разрыва, вертикальные асимптоты, четность – нечетность, периодичность.

В нашем случае область определения функции

;

прямая – вертикальная асимптота, функция общего вида.

2. Нули функции и интервалы знакопостоянства.

Применим метод интервалов для исследования знаков функции.

- + - +

7 10 20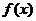

3. Возрастание – убывание функции, точки экстремума. Этот пункт связан с исследованием знаков первой производной функции. Имеем:

Корни квадратного многочлена равны

Знаки определим, используя метод интервалов.

+ - - +

8.6 20 31.4

max min

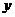
Точки и являются точками локального максимума и минимума соответственно.

4. Выпуклость – вогнутость функции, точки перегиба. Данный пункт связан с исследованием второй производной функции. Если , то функция выпукла вверх (как функция ), а если , то функция выпукла вниз (как функция ).

+

20

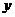
5. Наклонные асимптоты функции.

Наклонная асимптота функции (если она существует) есть такая прямая на плоскости , к которой “прижимается” график функци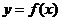и при 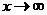, то есть . Коэффициенты и определяются из соотношений

, .

В нашем случае

Следовательно, прямая 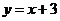является наклонной асимптотой функции.

3. Функции нескольких переменных.

Интегралы.

Частной производной функции по переменной в точке называется предел

.

Аналогично определяются частные производные по и по . При дифференцировании по одной переменной все остальные считаются постоянными.

Например, если , то

, , .

Градиентом функции называется вектор

Производной функции по направлению вектора , где , называется число

.

Теорема о полном дифференциале гласит, что

.

Поэтому

.

Если , то для взятия производной по направлению нужно предварительно нормировать вектор , поделив его на длину .

Касательная к кривой, заданной неявным уравнением , в точке определяется уравнением

.

Нормаль к той же кривой определяется уравнением

.

Задача 3.1. Найти градиент функции в точке (1,5).

Решение. Имеем:

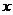Подставляя 1 вместо и 5 вместо 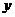, получим

.

Аналогично,

откуда . Окончательно,

.

Задача 3.2. Вычислить производную функции по направлению вектора в точке (1,1).

Решение.Длина вектора равна , поэтому перейдем к вектору , имеющему то же направление, что и вектор , но единичную длину. Далее,

, .

В точке имеем . По определению производной по направлению получаем:

.

Задача 3.3. Найти производные функции .

Решение.Имеем:

,

.

По определению вторых частных производных, имеем:

Задача 3.4. Для кривой, задаваемой уравнением , написать уравнения касательной и нормали в точке (1,1).

Решение. Подставим в уравнение касательной и нормали значения частных производных функции в точке .

, .

Уравнение касательной имеет вид:

Û .

Уравнение нормали имеет вид

Û .

Неопределенные интегралы.

Операция интегрирования является обратной к операции дифференцирования.

Определение 1. Функция 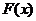называется первообразной для функции 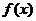, если .

У функции 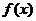имеется бесконечное множество первообразных, при этом все они отличаются друг от друга на константу: если и - две первообразные для функции 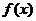, то , где С=const.

Определение 2. Множество всех первообразных для функции 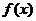называется неопределенным интегралом от 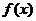и обозначается символом .

Если 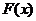- любая первообразная для 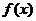, то , где С = const.