По уравнениям пространства состояния аналогового эквивалента

Цель работы

1. Определение матрицы состояния А, матрицы управления В, матрицы наблюдения С дискретной системы.

2. Определение структурных схем дискретных систем по матрицам фазовых координат.

3. Исследование структурных схем дискретных систем.

Теоретическое обоснование

Схемы моделирования дискретных систем могут быть составлены по передаточным функциям или разностным уравнениям методами:

– прямого программирования;

– параллельного программирования;

– последовательного программирования.

Полученные таким путем структурные схемы хотя и позволяют определять матрицы А, В, С и D, но характеризуются общим недостатком: ни одна из промежуточных фазовых координат системы не соответствует физическим величинам реальной системы регулирования. Поэтому может быть использован метод составления структурных схем, позволяющий так обосновать структуру дискретной модели, что ее фазовые координаты будут соответствовать физическим величинам аналоговой системы.

Этот метод основан на сравнении динамических характеристик непрерывной и дискретной моделей. В пространстве состояния непрерывная модель задается матричными уравнениями

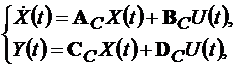(15.1)

где А_С, В_С, С_С, D_С – матрица коэффициентов состояния, управления, наблюдения и выхода дискретной системы; X(t) – фазовые координаты аналоговой системы (вектор параметров состояния); Y(t) – выходная величина аналоговой системы(вектор параметров наблюдения); U(t) – вектор параметров управления.

Получим дискретную модель по ее аналоговому эквиваленту, сохранив физический смысл аналоговых переменных состояния, только придав им дискретную форму. Запишем общее решение матричного уравнения (15.1), используя формулу Коши

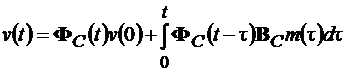, (15.2)

где v(t) – фазовая координата (параметр состояния) на интервале дискретности, m(t) – выход экстраполятора. На интервале 0 £ Т_П m(t) сохраняет постоянное m(t) = u(0). Определим v(t) в конце интервала дискретности при t = Т_П

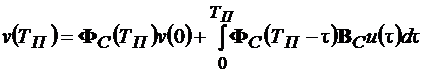(15.3)

Определим X(t) для дискретной модели в конце первого интервала дискретности, используя выражения

X(t) = AX(0) + Bu(0). (15.4)

Чтобы координаты дискретной системы совпадали с соответствующими координатами аналоговой системы, должны выполняться соотношения:

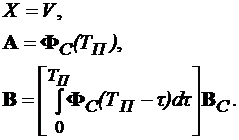(15.5)

В этом случае выражения (15.3) и (15.4) при t = Т_П будут совпадать, что приведет к совпадению дискретных фазовых координат с аналоговыми.

Выразим выходную величину аналоговой системы при t = Т_П через фазовые координаты v(t) и матрицу С_С

y(kT_П) = С_Сv(t).

Так как выходные координаты аналоговых и дискретных систем совпадают, то выполнение условия X(kT_П) = v(kT_П) приводит к С = С_С.

Описание работы

Разработаем дискретную модель системы по структурной схеме непрерывной системы (рис.15.1). Используя структурную схему (рис. 15.1А) определим матрицу состояния аналоговой системы

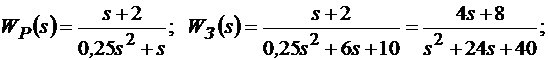
Тогда имеем

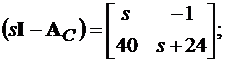
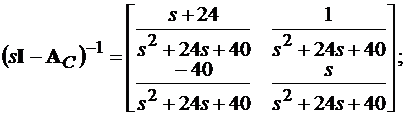
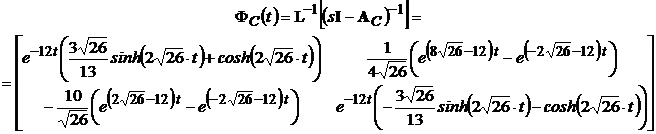
Рис. 15.1. Структурные схемы систем (А – структурная схема аналоговой модели,

В – структурная схема дискретной модели, в которой переменные состояния

соответствуют реальным физическим величинам)

Матрица А для дискретной системы принимает вид:

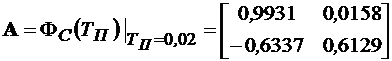. (15.6)

Для вычисление интеграла матрицы

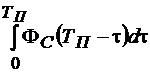(15.7)

необходимо вычислить интеграл каждого элемента этой матрицы Ф_С(t):

;

;

;

.

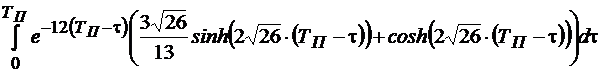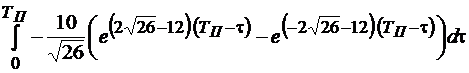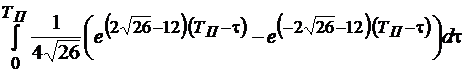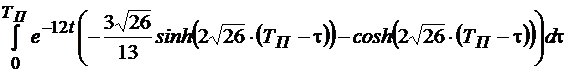Учитывая выражение (15.5) определяем для Т_П = 0,02 с матрицу управления В дискретной системы

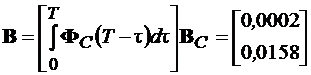. (15.8)

С учетом значений матрицы состояния А (15.6) и матрицы управления В (15.8) модель дискретной системы переменных состояния

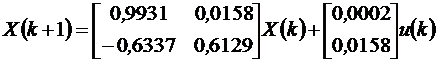. (15.9)

На рис. 15.1В приведена структурная схема дискретной системы (15.9), соответствующая аналоговому эквиваленту. На схемах рис. 15.1 совпадают выходные сигналы и промежуточные фазовые координаты, Структурные схемы аналоговой и дискретной систем совершенно не похожи, что является правилом перехода от непрерывных систем к дискретным системам в пространстве состояния. Результаты моделирования приведены на рис. 15.2.

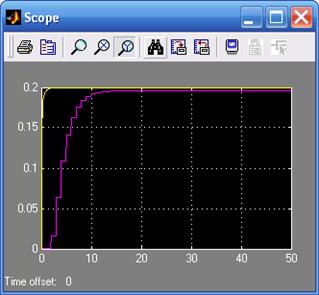
Рис. 15.2. Результаты моделирования непрерывной и дискретной систем

Вычисления, приведенные в данном примере осуществляется с помощью команды c2d по заданным матрицам A_C, B_C, C_C непрерывной системы и заданного интервала дискретности Т_П сразу определяет матрица дискретной системы, у которой все переменные состояния соответствуют реальным физическим переменным.

Определение матриц A, B, C дискретных систем соответствует алгоритму, приведенному ниже

A=[0,1;-40,-24]; %Матрицы коэффициентов замкнутой

B=[0;1];C=[8,4]; %аналоговой системы.

T=0.02; %Интервал дискретности системы

[Ad,Bd]=c2d(A,B,0.02) %Определение матриц дискретных систем

syms s %Ввод символьных переменных

Is=[s,0;0,s] %Ввод единичной матрицы

A1=inv([Is]-[A]) %Обратное преобразование Лапласа

%в частотной области

F=ilaplace(A1) %Обратное преобразование Лапласа

%во временной области

dt=0.00001;t=0:dt:0.02; %Исходные данные для вычисления

%определенных интегралов

y=-5/13*26^(1/2)*(exp((-12+2*26^(1/2))*t)-exp((-12-2*26^(1/2))*t))

%Подынтегральная функция

I1=trapz(t,y); %Вычисление определенного интеграла

Y1=-5/13*26^(1/2)*(exp((-12+2*26^(1/2))*(0.02-t))-exp((-12-2*26^(1/2))*(0.02-t))) %Подынтегральная функция

I2=trapz(t,y1) %Вычисление определенного интеграла.

Домашнее задание

1. По заданной передаточной функции непрерывной системы методом прямого программирования составить структурную схему и определить матрицы A_C, B_C, C_C.

2. Используя методику, приведенную в лабораторной работе, определить матрицы A, B, C, дискретных систем, фазовые координаты которых соответствуют реальным физическим переменным.

3. По матрицам A, B, C дискретных систем составить схему моделирования в пакете MatLab.

4. Промоделировать две системы. Сравнить фазовые координаты и сделать выводы.

Содержание отчета

1. Структурная схема непрерывной системы, определенной методом прямого программирования.

2. Подробный расчет, позволяющий обосновать матрицы A, B, C дискретной системы.

3. Структурные схемы непрерывной и дискретной систем регулирования с блоками сравнения фазовых координат системы.

4. Анализ результатов моделирования структурных схем и выводы.

Контрольные вопросы

1. Обоснуйте методику определения структурных схем непрерывных систем методом прямого программирования по передаточным функциям.

2. Как по структурным схемам непрерывных систем определить матрицы коэффициентов состояния, управления и наблюдения системы.

3. Как по структурным схемам дискретных систем определить матрицы коэффициентов состояния, управления и наблюдения системы.

4. Какие фазовые координаты структурных схем дискретных систем, полученных методами прямого программирования, параллельного программирования и последовательного программирования, совпадают с реальными физическими переменными, а какие нет.

5. Обоснуйте методику определения фундаментальной матрицы в частотной области.

6. Обоснуйте методику определения фундаментальной матрицы во временной области.

7. Обоснуйте методику составления дискретной модели, у которой фазовые координаты переменных состояния соответствуют реальным физическим переменным.

8. Какие исходные данные следует внести в программу при определении матриц дискретной системы?

9. Как в пакете MatLab определяется фундаментальная матрица для дискретной системы?

Лабораторная работа № 16

Определение параметров цифрового регулятора линейных

и нелинейных систем методом пространства состояний

Цель работы