Исследование систем регулирования в SISO Design Tool

Цель работы:

1. Изучение возможностей команды sisotool при исследовании систем регулирования.

2. Изучение взаимосвязей между расположением корней системы (метод корневого годографа), частотными характеристиками (метод логарифмических характеристик) и переходными характеристиками замкнутой системы.

3. Изучение влияний коэффициента усиления разомкнутой системы на динамические характеристики замкнутой системы.

4. Изучение влияния параметров фильтров на входе системы регулирования и в цепи обратной связи на траектории корневого годографа и на частотные и временные характеристики системы.

5. Определение влияния параметров регулятора на качество переходного процесса.

Теоретическое обоснование

Нулями передаточной функции 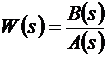называют корни уравнения B(s) = 0, то есть такие значения s, при которых передаточная функция обращается в нуль, а полюсами – корни уравнения A(s) = 0, то есть такие значения s, при которых передаточная функция обращается в бесконечность.

Звено называется минимально-фазовым, если все нули и полюса его передаточной функции имеют отрицательные или равные нулю вещественные части.

Звено называют неминимально-фазовым, если хотя бы один нуль или полюс его передаточной функции имеет положительную вещественную часть.

Связь между кривыми корневого годографа (расположением корней на плоскости корней в функции коэффициента усиления), логарифмическими характеристиками (характеризующимися частотой среза и запасом по фазе) и кривой переходного процесса (характеризующейся величиной перерегулирования) устанавливается с помощью команды sisotool.

Программой sisotool создаются структурные схемы исследуемой системы, один из вариантов которой приведен на рис. 8.1.

При выполнении программы её результат заносится в рабочее пространство MatLab (Workspace). Далее командой sisotool, записанной в главном окне MatLab, вызывается окно Import System Data, в котором представлена структурная схема исследуемой системы и поле SISO Models, в которое помещаются данные, находящиеся в рабочем пространстве MatLab. Для этого входят в меню File, а затем в подменю Import (рис. 8.2).

Рис. 8.1. Обобщающая структурная схема, исследуемая с помощью команды Sisotool

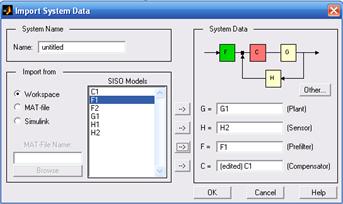
Рис. 8.2. Окно просмотра команды Import

В окне Import System Data имеются:

– список передаточных функций, находящихся в рабочем пространстве MatLab (Workspace – SISO Models);

– структурная схема исследуемой системы;

– кнопки, позволяющие содержимое Workspace поместить в соответствующие блоки структурной схемы, характеризующие данную систему.

Например, если в поле SISO Models выделить первую строку (C1), то нажатием любой из четырех кнопок со стрелками её можно поместить в один из блоков, характеризующих структурную схему. В приведенной структуре системы передаточную функцию регулятора определяет блок C, передаточную функцию объекта – блок G, передаточную функцию обратной связи – блок H, передаточную функцию фильтра – блок F. Передаточная функция объекта (G), звена обратной связи (Н) и фильтра (F) для данного эксперимента неизменна, а передаточная функция регулятора может меняться.

После ввода конкретных значений передаточных функций в структурную схему (рис. 8.2) и нажатия кнопки ОК открываются окна Siso Design Tool (рис. 8.3), в которых представлены поля для построения корневого годографа (Root Locus Editor) и логарифмических характеристик (Open–Loot Bode Editor) в функции коэффициента усиления. По корневому годографу определяют нули и полоса замкнутой системы, а по логарифмическим характеристикам – запас по фазе в градусах (P.M.: deg) и частоту среза системы (Freq: rad/sec). Численные значения нулей и полюсов можно определить более точно, выполнив вход в меню View, вход в подменю Closed-Loop Poles.

В поле Current Compensator (параметры текущего регулятора) записана передаточная функция регулятора и открыто окно для изменения коэффициента усиления разомкнутой системы K. Если внести новое значение K и щелкнуть курсором джойстика на поле корневого годографа, то в левом и правом окне будут получены новые графики, показывающие новое расположение корней замкнутой системы, новую частоту среза и новый запас по фазе.

Передаточную функцию регулятора можно усложнить, используя кнопки Add real pole (добавить реальный полюс), Add real zero (добавить реальный ноль), Add complex pole (добавить комплексные полюса), Add complex zero (добавить комплексные нули) (рис. 8.3). Если одну из кнопок сделать активной, то на поле корневого годографа появиться значок нуля или полюса.

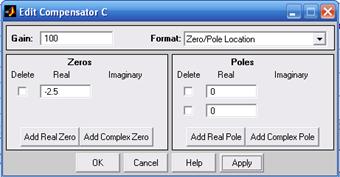
Рис. 8.3. Задание параметров передаточной функции

Таким образом, определяя показатели качества (перерегулирование) в функции коэффициента усиления, можно выбрать значения K оптимизирующее переходной процесс для заданной структуры.

В Simulink Extras в разделе Additional Linear находятся два блока PID controller (ПИД-регулятор). В одном из них выходной сигнал задается выражением

OUT = P + I/s + D×s,

где P, I, D – это настроечные параметры, изменяя которые можно задавать различные типы регуляторов, в том числе делать из ПИД-регулятора П-регулятор, ПИ-регулятор и ПD-регулятор.

Операция дифференцирования в этом блоке выполняется довольно грубо.

В блоке PID controller with Approximate Derivative (ПИД-регулятор с улучшенной операцией дифференцирования) операция дифференцирования за счет параметра N выполняется точнее

OUT = P + I/s + D×s/(N×s + 1)

Описание работы

Желаемая передаточная функция W_Ж(s) разомкнутой, настроенной на симметричный оптимум системы, имеющей максимальный запас устойчивости по фазе, с объектом регулирования в виде апериодического звена имеет вид:

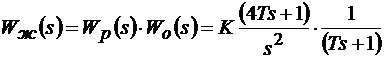, (8.1)

где K – коэффициент усиления разомкнутой системы, T – постоянная времени объекта, представляющего собой апериодическое звено.

Параметры блоков SISO Model:

T01=0.1; %Постоянная времени объекта

G1=tf(1,[T01,1]) %Передаточная функция объекта

C1=tf([4*T01,1],[1,0,0]) %Передаточная функция регулятора

H1=tf(1,[0.005,1]) %Передаточная функция обратной связи

F1=tf(1,1) %Передаточная функция фильтра

Sisotool.

На рис. 8.4 изображены корневые годографы и логарифмические частотные характеристики объекта, полученные с помощью инструмента SISO Design Tool.

Показатели системы управления исследуют в функции коэффициента усиления K. При коэффициенте усиления равном 1 запас по фазе составляет 16,3° (рис. 8.4а).

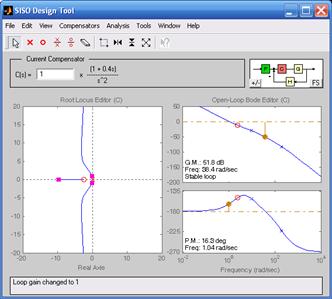
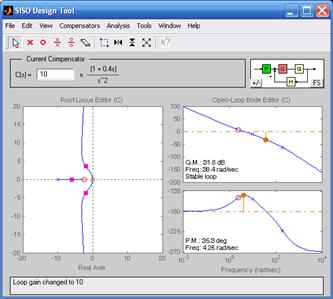
а) б)

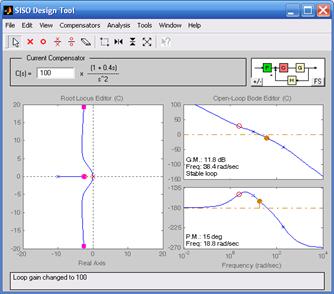
в)

а) K =1; б) K = 10;в) K = 100

Рис. 8.4. Корневой годограф и частотные характеристики исследуемой системы

Качество переходного процесса анализируют по переходной характеристике (меню Analysis, подменю Response to Step Command) (рис. 8.5).

Переходный процесс при K = 1 имеет неудовлетворительный характер (большое перерегулирование – 66% и значительную колебательность). Измененный коэффициент усиления K можно внести в окно Current Compensation и зафиксировать его с помощью щелчка курсором джойстика в поле корневого годографа. При увеличении коэффициента усиления полюса смещаются влево от мнимой оси, что улучшает качество переходного процесса. Об этом свидетельствуют и логарифмические характеристики – увеличивается частота среза системы, что приводит к увеличению быстродействия, увеличению запаса по фазе и уменьшению перерегулирования. Переходная характеристика на рис. 8.5б при K = 10 подтверждает проведенный анализ по частотным характеристикам и корневому годографу.

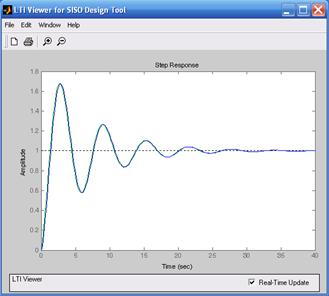
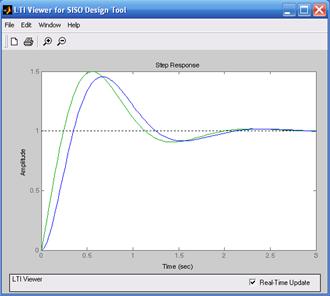
а) б)

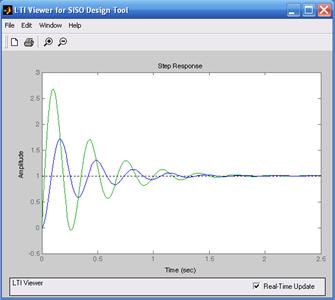
в)

Рис. 8.5. Переходные функции исследуемой системы: а) K =1; б) K = 10;в) K = 100

Дальнейшее исследование системы регулирования идет с помощью изменения параметров регулятора и структурной схемы. Например, можно при выбранном K ввести в систему фильтр. Для этого следует войти в меню File, подменю Import и ввести передаточную функцию фильтра в структурную схему (рис. 8.2). Исследуемая структура (рис. 8.1) позволяет оценить изменение параметров обратной связи, например, вводя в обратную связь апериодическое звено. Для этого параметры фильтра и апериодического звена должны быть предварительно определены в m-файле и при его выполнении занесены в Workspace.

Для объекта, являющегося апериодическим звеном второго порядка необходимо предварительно записать в Workspace передаточные функции объекта W_o(s) и регулятора W_р(s). Передаточная функция объекта является произведением передаточных функций апериодических звеньев

,

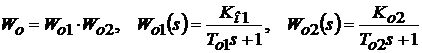где K_o1, K_o2- коэффициенты усиления апериодических звеньев;

Т_o1, Т_o2 - постоянные времени апериодических звеньев.

Передаточная функция объекта при его настройке на симметричный оптимум имеет желаемую передаточную функцию

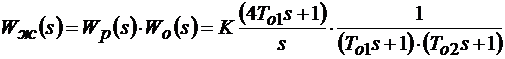. (8.2)

При настройке системы на технический оптимум

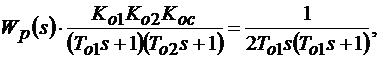(8.3)

где K_ос – коэффициент усиления звена обратной связи.

Из соотношения (8.3) получаем, что в систему должен быть включен пропорционально-интегральный регулятор (ПИ-регулятор) с параметрами

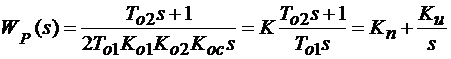(8.4)

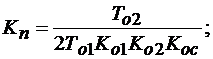
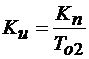; (8.5)

Структура данной системы регулирования изображена на рис.8.6.

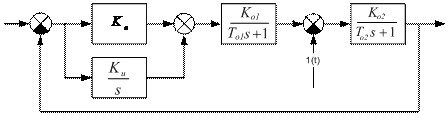
Рис. 8.6. Настройка на технический оптимум

Далее, с использованием команд sisotool, выполнены исследования аналогичные тем, которые применялись к передаточной функции (8.1).

T01=0.01; %Постоянная времени первого звена

T02=0.1; %Постоянная времени второго звена

K01=1; %Коэффициент усиления первого звена

K02=1; %Коэффициент усиления второго звена

Kos=1; %Коэффициент усиления звена обратной связи

Kp=T02/2/T01/K01/K02/Kos %Коэффициент усиления П-регулятора

Ki=Kp/T02 %Коэффициент усиления И-регулятора

G1=tf(1,[T01*T02,T01+T02,1]) %Передаточная функция объекта

C1=tf([4*T01,1],[1,0]) %Передаточная функция регулятора 1

C2=tf([Kp,Ki],[1,0]) %Передаточная функция регулятора 2

H1=tf(1,1) %Передаточная функция звена обратной связи

F1=tf(1,1) %Передаточная функция фильтра

Sisotool.

На рис. 8.7 изображены корневые годографы и логарифмические частотные характеристики объекта для случая симметричного оптимума (рис. 8.7а) и технического оптимума (рис. 8.7б).

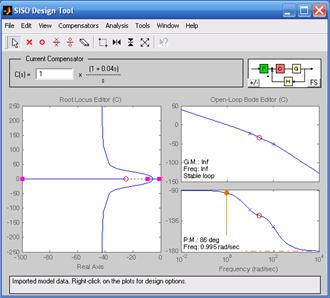
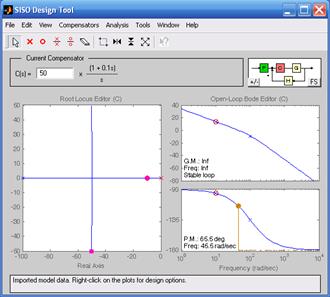
а) б)

Рис. 8.7. Годографы и частотные характеристики апериодического звена второго порядка

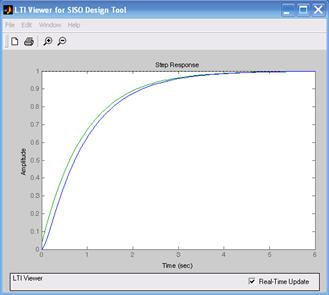
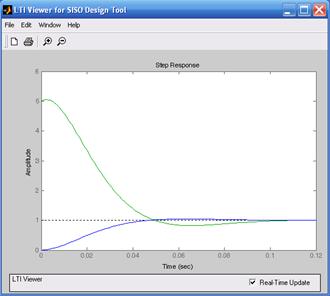
На рис. 8.8 изображены переходные характеристики объекта для случая симметричного оптимума (рис. 8.8а) и технического оптимума (рис. 8.8б).

Для объекта, состоящего из трех последовательно соединенных апериодических звеньев, технический оптимум определяется соотношением

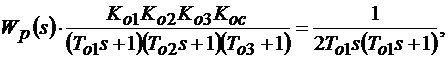(8.6)

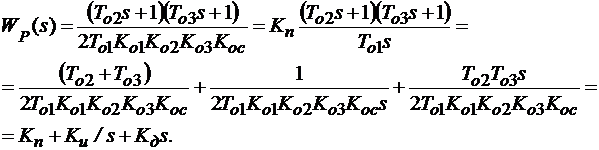(8.7)

Структура данной системы регулирования изображена на рис.8.9.

а) б)

Рис. 8.8. Переходные характеристики апериодического звена второго порядка

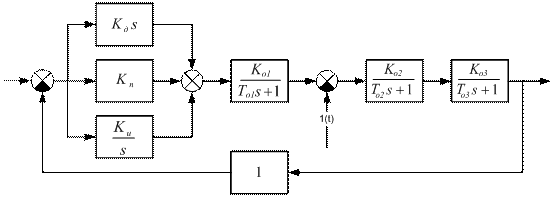
Рис. 8.9. Переходные характеристики апериодического звена второго порядка

T01=0.01; %Постоянная времени первого звена

T02=0.1; %Постоянная времени второго звена

T03=0.2; %Постоянная времени третьего звена

K01=1; %Коэффициент усиления первого звена

K02=1; %Коэффициент усиления второго звена

K03=1; %Коэффициент усиления третьего звена

Kos=1; %Коэффициент усиления звена обратной связи

Kp=(T02+T03)/2/T01/K01/K02/K03/Kos %Коэффициент усиления П-регулятора

Ki=Kp/(T02+T03) %Коэффициент усиления И-регулятора

Kd=Ki*T02*T03 %Коэффициент усиления Д-регулятора

G1=tf(1,[T01*T02*T03,(T01*T02+T01*T03+T02*T03),(T01+T02+T03),1]) %Передаточная функция объекта

C1=tf([Kd,Kp,Ki],[1,0]) %Передаточная функция регулятора

H1=tf(1,1) %Передаточная функция звена обратной связи

F1=tf(1,1) %Передаточная функция фильтра

Sisotool

На рис. 8.10а изображен годограф и частотные характеристики объекта, на рис. 8.10б изображены переходные характеристики системы регулирования.

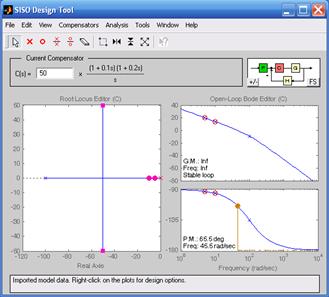
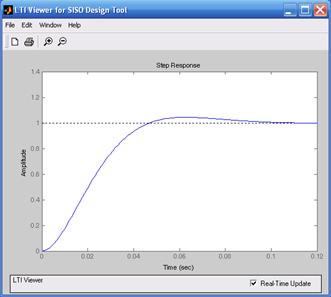
а) б)

Рис. 8.10. Годограф, частотные и переходные характеристики объекта

Таким образом, если объект регулирования апериодическое звено второго порядка, то для настройки системы на технический оптимум следует применить ПИ-регулятор, а если объект регулирования представляет три последовательно соединенных апериодических звена, то для настройки системы на технический оптимум следует применить ПИД-регулятор.

Задание

1. Для заданной постоянной времени (8.1), используя команду sisotool перенести данные Workspace в блоки, образующие структуру исследуемой системы.

2. Для рассчитанных параметров регулятора определить корневой годограф и логарифмические характеристики как функцию коэффициента усиления.

3. Используя меню Analis, подменю Response to Step, определить переходную функцию.

4. Исследовать качественные показатели системы (величину перерегулирования) как функцию коэффициента усиления.

5. Используя команду sisotool составить структурную схему согласно (8.2), (8.4), рис.8.6 (данные схемы приведены в индивидуальном задании).

6. Повторить пункты 1 – 4.

7. Используя команду sisotool составить структурную схему согласно (8.7), рис. 8.9 (данные схемы приведены в индивидуальном задании).

8. Повторить пункты 1 – 4.

Содержание отчета

1. Расчетные значения параметров регуляторов.

2. Экспериментальные годографы, переходные и частотные характеристики исследуемых систем.

3. Общий анализ систем регулирования, связанный с вариацией параметров системы и регулятора.

4. Анализ качества регулирования в функции коэффициента усиления.

Контрольные вопросы

1. Какую информацию можно получить из корневого годографа?

2. Какие возможности открывает MatLab при использовании команды sisotool?

3. Как поместить данные из рабочего пространства MatLab в блоки, образующие структурную схему, используемую в команде sisotool?

4. Как изменить параметры объекта в команде sisotool?

5. Как изменить параметры регулятора в команде sisotool?

6. Как изменяться выходные сигналы по управлению и возмущению, если на входе системы, настроенной на симметричный оптимум, ввести фильтр?

7. Какое звено передаточной функции системы способствует увеличению перерегулирования?

8. Укажите пути уменьшения перерегулирования в системе, настроенной на симметричный оптимум.

9. В каком разделе MATLAB помещен блок - PID Controller.

10. Изобразите вид переходной функции на выходе ПИ-регулятора.

11. Изобразите вид переходной функции на выходе ПИД-регулятора.

Лабораторная работа № 9