Построение графика линейной функции по данным наблюдения, полученной МНК
График линейной функции, полученной МНК, можно получить с помощью функции lsline. Для этого сначала нужно построить график, соответствующий рядам данных экспериментов (для вывода точек корреляционного поля используются «+», для вывода полученной прямой – «*», системная прямая выведется синей линией), затем воспользоваться этой функцией. Например:
>>plot(x,y,’+’, x, a+b*x,’*’); lsline
Задание.
На один график выведите ряды данных эксперимента, полученную вами прямую и прямую, полученную встроенными средствами MATLAB. Сравните результаты.
Оценка погрешности парной линейной регрессии
После построения модели необходимо выполнить проверку ее адекватности.
Оценка адекватности модели производится на основании анализа значения коэффициента корреляции r, вычисляемого по формуле:
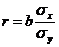 , (2.9)
, (2.9)
где
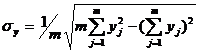 ; (2.10)
; (2.10)
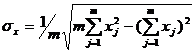 . (2.11)
. (2.11)
Его величина может изменяться в пределах отрезка от –1 до 1. Чем ближе к единице модуль значения коэффициента корреляции, тем теснее линейная связь между х и у. При полном отсутствии связи r = 0, при |r|<0.5 гипотеза о наличии линейной связи отвергается, и линейная модель признается неадекватной.
Что касается диапазона значений модуля коэффициента от 0.5 до 1, то минимальный предел значения модуля r, при котором модель признается адекватной, определяется требованиями к точности модели – чем выше требования, тем ближе этот предел к единице.
Помимо оценки тесноты связи, коэффициент корреляции позволяет судить о характере зависимости между величинами х и у: если r > 0, между х и уимеет место положительная корреляционная связь, т. е. с ростом параметра х увеличивается параметр у; если r < 0, между х и у имеет место отрицательная связь.
Мерой ошибки регрессионной модели служит среднее квадратичное отклонение (стандартное отклонение), которое рассчитывается по формуле:
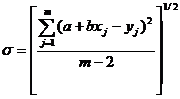 . (2.12)
. (2.12)
Задание. Вычислить значения всех приведенных параметров, оценить достоверность полученных коэффициентов.
Содержание отчета
В отчете должны быть представлены:
– решения задач к п. 1 и п. 2;
– понятие регрессии, суть метода наименьших квадратов;
– последовательность команд для нахождения коэффициентов линейной регрессии и полученные коэффициенты;
– полученное уравнение линейной регрессии;
– график полученной прямой, системной прямой и точек корреляционного поля;
– команды для вычисления коэффициента корреляции, среднего квадратичного отклонения и полученные значения;
– анализ достоверности и точности полученной линейной модели.
ЛАБОРАТОРНАЯ РАБОТА № 3
Тема: НЕЛИНЕЙНАЯ РЕГРЕССИЯ.
ПОДГОНКА КРИВЫХ И ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ
Цель работы. Получение вида и параметров нелиненой зависимости между величинами x по y экспериментальным данным.
Краткие сведения из теории
Связь между аргументом и функцией может иметь нелинейный характер. Аппроксимация кривой выполняется тем же путем с использованием метода наименьших квадратов, что и в случае прямой линии . Линия регрессии должна удовлетворять условию минимума суммы квадратов расстояний до каждой точки корреляционного поля. В данном случае в уравнении (1) упредставляет собой расчетное значение функции, определенное при помощи уравнения выбранной криволинейной связи по фактическим значениям хj.
В общем случае нелинейной зависимости
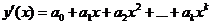 .
.
По методу наименьших квадратов находим частные производные по коэффициентам регрессии и приравниваем их к нулю. Получаем систему уравнений:
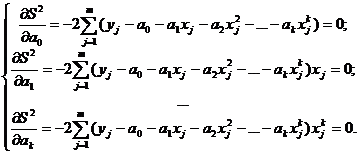
Оценкой тесноты связи при криволинейной зависимости служит теоретическое корреляционное отношение hxу , представляющее собой корень квадратный из соотношения двух дисперсий: среднего квадрата sр2 отклонений расчетных значений y' j функции по найденному уравнению регрессии от среднеарифметического значения Y величины y к среднему квадрату отклонений sy2фактических значений функции yj от ее среднеарифметического значения :
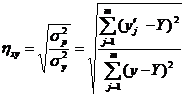 .
.
Порядок выполнения работы.
1 Загрузите ряды данных – вектора x и y.
2 Командой cftool откройте основное окно Curve Fitting Tool.
3 Нажмите кнопку DATA.
4 Задайте XData (вектор х) и YData (вектор y).
5 Нажмите Create data set и OK – окно закроется.
6 Нажмите кнопку Fitting. Появится окно редактора подгонки кривых.
7 Для выполнения нового сеанса подгонки нажмите New Fit.
8 В списке Type of fit выберите вид функции регрессии. Поочередно устанавливайте следующие виды функции регрессии (для выполнения подгонки нажмите APPLY), результаты (вид функции и значения коэффициентов) увидите в окне Results. Зафиксируйте их в отчете.):
– Polynomial – полиномиальная. Поочередно попробуйте линейную, второго, третьего и четвертого порядка;
– Fourier – приближение рядом Фурье;
– Gaussian – приближение кривой гауссиана;
– Power – степенная функция;
– Rational – рациональная функция с выбором числителя и знаменателя;
– Custom equation – функция, задаваемая пользователем. Попробуйте задать следующие функции:
а) y=ax2+bx3+c,
б) y=asin(2x)–bexp(x–3)+cx+d,
в) такую функцию, которая, по вашему мнению, наилучшим образом приближена к экспериментальным данным.
Для добавления нового слагаемого нажмите Add a term.
9 Выберите три наиболее подходящих функции, выпишите их вид и коэффициенты.
10 Вернитесь в командную строку и для каждой функции вычислите значение теоретического корреляционного отношения.
11 Сделайте вывод о наиболее подходящей функции.
3 Варианты исходных данных:
1. (1, 32.1); (1, 29.5); (1, 30.5); (2, 110.9); (2, 110.5); (3, 272.9); (3, 273.1); (3, 273.3); (4, 560.5); (5, 999.1); (5, 996.9); (6, 1627.3); (6, 1629.1); (6, 1630.1); (7, 2482.7); (8, 3597.1); (9, 5004.7); (9, 5006.7); (10, 6741.9); (10, 6743.5).
2. (1, –49.2); (1, –49.0); (1, –50.0); (2, –110.7); (2, –110.3); (3, –210.0); (3, –208.8); (3, –208.0); (4, –349.3); (5, –541.6); (5, –543.2); (6, –799.3); (6, –801.3); (6, –800.9); (7, –1128.2); (8, –1542.7); (9, –2045.4); (9, –2045.8); (10, –2648.9); (10, –2651.9).
3. (1, –7.1); (1, –6.3); (1, –5.3); (2, 32.2); (2, 29.8); (3, 111.5); (3, 111.1); (3, 112.9); (4, 244.8); (5, 442.5); (5, 442.5); (6, 712.8); (6, 713.8); (6, 715.2); (7, 1073.5); (8, 1525.4); (9, 2090.1); (9, 2088.5); (10, 2768.4); (10, 2768.6).
4. (1, –33.1); (1, –33.3); (1, –32.5); (2, –103.4); (2, –104.4); (3, –215.9); (3, –212.7); (3, –215.1); (4, –364.6); (5, –551.9); (5, –552.7); (6, –779.4); (6, –780.6); (6, –781.6); (7, –1047.5); (8, –1353.8); (9, –1696.1); (9, –1695.5); (10, –2078.4); (10, –2081.2).
5. (1, –2.6); (1, –3.0); (1, –4.6); (2, –49.0); (2, –50.4); (3, –132.0); (3, –132.6); (3, –132.0); (4, –262.0); (5, –445.6); (5, –445.6); (6, –696.2); (6, –696.6); (6, –698.6); (7, –1025.0); (8, –1438.4); (9, –1946.0); (9, –1944.6); (10, –2554.6); (10, –2554.4).
6. (1, 1.7); (1, 3.3); (1, 2.7); (2, –54.9); (2, –53.9); (3, –216.3); (3, –216.9); (3, –216.7); (4, –525.3); (5, –1017.1); (5, –1017.1); (6, –1730.5); (6, –1729.7); (6, –1730.5); (7, –2710.9); (8, –3993.7); (9, –5619.3); (9, –5618.5); (10, –7625.7); (10, –7624.5).
Содержание отчета
Отчет должен содержать:
– общий вид функции нелинейной регрессии, метод получения значений ее коэффициентов;
– вид и коэффициенты трех наиболее подходящих функций, их графики;
– последовательность команд для получения значения теоретического корреляционного отношения для каждой из трех функций и полученные значения;
– выводы на основе анализа полученных значений теоретического корреляционного отношения.
ЛАБОРАТОРНАЯ РАБОТА № 4
