Разработка алгоритмов управления
А.С.Каракулов
Разработка алгоритмов управления
Для микропроцессорных электроприводов.
Лабораторный практикум
Рекомендовано к печати
Редакционно-издательским советом
Томского политехнического университета
Издательство
Томского политехнического университета
Томск 2009
УДК 68-83-52
ББК 3859
К31
Каракулов А.С.
К31 Разработка алгоритмов управления для микропроцессорных электроприводов. Лабораторный практикум: учебное пособие / А.С.Каракулов. – Томск: Издательство Томского политехнического университета, 2009. – 104 с.
В учебном пособии рассмотрены основные методы создания управляющего программного обеспечения для встроенных систем электроприводов. Рассматриваются алгоритмы реализации цифровых регуляторов, логических систем управления, а также специализированных процедур, применяемых в электроприводе.
Предназначено для студентов, обучающихся по специальности 140604 – «Электропривод и автоматика промышленных установок и технологических комплексов», и магистров, обучающихся по магистерской программе 140611 – «Электроприводы и системы управления электроприводов» направления подготовки 140600 – «Электротехника, электромеханика и электротехнологии».
УДК 68-83-52
ББК3859
Рекомендовано к печати Редакционно-издательским советом
Томского политехнического университета
Рецензенты
Кандидат технических наук,
руководитель сектора разработки электромеханических устройств
ООО «Элетим»
С.В.Рикконен
Кандидат технических наук, доцент
Северской государственной технологической академии
С.Н. Кладиев
© Каракулов А.С., 2009
© Томский политехнический университет, 2009
© Оформление. Издательство Томского
политехнического университета, 2009
Введение
Целью практикума является обучение следующему:
1. Использовать среды моделирования Симулинк для моделирования процессов.
2. Использовать готовые компоненты среды Симулинк для создания моделей.
3. Создавать собственные компоненты среды Симулинка для реализации моделей, отсутствующих в Симулинке.
4. Разрабатывать приложение управления процессом моделирования.
5. Разработка структур логического управления электроприводами.
6. Разработка элементарных цифровых регуляторов.
Выполнение заданий по практикуму требует элементарных знаний по программированию, теории электропривода и теории автоматического регулирования.
Практикум содержит 7 занятий. Результатом работы по каждому занятию должен быть отчет. В отчете должны быть приведены результаты моделирования, доказывающие наличие выполненных заданий для самостоятельной работы, а также используемые коды, необходимые для самостоятельно проведенного моделирования.
Примечание
1. При повторном запуске модели Симулинка, необходимо заново перетранслировать S-функцию посредстом нажатия кнопки Build в окне S-function builder для задания нулевых начальных условий модели. Если применяются несколько компонентов S-функций, необходимо перетранслировать заново каждый перед началом каждого моделирования.
2. float static используется для задания имени новой переменной, применяемой в модели.
При генерации S-функции установите дискретный характер вычислений компонента, период дискретизации 0.001 секунда.
Результаты моделирования показаны на рис.1.
Рис.1.
Повторим моделирование с увеличенным напряжением (рис.2.):
Рис.2
Как можно видеть, при увеличении входного сигнала происходит соответствующее увеличение выходного сигнала, форма выходного сигнала одинакова и соответствует реальному поведению тока в RL-цепочке.
Для регулирования тока можно применить простейший цифровой регулятор, который работает по принципу: если выходной сигнал меньше заданного, то увеличиваем напряжение, если больше – то уменьшаем.
В классической теории автоматического управления принято управлять по ошибке (рассогласованию между входной и выходной координатами). С учетом этого, указанный принцип несколько модифицируется:
если ошибка по току меньше нуля, то уменьшаем текущее напряжение на определенное значение, если больше – то увеличиваем.
Для реализации регулятора создадим S-функцию reg, содержимое которой представлено ниже.
float static input=0;
float static output=0;
input=u0[0];
if (input<0) output=output-0.01;
if (input>0) output=output+0.01;
y0[0]=output;
Создадим систему управления током RL-цепочки с использованием этих разработанных S-функций. Модель системы управления показана на рис.3. Как можно видеть, для регулирования используется сигнал обратной связи по току, который вычитается из заданного сигнала. При этом в обратной связи применен компонент Z-1, который обеспечивает задержку в передаче выходного сигнала на сумматор на одну дискрету, то есть на сумматор подается значение, которое было рассчитано при предыдущем шаге расчета.
Задание для самостоятельной работы
В показанной модели установите время моделирования inf (бесконечность), запустите моделирование, и изменяя задания на ток, наблюдайте его изменение в модели RL-цепочки.
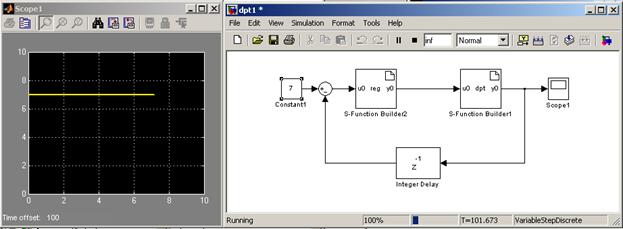
Рис.3
Перейдем теперь к разработке цифровой системы управления двигателем постоянного тока. За основу возьмем двигатель 2ПБ132МГ со следующими характеристиками:
Номинальная мощность 
.
Номинальное напряжение 
.
Сопротивление якорной цепи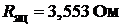 
.
Индуктивность якорной цепи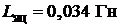 
.
Момент инерции двигателя 
.
Коэффициент ЭДС при номинальном потоке возбуждения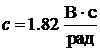 
.
Изначально необходимо создать модель двигателя.
ДПТ может быть описан дифференциальными уравнениями
,
,
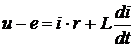где 
– напряжение на якоре, В;
– активное сопротивление, Ом; индуктивность якорной цепи, Гн;
– угловая скорость вращения двигателя, 
;
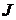– момент инерции якоря двигателя;
– ЭДС двигателя, В;
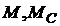– момент двигателя и статической нагрузки, 
;
Момент и ЭДС двигателя определяются по выражениям:
;
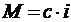Задание для самостоятельной работы
Преобразуйте дифференциальные уравнения, описывающие поведение двигателя постоянного тока в конечно-разностную форму и предложите формулу для расчета тока и скорости двигателя.
Реализация модели двигателя постоянного тока с помощью S-функции может быть выполнена следующим образом:
float static R=3.6;
float static L=0.034;
float static i=0;
float static u=0;
float static t=0;
float static dt=0.001;
float static w=0;
float static Mc=0;
float static Me=0;
float static c=1.82;
float static J=0.038+0.0;
u=u0[0];// забираем входной сигнал - напряжение
Mc=u1[0];
t=t+dt; // расчитываем текущее время
i=i+(u-R*i-c*w)/L*dt; // расчитываем ток
Me=i*c;
w=w+(Me-Mc)/J*dt;
y0[0]=i;// выдача результата
y1[0]=w;
Для регулирования скорости применим тот же самый регулятор, который был разработан для RL-цепочки. С учетом ограничения на максимальное напряжение, которое можно приложить к двигателю, введем программное ограничение на выходное значение регулятора. Текст программы такого регулятора с ограничением выходного значения показан ниже:
float static input=0;
float static output=0;
input=u0[0];
if (input<0) output=output-0.01;
if (input>0) output=output+0.01;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Задание для самостоятельной работы
Соберите модель, показанную на рис.4., установите время моделирования 10 секунд и смоделируйте пуск двигателя при различных заданиях на скорость (компонент Constatnt) и заданиях на момент (компонент Constant2).
Рис.4.
Как можно увидеть при выполнении задания, двигатель выходит на заданную скорость при задании различных моментов, то есть система астатична, что объясняется интегрирующими свойствами примененного регулятора. Недостатком данного регулятора является низкое быстродействие – время выхода на заданную скорость составляет порядка 10 секунд (см.рис.4).
Задание для самостоятельной работы
Предложите свой способ увеличения быстродействия системы.
Применим пропорциональный регулятор с коэффициентом усиления 10. Для этого содержимое S-функции регулятора должно принять следующий вид:
float static input=0;
float static output=0;
input=u0[0];
output=10*input;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Установите время моделирования 0,2 секунды. В результате должны получиться графики переходных процессов, идентичные представленным на рис.5. Как видно из графиков, установившаяся скорость отличается от заданной (42 против 50). При увеличении нагрузки (рис.6) различие увеличивается. Данный пример демонстрирует отсутствие астатизма П-регулятора.
Задание для самостоятельной работы
Предложите способ уменьшения ошибки регулирования при применении П-регулятора.
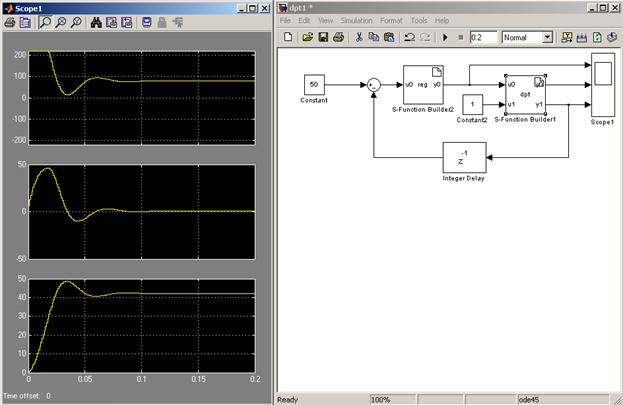
Рис.5
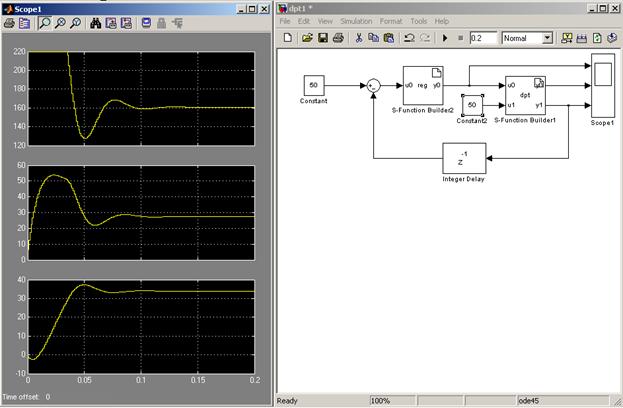
Рис.6
Еще одним простейшим регулятором является релейный. Его реализация будет выглядеть следующим образом:
float static input=0;
float static output=0;
input=u0[0];
if (input<0) output=-220;
if (input>=0) output=220;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Релейный регулятор характеризуется резкими переключениями при регулировании, что ведет к колебательности процессов при срабатываний регулятора (см.рис.7).
Задание для самостоятельной работы
1. Упростите предложенный регулятор.
2. Изменяя задание на скорость и момент нагрузки, определите, является ли релейный регулятор астатичным.
3. Предложите способы устранения колебаний координат управляемой системы, возникаемых при работе релейного регулятора.
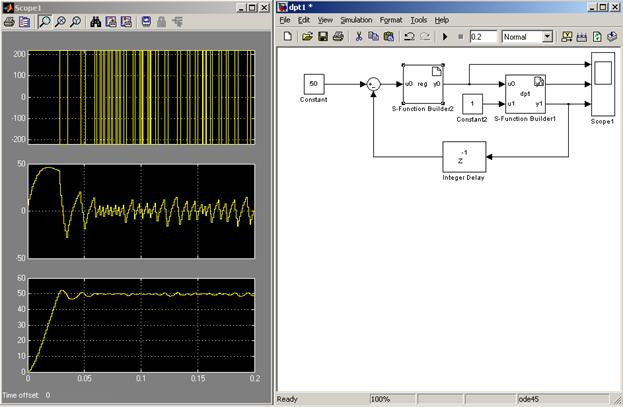
Рис.7
Одним из способов устранения недостатков работы релейного регулятора является введение зоны гистерезиса. Реализация такого регулятора будет следующей (ширина гистерезиса – от -3 до 3):
float static input=0;
float static output=0;
input=u0[0];
if (input<-3) output=-220;
if (input>3) output=220;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Результат работы такого регулятора показан на рис.8.
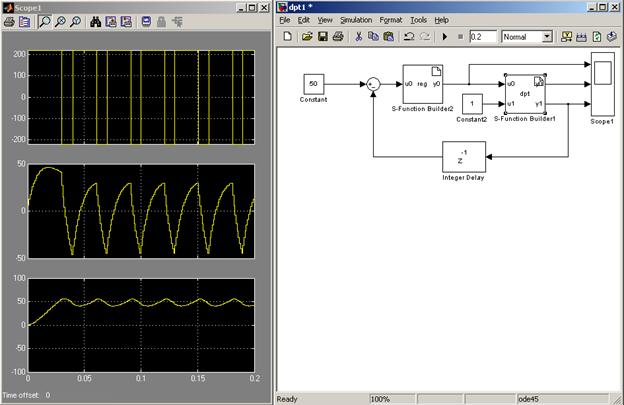
Рис.8
На практике очень распространен ПИ-регулятор.
Передаточная функция непрерывного ПИ-регулятора, реализуемого на аналоговой технике (например, на базе операционных усилителей), имеет вид:
,
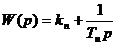где 
– коэффициент передачи пропорциональной части,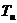 
– постоянная интегрирования. Если обозначить входной сигнал, который обычно является величиной рассогласования между заданным значением регулируемой величины и ее фактическим значением, снимаемым с датчика обратной связи, как 
, а выходное управляющее воздействие, подаваемое на вход объекта управления, как 
, то передаточной функции ПИ-регулятора будет соответствовать дифференциальное уравнение:
.
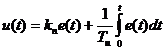Продифференцируем исходное уравнение непрерывного ПИ-регулятора, чтобы избавиться от интеграла:
.
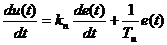Для перехода от непрерывного уравнения к разностному заменим непрерывные переменные дискретными, дифференциалы этих переменных – разностями, а приращение времени 
– величиной интервала квантования по времени T. Получим:
.
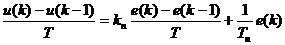После очевидных алгебраических преобразований разностное уравнение ПИ-регулятора примет вид:
.
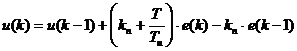Обозначим коэффициенты:
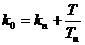и 
.
С учетом полученных коэффициентов уравнение будет выглядеть следующим образом:
.
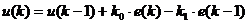На рис.9 представлена структурная схема ПИ-регулятора с неявновыраженной интегральной составляющей и общим ограничением, где Звено 
— запаздывание на такт.
Рис.9
Реализация ПИ-регулятора в Симулинке выглядит следующим образом:
float static input=0;
float static output=0;
float static k0=2+0.001/0.01;
float static k1=2;
float static input_prev=0;
input=u0[0];
output=output+k0*input-k1*input_prev;
input_prev=input;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Как видно из рис.10 и 11, при работе ПИ-регулятора ошибка регулирования для установившегося значения, в отличии от П-регулятора, равна практически нулевому значению при различных моментах сопротивления нагрузки.
Рис.10
Рис.11
Задание для самостоятельной работы
Введите контур тока в рассматриваемую модель и реализуйте его на базе ПИД-регулятора.
Лабораторный практикум
Учебное пособие
Научный редактор
доктор технических наук,
профессор Р.Ф.Бекишев
Редактор И.О. Фамилия
Верстка И.О. Фамилия
Дизайн обложки И.О. Фамилия
| Подписано к печати . .2008. Формат 60х84/16. Бумага «Снегурочка». Печать Xerox. Усл. печ. л. 000. Уч.-изд. л. 000. Заказ ХХХ. Тираж ХХХ экз. | |||||
 | Томский политехнический университет Система менеджмента качества Томского политехнического университета сертифицирована NATIONAL QUALITY ASSURANCE по стандарту ISO 9001:2000 |  | |||
 . 634050, г. Томск, пр. Ленина, 30. | |||||
 |
А.С.Каракулов
Разработка алгоритмов управления