Показатели тесноты связи факторов с результатом.

Если факторные признаки различны по своей сущно­сти и/или имеют различные единицы измерения, то коэф­фициенты регрессии 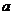при разных факторах являются не­сопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с ре­зультатом, позволяющими ранжировать факторы. К ним от­носят: частные коэффициенты эластичности, β-коэффициенты, частные коэффициенты корреляции.

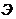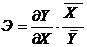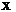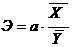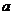Частные коэффициенты эластичности рассчитываются по формуле: . Частный коэффициент эластичности показывают на сколько процентов в среднем изменяется признак-результат Y с изменением признака-фактора на один процент от своего среднего уров­ня при фиксированном положении других факторов модели. В случае линейной зависимости коэффициент эластичности рассчитывается по формуле: , где - коэффициент регрессии .

Стандартизированные частные коэффициенты регрессии - β-коэффициенты 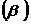показывают, на какую часть своего среднего квадратического отклонения 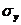изменится признак-результат Y с изменением соответствующего фак­тора 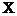на величину своего среднего квадратического от­клонения 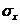при неизменном влиянии прочих факторов входящих в уравнение.

По коэффициентам эластичности и β-коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разно­направленное воздействие факторов на результат.

Кроме того, коэффициент 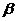может интерпретировать­ся как показатель прямого (непосредственного) влияния фактора 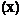на результат 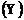. Во множественной регрес­сии фактор оказывает не только прямое, но и косвен­ное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели). Косвенное влияние измеря­ется величиной: 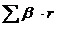,где т- число факторов в модели. Полное влияние фактора на результат равное сумме прямого и косвенного влияний измеряет коэффици­ент линейной парной корреляции данного фактора и ре­зультата – .

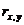Коэффициент частной корреляцииизмеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели.

Для качественной оценки тесноты связи можно использовать следующую классификацию:

0.1- 0.3- слабая связь

0.3-0.5 – умеренная связь

0.5-0.7- заметная связь

0.7-0.9- тесная связь

0.9-0.99- весьма тесная

Для расчета частных коэффициентов корреляции мо­гут быть использованы парные коэффициенты корреляции.

Для случая зависимости Yот двух факторов можно вычислить 2 коэффициента частной корреляции:

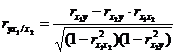(2-ой фактор 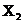фиксирован).

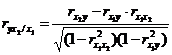(1-ый фактор 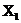фиксирован).

Это коэффициенты частной корреляции 1-ого порядка (порядок определяется числом факторов, влияние которых на результат устраняется).

Частные коэффициенты корреляции, рассчитанные по таким формулам, изменяются от -1 до +1. Они используют­ся не только для ранжирования факторов модели по степени влияния на результат, но и также для отсева факторов. При малых значениях 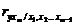нет смысла вводить в уравнение m-ый фактор, т.к. качество уравнения регрессии при его введении возрастет незначительно (т.е. теоретиче­ский коэффициент детерминации увеличится незначительно).

Коэффициенты множественной детерминации и корреляции характеризуют совместное влияние всех факторов на результат.

По аналогии с парной регрессией можно определить долю вариации результата, объясненной вариацией вклю­ченных в модель факторов 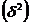, в его общей вариации 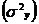. Ее количественная характеристика - теоретический множественный коэффициент детерминации 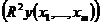. Для линейного уравнения регрессии данный показатель может быть рассчитан через β-коэффициенты, как:

.

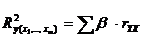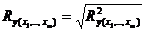- коэффициент множественной корреляции. Он принимает значения от 0 до 1 (в отличие от парного коэффициента корреляции, который может принимать отрицательные значения, R используется без учета на­правления связи). Чем плотнее фактические значения 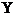располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина 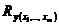. Таким образом, при значении R близком к 1, урав­нение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат; при значении R близком к 0 уравнение регрессии плохо описывает фактиче­ские данные и факторы оказывают слабое воздействие на результат.

Оценка значимости полученного уравнения множест­венной регрессии.

Оценка значимости уравнения множественной регрес­сии осуществляется путем проверки гипотезы: 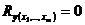(гипотеза о незначимости уравнения регрессии).

Для ее проверки используют F-критерий Фишера.

При этом вычисляют фактическое (наблюдаемое) зна­чение F-критерия:

,

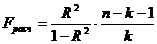где n-число наблюдений; k - число независимых переменных модели.

По таблицам распределения Фишера находят критическое значение F-критерия 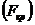. Для этого за­даются уровнем значимости 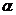(обычно его берут равным 0,05) и двумя числами степеней свободы 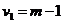и 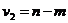. Здесь m – число параметров модели.

Сравнивают фактическое значение F-критерия 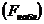с табличным 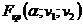. Если 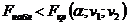, то гипотезу о незначимости уравнения регрессии не отвергают. Если 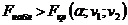, то выдвинутую гипотезу отвер­гают и принимают альтернативную гипотезу о статистиче­ской значимости уравнения регрессии.

Пример 2.

На основе данных, приведенных в Приложении и соответст­вующих варианту 100, требуется:

1. Построить уравнение множественной регрессии. Для этого, ос­тавив признак-результат тем же выбрать несколько признаков-факторов из приложения 1 (границы их наблюдения должны совпадать с границами наблюдения признака-результата, соот­ветствующих Вашему варианту). При выборе факторов нужно руководствоваться как экономическим содержанием, так и формальными подходами (например, матрица парных коэффи­циентов корреляции). Пояснить смысл параметров уравнения.

2. Рассчитать частные коэффициенты эластичности.

3. Определить стандартизованные коэффициенты регрессии (β-коэффициенты).

4. На основе полученных результатов сделать вывод о силе связи результата с каждым из факторов.

5. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.

6. Дать оценку полученного уравнения с помощью общего F-критерия Фишера.

Решение:

По условию задачи, результативный признак должен остаться тот же, значит Y - дивиденды, начисленные по результатам деятельности.В качестве факторных признаков выберем следующие:

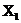– балансовая прибыль;

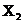- дебиторская задолженность по результатам деятельности.

Определим уравнение регрессии следующего вида:

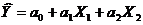
Для определения параметров уравнения связи, а также для дальнейших расчетов построим дополнительную таблицу. (Таблица 2)

Для определения параметров двухфакторного уравнения регрессии необходимо решить систему нормальных уравнений:

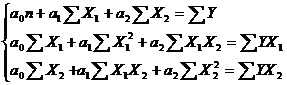
В нашем случае система нормальных уравнений примет вид:

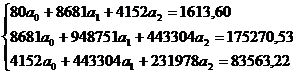
В результате решения данной системы получим следующие коэффициенты регрессии:

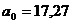
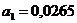
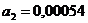
Окончательное уравнение регрессии примет вид:

.

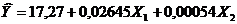При отсутствии влияния со стороны факторных признаков, учтенных в данной модели, значение результативного признака будет составлять 17,2714 млн. руб. При изменении балансовой прибыли на 1 млн. руб. произойдет изменение начисленных дивидендов в ту же сторону на 0,02645 млн. руб., а при изменении дебиторской задолженности на 1 млн. руб. следует ожидать изменения величины начисленных дивидендов на 0,00054 млн. руб.

Определим частные коэффициенты эластичности:

,

.

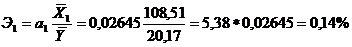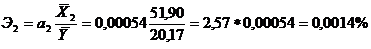Частные коэффициенты эластичности показывают влияние отдельных факторов на результативный показатель. Так, при изменении балансовой прибыли на 1% при неизменности второго фактора произойдет в среднем изменение величины начисленных дивидендов на 0,14%, а при изменении дебиторской задолженности на 1% при фиксированном положении первого фактора произойдет изменение величины начисленных дивидендов в среднем на 0,0014%.

Теперь рассчитаем β-коэффициенты:

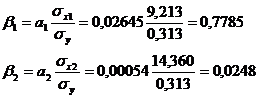
Анализ β-коэффициентов показывает, что на величину начисленных дивидендов из двух исследуемых факторов с учетом уровня их вариации большее влияние оказывает балансовая прибыль .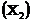

С учетом всех рассчитанных показателей и параметров уравнения регрессии можно сделать вывод о том, что наибольшая связь величины начисленных дивидендов отмечается с размером балансовой прибыли.

Далее, определим парные, частные коэффициенты корреляции и множественный коэффициент корреляции.

I. Парные коэффициенты корреляции: измеряют тесноту связи между двумя из рассматриваемых признаков.

,

,

.

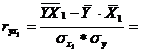
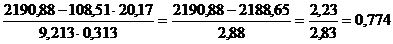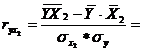
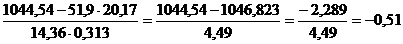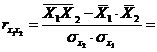
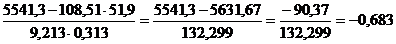Коэффициент корреляции между факторными признаками, равный -0,683, позволяет оставить в модели оба фактора, так как связь между факторами не тесная .

II. Частные коэффициенты корреляции: характеризуют степень влияния одного из факторов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне.

= ,

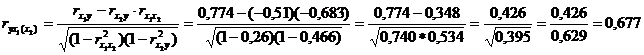
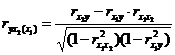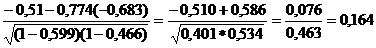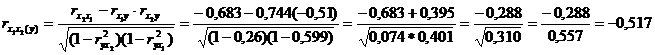
Таблица 2 - Дополнительная таблица

Близкая к тесной прямая связь результативного признака наблюдается с балансовой прибылью (0,677), практически отсутствует связь между начисленными дивидендами и дебиторской задолженностью (0,164).

III. Множественный коэффициент корреляции: показывает тесноту связи между результативным и обоими факторными признаками.

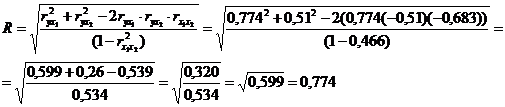
Таким образом, выявлена тесная связь 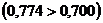между начисленными дивидендами и следующими признаками: балансовая прибыль и дебиторская задолженность.

Множественный коэффициент детерминации определим как квадрат множественного коэффициента корреляции:

.

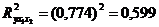На основе коэффициента детерминации делаем вывод, что на 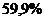вариации величины начисленных дивидендов находится в зависимости от изменения балансовой прибыли и суммы дебиторской задолженности, и на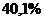 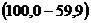– влиянием прочих неучтенных в модели факторов.

На завершительном этапе анализа проверим значимость параметров уравнения регрессии и модели в целом.

Проверим значимость модели в целом с помощью F-статистики Фишера. Для этого определим остаточную дисперсию результативного признака:

,

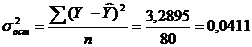Тогда

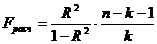= 57,51

,

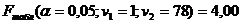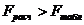, следовательно, модель в целом признается значимой.