Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

Коэффициент эластичности является показателем силы связи, выраженным в процентах. То есть коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения. При линейной связи признаков х и у среднего коэффициента эластичности в целом по совокупности определяется как:

В нашем случае коэффициент эластичности равен:

Эу/х=0, 39*(695,1764706/394,5294118)

При вычислении на ЭВМ получаем следующее значение: 0,686341882

В среднем по совокупности результативный показатель у изменится на 68,6% при изменении фактора х на 1%.

Оцените с помощью средней ошибки аппроксимации качество уравнений.

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е.Y и 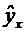Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

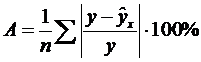
Существует и другая формула определения средней ошибки аппроксимации:

где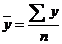

Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе модели к исходным данным.

В нашем примере ошибка аппроксимации равна:16, 9%

В данном случае ошибка аппроксимации больше допустимой нормы, что свидетельствует о не качественном подборе модели к исходным данным.

Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.

F-критерий Фишераиспользуется для оценки значимости уравнения регрессии. Для этого выполняется сравнение фактического F_факг и критического (табличного) F_табл зна­чений F-критерия Фишера. F_факт определяется из соотношения зна­чений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

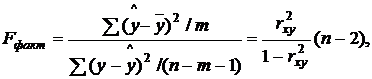
где п — число единиц совокупности;

m - число параметров при переменных x..

F_табл - это максимально возможное значение критерия под влия­нием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть пра­вильную гипотезу при условии, что она верна. Обычно а принимает­ся равной 0,05 или 0,01.

Если F_табл < F_факг, то H_о - гипотеза о случайной природе оцени­ваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F_табл > F_факг, то гипотеза H_о не от­клоняется и признается статистическая не значимость, ненадежность y уравнения регрессии.

Получим: F_{факт =} 0,345954/(1-0,345954)*15=7,9

Можно сделать вывод, что нулевая гипотеза неверна, уравнение считается значимым.

7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости =0,05.

Прогнозное значение y_p определяется путем подстановки в урав­нение регрессии 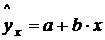соответствующего (прогнозного) зна­чения Х_р. Вычисляется средняя стандартная ошибка прогноза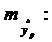

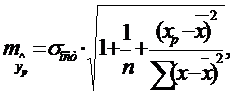
где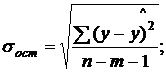

и строится доверительный интервал прогноза:

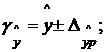
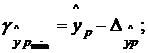
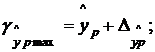
где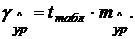

Вычислим прогнозное значение Упр, при условии что Хпр увеличится на 10%.

Xp=695,17*1.1=764,69

Yp=123,74+0.389*764.69=421,6