Алгоритм решения задачи множественной регрессии

1. Определить матрицу r из соотношения:

r = (X T ⋅ X )−1 ⋅(X T ⋅Y ).

2. Для оценки значимости модельной функции вычислить наблюдаемое зна-

чение критерия Фишера

Fнабл. =

Sфакт.

⋅(n− p −1)

⋅

, где

n

Sобщ.

= ∑ (yi

2

)

− y ,

Sост.

n

= ∑ (yi − yˆi ) ,

i =1

Sфакт.

= Sобщ.

Sост. p

− Sост. .

i =1

По таблице критических точек распределения Фишера (приложение 6) оп-

ределить

Fкр. (α, p, n − p −1), где α – уровень значимости. Если

Fнабл. > Fкр. (α, p, n − p −1), то уравнение регрессии значимо, т.е. его можно

использовать для прогноза в генеральной совокупности, в противном слу-

чае – нельзя.

3. В случае значимости уравнения регрессии оценить значимость коэффициен-

тов регрессии

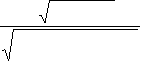
ri , i =1, 2,..., p , используя критерий Стьюдента:

t набл. =

ri n − p −1 ,

s

2

ii

ii

ост.

⋅(X T

⋅ X )−1

s

где

=

2

ост.

Sост.

n − p −1

, (X T ⋅ X )−1 – диагональный элемент матрицы (X T ⋅ X )−1 ,

ri – выборочный коэффициент регрессии,

i =1,

2, ...,

p . Для этого найти

критическое значение критерия по таблице критических точек распреде-

ления Стьюдента

tкр. (α;

n − p −1)

(приложение 3). Если

t набл.

> t кр. (α, n − p −1), то коэффициент ri

значимо отличается от нуля, в

противном случае коэффициент ri

не является значимым.

4. Используя модельное уравнение регрессии, спрогнозировать индивиду-

альные значения результативной переменной при

X 1 = x1 ,

X 2 = x2 , …,

X p = x p . Для этого рассмотреть вектор-столбец

X 0 = (1,

X

x1 ,

p

x2 , ...,

x )T и

найти доверительный интервал для прогнозного значения по формуле:

yˆ 0 −tкр. (α; n − p −1)⋅S y

≤ y0 ≤ yˆ 0 + tкр. (α; n − p −1)⋅S y ,

где

= s

S y 0

⋅

2

ост.

1 + X T

⋅(X T

⋅ X )−1

⋅ X 0 ,

T – вектор-строка.

Задача исследования степени связи между переменными решается с по- мощью корреляционного анализа. Методы корреляционного анализа приме- няются в случае, когда данные, полученные в выборке, можно считать слу- чайными и выбранными из совокупности, распределенной по нормальному закону, поэтому будем предполагать, что эти условия выполнены.

В практических исследованиях о тесноте корреляционной связи между рассматриваемыми одномерными величинами X и Y судят не по величине

генерального коэффициента корреляции r (который обычно неизвестен), а

по величине его выборочного коэффициента корреляции

Определение 12.2. Величина

n

rв .

∑ (xi

− x)(yi

− y )

r= i =1

в

n

n

∑ (xi

− x)2

⋅ ∑ (yi

− y )2

i =1

i =1

называется выборочным(парным) коэффициентом корреляции между X и Y .

Замечание. Выборочный коэффициент корреляции удовлетворяет

двойному неравенству

−1 ≤ rв

≤1. По его величине и знаку можно судить о

тесноте и направлении связи между X и Y .

Для проверки выборочного коэффициента корреляции на значимость,

т.е. гипотезы

H0 : rв = 0 , при конкурирующей гипотезе

H1 : rв ≠ 0 , нужно вы-

числить наблюдаемое значение t -критерия по формуле:

1 − r2

набл.

t = rв n − 2 .

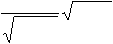
в

Гипотеза

H 0 принимается, если

tнабл.

<tкр. (α; n − 2)

(находится по таблице

приложения 3), и отвергается, если

t набл.

≥ t кр. . Если гипотеза

H0 будет от-

вергнута, то можно сделать вывод о значимости (достоверности) выборочно-

го коэффициента корреляции

rв . Иначе говоря, между признаками X и Y в

генеральной совокупности существует корреляционная связь.

Рассмотрим теперь многомерные модели. Пусть имеется совокупность

переменных

X1 ,

X 2 , …,

X p , имеющих совместное нормальное распределе-

ние. Оценкой неизвестной генеральной корреляционной матрицы является

матрица выборочных коэффициентов корреляции

rij :

⎛ 1 r12

⎜

...

r1 p ⎞

⎟

⎜r21

Rв =⎜ ...

⎜

r

...

...

...

r2 p ⎟

... ⎟.

⎟

r

⎜

⎝ p1

rp 2

...

⎟

pp ⎠

При оценке тесноты связи одной из переменных с совокупностью ос-

тальных

( p −1)

переменных используется множественный коэффициент

корреляции.

Определение 12.3. Множественным коэффициентом корреляции

X1 относительно

X 2 ,

X 3 , …,

X p называется величина, равная

R1 =

1 − det Rв ,

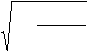R11

где

R11

– алгебраическое дополнение элемента

r11

матрицы

Rв , при этом

R

величина

2 называется множественным коэффициентом детерминации

Х1 относительно

X 2 ,

X 3 , …,

X p .

Замечание. Множественный коэффициент корреляции заключен в

пределах

0 ≤ R1 ≤1

и показывает тесноту связи, но не ее направление.

Множественный коэффициент детерминации показывает, какую долю вариа-

ции переменной

Х1 объясняет вариация остальных переменных.

Если переменные коррелируют друг с другом, то на величине коэффи- циента парной корреляции частично сказывается влияние других перемен- ных. Поэтому иногда возникает необходимость исследовать частную корре- ляцию между двумя переменными при исключении влияния остальных пе- ременных.

Определение 12.4. Выборочным частным коэффициентом корре-

ляции между X i

и X j

при фиксированном значении остальных называется

величина, равная

R = − Rij ,

ij

R

⋅ R

ii jj

где

Rij ,

Rii ,

R jj

– алгебраические дополнения элементов

rij ,

rii ,

rjj

матрицы

Rв соответственно.

Для оценки значимости множественного коэффициента корреляции тре-

буется найти наблюдаемое значение критерия Фишера

мулу

Fнабл. , используя фор-

Fнабл.

R 2 (n − p)

= 1 ,

(1 − R 2 )( p −1)

и критическое значение критерия Фишера ние 6).

Fкр. (α; n −1; n − p)

(см. приложе-

Если

Fнабл. > Fкр. (α,

p−1, n − p) , то множественный коэффициент корре-

ляции значимо отличается от нуля, а это означает, что в генеральной сово-

купности имеется корреляционная зависимость

Х1 от остальных перемен-

ных. В противном случае в генеральной совокупности корреляционной зави-

симости нет.

Для оценки значимости частных коэффициентов корреляции можно ис-

пользовать ту же формулу, что и в одномерном корреляционном анализе, но

в качестве числа n взять

n′ = n− p + 2 .

Пример 12.1. Исследовалась зависимость между величиной заработ-

ной платы работников предприятия

X1 (руб.), производительностью труда

X 2 (руб.) и себестоимостью продукции Y (руб.) на пятнадцати однотипных

предприятиях региона. Данные выборки приведены в таблице.

№
xi1
xi 2
yi			11,5		7,5	7,5	8,8	2,7	7,2		6,5	5,9	9,3	10,6	9,5

Предполагая, что между этими величинами имеется линейная зависи-

мость, на уровне значимости

α = 0,05:

а) найдите модельное уравнение регрессии;

б) оцените значимость уравнения регрессии в целом;

в) сделайте прогноз значения результативного признака y при

Решение. Пусть

x1 = 2,5 ,

T

x2 = 3 .

⎛ 1 ⎜ ⎜2 1 ⎞ ⎟ 5 ⎟ ⎜ ⎝3 4 ⎟ ⎠

X = ,

Y = (6

12 11,5 1

7,5

7,5

8,8

2,7

7,2 10

6,5

5,9

9,3 10,6

9,5)T .

Тогда будем иметь:

⎛15 45

⎜

⎜

40 ⎞

⎠

⎟

⎛ 8984

⎜

⎜

−1480

−1380⎞

⎠

⎟

XT ⋅ X

= ⎜45

⎝40

116 ⎟, (X T ⋅ X )−1=

136 ⎟

⋅ ⎜− 1480

⎝− 1380

60 ⎟ ,

450 ⎟

⎛116,0 ⎞

⎜ ⎟

X T ⋅Y = ⎜403,3⎟.

⎜ ⎟

Следовательно,

r = (5,20

1,71

⎝273,8⎠

−0,98)T.

Значит, модельное уравнение регрессии имеет вид:

yˆ = 5,20 +1,71x1 − 0,98x2 .

Оценим значимость коэффициентов регрессии. Имеем

следующую расчетную таблицу:

y = 7,7 . Составим

№ xi1 xi 2 yi (y − y )2 yˆi (y − yˆ )2 2,89 5,694 0,0910 18,49 11,811 0,0357 11,5 14,44 11,076 0,1798 44,89 1,047 0,0022 7,5 0,04 6,429 1,1470 7,5 0,04 7,650 0,0225 8,8 1,21 9,120 0,1024 2,7 3,003 0,0918 7,2 0,25 7,407 0,0428 10,0 5,29 10,098 0,0096 6,5 1,44 6,672 0,0296 5,9 3,24 5,937 0,0014 9,3 2,56 9,363 0,0040 10,6 8,41 10,883 0,0543 9,5 3,24 9,855 0,1246 ∑ – – 116,0 131,43 – 1,9387

i i i

Откуда получим:

Sобщ. =131,43 ,

Sост. =1,9387 ,

Sфакт. =129,5413 .

Наблюдаемое значение критерия Фишера

Fнабл.

= 129,5413⋅12 ≈ 400 .

1,9387⋅ 2

По таблице критических точек распределения Фишера найдем критиче-

ское значение критерия:

ние регрессии значимо.

Fкр. (0,05; 2;12)=3,89 . Так как

Fнабл. > Fкр. , то уравне-

Сделаем прогноз значения результативного признака, используя модель-

ное уравнение регрессии при

yˆ = 5,2 +1,71⋅2,5 −0,98 ⋅3 = 6,6 .

x1 = 2,5 и

x2 =3 :

Теоретические вопросы и задания

1. Как найти выборочное уравнение линейной множественной регрессии по данным выборки? Как оценивается его значимость?

2. Что называется выборочным коэффициентом корреляции?

3. Что означает, что гипотеза

Н 0 :

r = 0

принимается?

4. Для чего используют множественный коэффициент корреляции? частный коэффициент корреляции? Как их определить по результатам выборки?

Задачи и упражнения

1. Исследовалась зависимость гастрономических магазинов области по уровню издержек обращения (%) и годовому объему товарооборота Y (млн руб.). Было случайным образом исследовано 50 магазинов. Результаты исследо- вания приведены в таблице.

Y X	0,5–2,0	2,0–3,5	3,5–5,0	5,0–6,5	6,5–8,0	Итого
4–6	–	–	–
6–8	–
8–10					–
10–12				–	–
12–14		–	–	–	–
Итого

а) Найдите уравнения прямых регрессии Y на X и X на Y .

б) Найдите коэффициент корреляции и оцените его значимость.

в) Проверьте значимость найденного уравнения регрессии Y на X .

г) Найдите доверительный интервал для индивидуального значения

на тех же предприятиях.

x0 = 7

Указание. Предполагается, что выборка сделана из нормальных генераль-

ных совокупностей, и между признаками X и Y имеется линейная связь.

Уровень значимости

α = 0,05 .

2. Имеются следующие данные о выработке продукции на одного работаю-

щего на фирме

X1 (шт.), браке продукции

X 2 (%) и прибыли от реализа-

ции единицы продукции (тыс. руб.) по 20 фирмам:

i	xi1	xi 2	y	i	xi1	xi 2	y	i	xi1	xi 2	y
		4,3				1,0
		5,6				2,1
		2,8				2,2				3,0
		7,1				3,3				2,7
		10,2				4,5				6,0
		3,4				6,7				7,1
		6,2				9,0

Найдите: а) парные коэффициенты корреляции; оцените их значимость; б) матрицу множественной корреляции; в) частные коэффициенты корре- ляции; оцените их значимость; г) множественный коэффициент корреляции

зависимости Y от

X1 и

X 2 ; д) уравнение линейной множественной регрес-

сии и оцените его значимость; е) доверительный интервал для значения y0

при

x1 =15 ,

x2 =3,6 . Сделайте экономические выводы. Уровень значимо-

сти примите

α = 0,05.

Домашнее задание

1. Исследовалась зависимость производительности труда Y (т/ч) от уровня энерговооруженности X (%) для однотипных предприятий региона. Было обследовано 60+а предприятий (а – число букв в фамилии). Результаты приведены в таблице.

Y Х	(0-4,5)	(4,5-9,0)	(9,0-13,5)	(13,5-18,0)	(18,0-22,5)	Итого
(0-1,4)			–	–	–
(1,4-2,8)			–	–	–
(2,8-4,2)				–	–
(4,2-5,6)	–		14+а		–	19+а
(5,6-7,0)	–	–	–
(7,0-8,4)	–	–	–
Итого			15+а			51+а

а) Найдите уравнения прямых регрессий X на Y , Y на X и исследуйте их

на значимость (α

= 0,05 ). б) Вычислите коэффициент корреляции

rв , оце-

ните его на значимость ( α = 0,01). в) Определите доверительный интервал

для генерального коэффициента корреляции ( γ

= 0,95 ).

2. В результате 10 экспериментов были получены следующие значения трех показателей:

№
xi1	2,0	2,2	2,4	2,6	2,8	3,0	3,2	3,4	3,6	3,8
xi 2	10,1	10,0	9,8	9,8	9,6	9,5	9,2	8,5	8,4	8,3
xi3	0,5	0,6	0,3	0,1	-0,2	-0,1		0,1	0,5	0,3

Найдите: а) парные коэффициенты корреляции; б) матрицу множественной корреляции; в) частные коэффициенты корреляции; г) множественные ко-

эффициенты корреляции зависимости

X1 от

X 2 и

X 3 ,

X 2 от

X1 и

X 3 , X 3

от X1 и

X 2 . Оцените значимость найденных коэффициентов на уровне

α = 0,05.

Занятие 13. Компонентный и факторный анализы

В экономике часто приходится проводить анализ n различных объек- тов на основании проведенных измерений по p различным показателям. Если число p достаточно велико, то с ростом n возникает ряд проблем: во-

первых, велик объем информации, а во-вторых, из нее трудно извлечь не-

кую суть, необходимую для принятия решения.

Сократить размерность можно за счет выбора новых q показателей, ко- торые, естественно, должны обеспечить наибольшее сохранение информа- ции, имеющейся в исходных p показателях, и быть попарно независимыми.

Для решения этой задачи часто используются компонентный и факторный анализы.

Пусть на n объектах произведено измерение p показателей. Получен-

ная информация представлена в виде выборочной матрицы, каждая строка которой состоит из значений одного показателя для n объектов:

⎛ x11

⎜

⎜ x21

X = ⎜

⎜ L

x12

x22

L

L x1n ⎞

⎟

L x2n ⎟

⎟.

L

⎟

L ⎟

x

⎜

⎝ p1

x p 2

L x pn ⎠

Результаты компонентного и факторного анализов существенно зависят от выбора масштаба и единиц измерения показателей. Поэтому они эффек- тивны, когда величины имеют одинаковую содержательную природу и изме- рены в одних и тех же единицах. Если это невозможно, то исходные показа- тели нормируют (тем самым от ковариационной матрицы показателей пере- ходят к корреляционной).

Нормируем значения признаков, получим матрицу Z :

⎛ z11

⎜

⎜ z21

Z = ⎜

⎜ L

z11

z22

L

L z1n ⎞

⎟

L

L z2n ⎟

⎟,

z

L ⎟

где z

xi j − xi 1 n

n

s

= , =

⎜

z

⎝ p1

z p 2 L

1 n

⎟

pn ⎠

i j

i

xi ∑ xi j ,

l =1

si = ∑ ( xi j − xi ) .

n − 1 l=1

Метод главных компонент

Компонентный анализ осуществляется при помощи метода главных компонент (англ. principal components analysis, PCA), предложенного К. Пирсоном в 1901 году.

Суть метода главных компонент (компонентного анализа) состоит в том, что от исходных p показателей переходят к p их линейным комбина-

циям, для которых выполняются следующие свойства: первая главная ком-

понента

F1 – это такая линейная комбинация исходных показателей, кото-

рая из всех таких комбинаций обладает самой большой дисперсией, т.е. при переходе от объекта к объекту меняется сильнее всего; вторая главная ком-

понента F2

– это такая комбинация показателей, которая не коррелирована с

первой и среди таких комбинаций обладает наибольшей дисперсией и т.д.;

Fp – такая линейная комбинация исходных показателей, которая не коррели-

рована с

F1 ,

F2 , …,

Fp−1 .

Таким образом, модель метода главных компонент имеет вид:

F = A⋅ Z ,

где A – матрица коэффициентов искомых линейных комбинаций.

Геометрическая интерпретация метода главных компонент в случае

p = 2

состоит в следующем: если полученные значения показателей рас-

сматривать как точки в двумерном пространстве, то множество этих точек по-разному вытянуто в различных направлениях. Первая главная компонен- та задаёт то направление, вдоль которого это множество вытянуто более всего, а вторая компонента перпендикулярна первой (рис. 13.1).

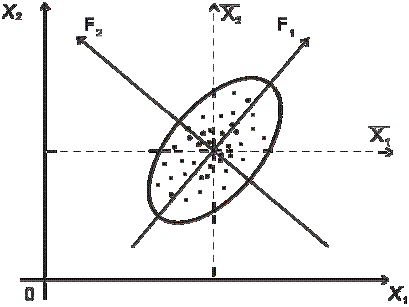Рис. 13.1

Теорема 13.1 (основная теорема компонентного анализа). Задача нахождения вектора F главных компонент совпадает с задачей поиска собственных чисел и собственных векторов корреляционной матри-

цы R вектора X исходных показателей. Если

λ1 , …, λp

– ее собственные

числа, расположенные в порядке убывания, а единичные собственные век-

торы-строки

a (1) , …,

a ( p )

отвечают этим числам, то главные компоненты

вычисляются по формулам:

Fk

= a ( k ) ⋅ X ,

k =1, 2, ..., p ,

причем их дисперсии равны соответствующим собственным числам.