Задача 2. определение реакций опор твердого тела
Жесткая рама закреплена в точке А шарнирно, а точке В прикреплена или к невесомому стержню, или к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через невесомый блок и несущий на конце груз весом Р=5кН. На раму действуют пара сил с моментом М=10 кНм и две силы, значения, направления и точки приложения которых указаны в таблице 2, а также равномерно распределенная нагрузка, интенсивность и участок распределения которой также заданы в таблице.
Определить реакции связей в точке А и В, вызываемые действующими нагрузками. При окончательных расчетах принять а=0,5м.
Таблица 2
Условия к задачи 2
| Сила | ||||||||||
| Номер варианта | 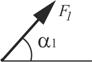 | 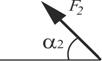 | 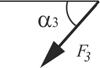 | 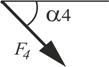 | 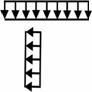 | |||||
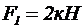 | 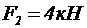 | 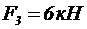 | 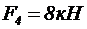 | |||||||
| Точка приложения | α1,град. | Точка приложения | α2,град. | Точка приложения | α3,град. | Точка приложения | α4,град. | Участок | Интенсивность q, кН/м | |
| Н | К | АЕ | ||||||||
| Д | Е | ВД | ||||||||
| К | Е | НС | ||||||||
| Д | Е | СК | ||||||||
| К | Н | СК | ||||||||
| Н | Д | ВД | ||||||||
| Е | К | НС | ||||||||
| Д | Н | АЕ | ||||||||
| Н | Д | ВД | ||||||||
| Е | К | АЕ |
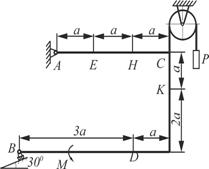 Схема 1 Схема 1 | 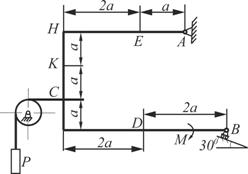 Схема 2 Схема 2 |
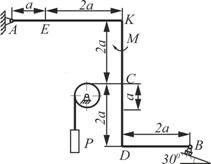 Схема 3 Схема 3 | 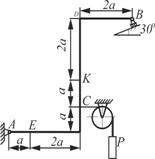 Схема 4 Схема 4 |
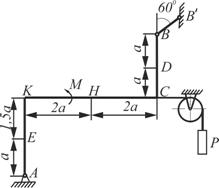 Схема 5 Схема 5 | 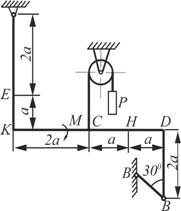 Схема 6 Схема 6 |
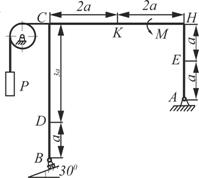 Схема 7 Схема 7 |  Схема 8 Схема 8 |
 Схема 9 Схема 9 |  Схема 10 Схема 10 |
Пример выполнения задачи 2
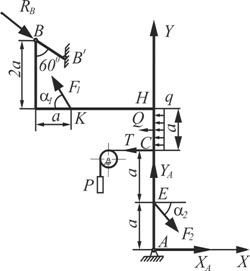 Рисунок 42 – Схема к примеру 2 Рисунок 42 – Схема к примеру 2 | Определить реакции связей в точках А и В жесткой рамы (рис. 42), нагруженной сосредоточенными силами, распределенной нагрузкой и сосредоточенным моментом. Дано: F1=2кН, F2=4кН, α1=300, α2=600,q=2кН/м, Р=5кН, М=10кНм, а=0,5м |
Рассмотрим равновесие рамы. Выбираем произвольную систему декартовых координат и изобразим действующие на раму силы F1 и F2, пару сил с моментом М, равномерно-распределенную нагрузку, интенсивности q=2кН/м, которую заменим равнодействующей силой Q, приложенной в середине участка СН:
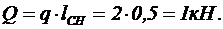
На основании принципа освобождаемости от связей заменим связи их реакциями: натяжение троса Т (по модулю Т=Р), реакция стержня RВ и неподвижного шарнира ХАи YА.
Следовательно, на раму действует плоская система произвольно расположенных сил, для которой действительны три уравнения равновесия:
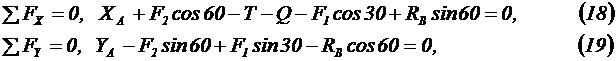
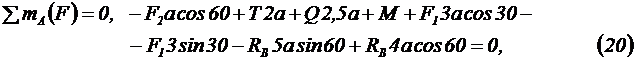
Решая уравнения относительно неизвестных реакций, получим:
ü Из уравнения (20):

ü Из уравнения (19):
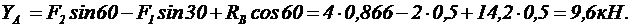
ü Из уравнения (18):
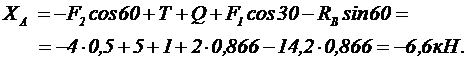
Знак «минус» показывает, что действительное направление реакции противоположно показанному на чертеже.
Задача 3. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ СВЯЗЕЙ КОНСТРУКЦИИ, СОСТОЯЩЕЙ ИЗ ДВУХ ТЕЛ
Конструкция состоит из двух частей, соединенных между собой шарниром С. Внешними связями, наложенными на конструкцию, являются жесткая заделка в точке А, а в точке В подвижный шарнир или стержень.
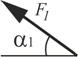
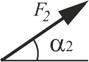
На каждую конструкцию действует пара сил с моментом М=60кНм, равномерно распределенная нагрузка, интенсивностью q=10кН/м и две силы, значения, направления и точки приложения которых указаны в таблице 3, там же указан участок, на котором действует распределенная нагрузка.
Определить реакции связей в точке А и В, вызываемые действующими нагрузками. При окончательных расчетах принять а=0,5м.
Таблица 3
Условия к задачи 3
| Номер варианта | Сила |  | |||||||
 |  | 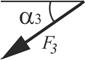 | 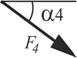 | ||||||
| F1=10кН | F1=20кН | F1=30кН | F1=40кН | ||||||
| Точка приложения | α1,град. | Точка приложения | α2,град. | Точка приложения | α3,град. | Точка приложения | α4,град. | Участок | |
| Н | К | СК | |||||||
| L | К | АЛ | |||||||
| К | L | ЛС | |||||||
| Н | L | ВД | |||||||
| К | Н | ЛС | |||||||
| К | Д | СК | |||||||
| Д | К | АЛ | |||||||
| Л | Н | ВД | |||||||
| Н | Д | СК | |||||||
| Д | Л | ВД |
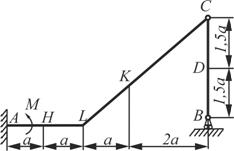 Схема 1 Схема 1 | 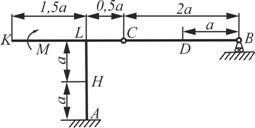 Схема 2 Схема 2 |
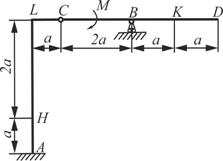 Схема 3 Схема 3 | 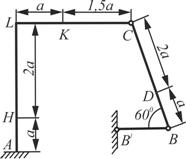 Схема 4 Схема 4 |
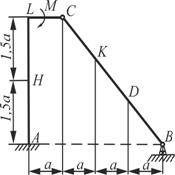 Схема 5 Схема 5 | 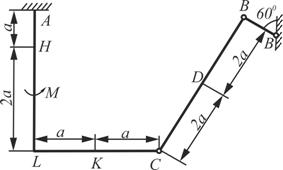 Схема 6 Схема 6 |
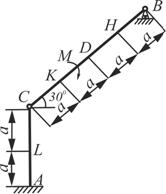 Схема 7 Схема 7 | 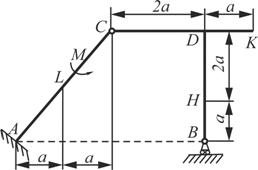 Схема 8 Схема 8 |
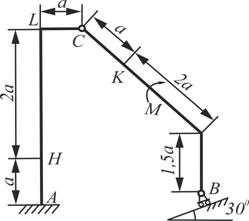 Схема 9 Схема 9 | 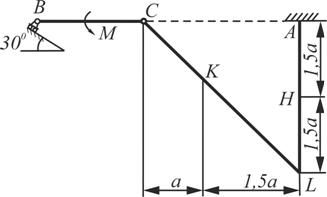 Схема 10 Схема 10 |
Пример выполнения задачи3
| На угольник АВС (угол АВС=90°), конец А которого жестко заделан, в точке С опирается на стержень DE (рис. 43). Стержень имеет в точке D неподвижную шарнирную опору и к нему приложена сила F, а к угольнику – равномерно распределенная на участке КВ нагрузка интенсивностью q и пара сил с моментом М. Дано:F=10 кН, М=5 кН×м, q=20 кН/м, а=0,2 м. | 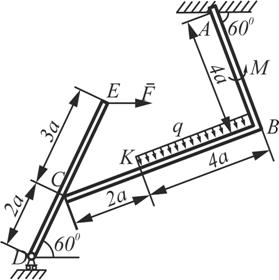 Рисунок 43 – Схема к примеру 3 Рисунок 43 – Схема к примеру 3 |
Определить реакции в точках А, С, D, вызванные заданными нагрузками.
Решение:
| 1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DE (рис. 44). Проведем координатные оси ху и изобразим действующие на стержень силы: силу F, реакцию N, направленную перпендикулярно стержню, и составляющие ХD и YD реакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия: | 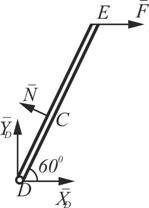 Рисунок 44 – Схема для определения усилий в стержне DE Рисунок 44 – Схема для определения усилий в стержне DE |
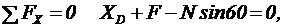
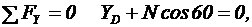
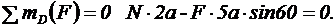
2. Теперь рассмотрим равновесие угольника (рис. 45).На него действуют сила давления стержня N, направленная противоположно реакции  , равномерно распределенная нагрузка, которую заменяем силой Q, приложенной в середине участка КВ (численно Q=4а q=16 кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из реакции, которую представим составляющими ХА, YА и пары сил с моментом МА. Для этой плоской системы сил тоже составляем три уравнения равновесия: , равномерно распределенная нагрузка, которую заменяем силой Q, приложенной в середине участка КВ (численно Q=4а q=16 кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из реакции, которую представим составляющими ХА, YА и пары сил с моментом МА. Для этой плоской системы сил тоже составляем три уравнения равновесия: | 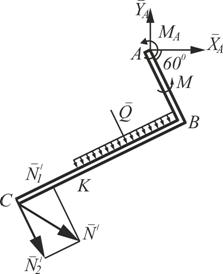 Рисунок 45 – Равновесие угольника СВА Рисунок 45 – Равновесие угольника СВА |
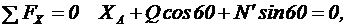
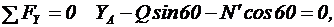
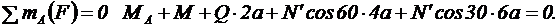
При вычислении момента силы 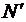 разлагаем ее на составляющие N1 и N2 и применяем теорему Вариньона. Подставим в составление уравнения числовые значения заданных величин и, решив систему из шести уравнений, найдем искомые реакции. При решении учитываем, что
разлагаем ее на составляющие N1 и N2 и применяем теорему Вариньона. Подставим в составление уравнения числовые значения заданных величин и, решив систему из шести уравнений, найдем искомые реакции. При решении учитываем, что 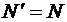 в силу равенства действия и противодействия.
в силу равенства действия и противодействия.
Ответ:N=21,7кН, YD= – 10,8кН; ХD=8,8кН, ХА= – 26,8кН, YА=24,7кН, MА=– 42,6кНм.
Знаки указывают, что силы YD,ХА и момент МА, направлены противоположно показанным на рисунках.
