Расчет задачи в онлайн программе

«Расчет рамы, фермы, балки онлайн»

1. Для доступа к программе «Расчет рамы, фермы, балки онлайн» необходимо ввести в адресной строке вашего браузера http://rama.sopromat.org (рис. 30).

Рисунок 30 – Адресная строка

2. На главной странице сайта выбираем пункт «Начать расчет рамы, фермы» (рис. 31).

Рисунок 31 – Главная страница

3. В зависимости от размеров стержней назначаем шаг ячейки. Для этого в разделе «Настройки» вводим удобный для построения шаг ячейки. В нашем случае шаг принимаем равный 0,1м(рис. 32).

Рисунок 32 – Назначение шага ячейки

Настройки программы по умолчанию позволяют производить расчет с учетом деформации (продольного сжатия-растяжения) стержней. Однако при решении задач дисциплины «Теоретическая механика» рассматривают абсолютно твердые, т.е. недеформируемые тела. Поэтому учет деформаций будет вносить ошибку при определении реакций и усилий в стержнях. В соответствии с рекомендациями авторов программы для расчёта недеформируемых тел, в разделе «Настройки» необходимо задать параметр Площадь сечения F как можно большим, например равным 100000. Для подтверждения введенных параметров нажимаем кнопку Применить.

4. Для построения стержней используем команду Добавить стержень (рис. 33).

Рисунок 33 – Построение стержневой системы

В графическом поле, имеющем сетку с назначенным шагом, строим стержни заданной длины. Контролировать размер стержней позволяет параметр Длина стержня, изменяющийся в зависимости от положения курсора и находящийся сверху графического окна.

В результате построения каждого стержня в разделе Элементы появляется соответствующая строка с параметрами элемента.

Выстраивая последовательно стержни (рис. 16), получаем плоскую ферму (рис.34), а в разделе Элементы список стержней и соответствующих им узлов. В случае ошибки в построении элемента, его можно удалить при помощи кнопки Удалить 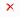и построить заново.

Рисунок 34 – Геометрическая схема фермы

5. Редактируем способ соединения в узлах фермы. Чтобы задать в узле А неподвижный шарнир (рис.16), в разделе Элементы выбираем Узел 1. В открывшемся окне в пункте Связь с землей выбираем Шарнир. Для подтверждения команды нажимаем кнопку Применить (рис. 35).

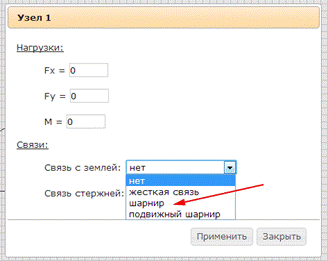
Рисунок 35 – Редактирование шарниров

В результате данной операции на чертеже в узле 1 появится неподвижный шарнир (рис. 36). Чтобы задать в узле В подвижный шарнир (рис.16), в разделе Элементы выбираем Узел 3 ив пункте Связь с землёй выбираем Подвижный шарнир. В случае подвижного шарнира существует возможность регулирования угла наклона опорной поверхности (рис. 37).

Рисунок 36 – Неподвижный шарнир

Рисунок 37 – Регулирование угла наклона

Для всех оставшихся промежуточных узлов в пункте Связь стержней выбираем Шарнир, например, узел 2 (рис. 38).

Рисунок 38 – Редактирование узлов

6. Внешнюю нагрузку задаем в разделе Элементы, выбирая узел, соответствующий точке приложения силы. В нашем примере это узел 4. В открывающемся окне авторы программы предлагают задавать силу по осям координат F_Хи F_У. В случае, когда сила приложена под углом к осям координат в пункте F_Х, вводим проекцию силы Р на ось Х и соответственно в пункте F_У вводим проекцию силы Р на ось У (рис.39). Согласно заданию (рис.16) определим проекции силы Р на координатные оси Х и У:

P_X=P·cosβ=5·cos30=4,4 кH,

P_Y=P·sinβ=5·sin30=2,5 кH.

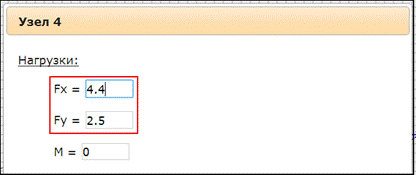
Рисунок 39 – Задание внешней нагрузки

7. Для определения реакций связей в разделе Расчет выбираем пункт Реакции опор. В результате на схеме в соответствующих узлах отобразятся значения реакций опор (рис.40).

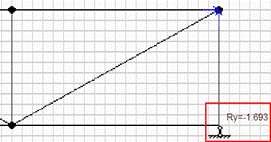
Рисунок 40 – Определение реакция связей

В результате программного расчета реакция в шарнире В равна R_B=–1,693кН, что лишь на 0,013кН отличается от результата аналитического расчета. Ошибка составляет в данном случае 0,7%. Реакцию в шарнире А программа выдает в виде проекций на координатные оси, поэтому чтобы сравнить ее с результатами аналитического расчета, надо определить модуль реакции.

.

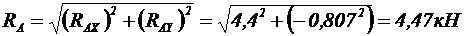Разница по сравнению с аналитическим расчетом (R_А=4,4кН) составляет 1,5%.

8. Для определения продольных усилий в стержнях в разделе Расчет выбираем Эпюра N. В результате на схеме отобразятся графики распределения усилий для каждого стержня. Стержни, на которых отсутствуют графики, соответствуют нулевым усилиям (рис.41).

Рисунок 41 – Эпюры продольных усилий

Сравнивая результаты программного расчета усилий в стержнях видно, что знаки и величины соответствуют результатам аналитического расчета. Например, в результате аналитического расчета в первом стержне усилие S₁=–1,68кН, а по результатам численного расчета S₁=–1,674кН. Разница полученных результатов составляет 0,014кН (0,83%).

Расхождение результатов аналитических расчетов и численных расчетов является следствием погрешности построения геометрии стержневой системы, так как величина шага графического поля ограничена возможностями данной программы.