Матричная форма записи графа

3.3.1.Матрица смежности

Граф можно задать матрицей смежности

V = ||v_ij||, где

v_ij = 1, если граф содержит ребро (i, j);

v_ij = 0, в противном случае.

Например, граф структурной схемы системы менеджмента качества, изображенный на рис.3.2 можно представить в виде следующей матрицы смежности.

(матрица)

3.3.2.Матрица инциденций

Используются и другие формы матричной записи графов. Например, в виде матрицы инциденций

W = ||w_ij||, где

1, если i – начальная вершина ребра (i, j);

w_ij = -1, если i – конечная вершина ребра (i, j);

0 в остальных случаях.

Например, для графа на рис.3.2 матрица инциденций будет выглядеть следующим образом.

(матрица)

Если граф не ориентирован, то матрица инциденций содержит только 0 и 1.

w_ij = 1, если имеется ребро (i, j);

w_ij = 0 в обратном случае.

Списковая форма записи графа

Большое число нулей в матрице смежности и инциденций свидетельствует о неэкономичности этих форм представления графов, что особенно существенно, если графы содержат много вершин. Поэтому помимо матриц используются списковые формы записи графов. Список представляет собой множество

R = [R(i)], где

R(i) R – есть множество вершин графа, в которые можно непосредственно попасть из i-ой вершины.

Например, в графе структуры менеджмента качества, показанной на рис.3.2 можно представить следующим списком.

R_3.1 = [R(О)={Р}, R(Р)={Ц}, R(Ц)={И,У}, R(И)={О}, R(У)={П},

R(П)={Т}, R(Т)={Ц}]

Эту запись можно упростить, если элементы множеств R(i) записать в круглых скобках, перед которыми поставить номер (обозначение) i: R = [О(Р), Р(Ц), Ц(И,У), И(О), У(П), П(Т), Т(Ц)]

Анализ структуры системы

Описание структуры системы в виде графа дает возможность провести анализ структуры системы и оценить ее качество. Рассмотрим следующие основные задачи анализа структур.

Анализ элементов

При исследовании структуры особое значение имеет выделение элементов, соответствующих изолированным, висячим и тупиковым вершинам графа. Изолированные вершины не инцидентны ни одному из ребер графа; висячие соответствуют вершинам, в которые нельзя попасть ни из одной другой вершины графа; тупиковые соответствуют вершинам, из которых нельзя попасть в другие вершины графа. В качестве примера рассмотрим граф на рис.4.1.

Рис.4.1 Фрагмент структуры системы

Граф на рис.4.1 содержит изолированную вершину 12, висячие вершины 1, 2, 3 и ни одной тупиковой вершины. Если соединить вершину 12 с вершинами 11 и 8, то она превратиться в тупиковую. Изолированные, висячие и тупиковые вершины на графе отыскиваются следующим образом:

Берется матрица смежности графа V = ||v_ij||;

По этой матрице для каждой вершины k (k = 1, 2, … , n), где n – число вершин в графе, определяется вектор v(k) = (v_k, v^k) с компонентами

v_k = 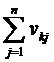, v^k = 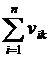, где

v_k – сумма элементов k-ой строки матрицы V, определяющее число ребер, выходящих из вершины k,

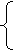v^k – сумма элементов k-го столбца матрицы V, определяющее число ребер, входящих в вершину k

v_k = v^k = 0, то вершина k изолированная;

Если v_k = 0, то вершина k тупиковая;

v^k = 0, то вершина k висячая.

Что дает анализ элементов?

а. Наличие в графе изолированных вершин обычно свидетельствует об ошибках, допущенных при формировании или описании структуры, ведь система всегда целостный объект, все элементы которого взаимосвязаны;

б. Висячие вершины должны соответствовать входным элементам системы (вход системы);

в. Тупиковые вершины должны соответствовать выходным элементам системы (выход системы);

г. Через висячие и тупиковые вершины осуществляется процесс взаимодействия системы с внешней средой, поэтому очень важно, чтобы путем исследования графа они были правильно интерпретированы.

Анализ связи

Исследование связи между элементами структуры направлено, прежде всего, на выявление в соответствующем графе петель, контуров и сильносвязаных подграфов. Например, граф на рис.4.1 имеет петлю у вершины 11 и два контура, образованные ребрами, соединяющие вершины (4, 5, 6, 9) и (6, 9, 10, 11).

Подграф называется сильносвязным, если все входящие в него вершины взаимодостижимы, т.е. из любой вершины подграфа можно попасть в любую другую его вершину.

2.1.Выделение из графа сильносвязного подграфа

Пусть Q_i – множество вершин графа, достижимых из вершины , а Qⁱ – множество вершин графа, из которых можно достичь вершину .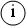

Из определения сильносвязного подграфа следует, что пересечение множеств Q(i) = Q_i∩Qⁱ содержит вершины, принадлежащие одному сильносвязному подграфу, поэтому нахождение пересечения Q(i) равносильно определению сильносвязного подграфа, включающего в себя вершину .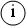

Последовательно перебирая 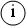и определяя множества Q(i) до тех пор, пока в эти множества не войдут все вершины графа, можно найти его разбиение на сильносвязные подграфы.

2.2.Пример определения сильносвязного графа

Для графа на рис.4.1 найдем его сильносвязные подграфы путем определения следующих пересечений множеств.

Q(1) = {1, 4, 5, 6, 9, 10, 11} ∩ {1} = {1}

Q(2) = {2, 5, 4, 6, 9, 10, 11, 7} ∩ {2} = {2}

Q(3) = {3, 7, 6, 9, 10, 11, 8} ∩ {3} = {3}

Q(4) = {4, 5, 6, 9, 10, 11} ∩ {1,…,11} = {4, 5, 6, 9, 10, 11}

Q(6) = Q(5) = Q(4)

Q(7) = {4, 5, 6, 7, 9, 10, 11,} ∩ {2, 3, 7, 8} = {7}

Q(8) = {8}

Теперь исходный граф можно разбить на сильносвязные подграфы: G(1), G(2), G(3), G(4), G(7), G(8), G(12), из которых только G(4) является нетривиальным (содержит больше одной вершины).

2.3.Граф-конденсация

Представим найденные сильносвязные подграфы как вершины нового графа, показанного на рис.4.2

Рис.4.2. Граф-конденсация

В результате получим граф, называемый конденсацией, который значительно проще исходного и в котором отсутствуют контуры и петли. Построение конденсаций рекомендуется для сложных структур, содержащих большое число элементов. Непосредственное исследование таких структур затруднено, а выделение конденсаций позволяет сосредоточить внимание на анализе существенных связей в наибольшей степени характеризующих особенности взаимодействия элементов системы.

Диаметр структуры

Если I и J – множество висячих и тупиковых вершин графа соответственно, то диаметр структуры определяется следующей формулой

d = 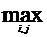d_ij,

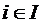
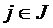, где

d_ij – длина минимального пути между висячей вершиной 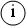и тупиковой вершиной 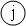равный числу ребер, составляющих этот путь.

Диаметр структуры характеризует максимальное число связей, разделяющих входные и выходные элементы структуры. По значению диаметра d можно косвенно судить о ряде предельных параметров системы, в частности о ее надежности, длительности, задержках сообщений, идущих от висячих вершин к тупиковым, инерционности. Определение значений d_ij сводится к стандартной задаче поиска кратчайшего пути на графе для каждой пары (i,j) такой, что , .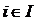

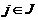Анализ структуры системы

Описание структуры системы в виде графа дает возможность провести анализ структуры системы и оценить ее качество. Рассмотрим следующие основные задачи анализа структур.

Связность

В теории графов под связностью графов понимается наименьшее число вершин, удаление которых из графов приводит а несвязному (содержащему изолированные вершины) или тривиальному (состоящему из одной вершины) графу. Используется также понятие реберной связности - наименьшего числа ребер, удаление которых приводит к несвязному или тривиальному графу. Обе характеристики достаточно сложно вычислить, еще сложнее дать им подходящую физическую интерпретацию, поэтому ограничимся только определением понятия «связность».

Степень централизации

Эта характеристика (критерий качества) структуры применяется для оценки неравномерности загрузки элементов структуры путем вычисления индекса центральности β. Пример показан на рис.4.3

Рис.4.3.а) связи в структуре распределены равномерно β = 0

Рис.4.3.б) структура с максимальной степенью централизации β = 1

Индекс центральности для неориентированного графа вычисляется по следующим формулам

β = (n-1)(2∙z_max-n)/z_max(n-2), где

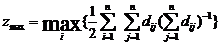
причем для всех i = j естественным образом длина минимального пути d_ij = 0

Сложность

Понятие сложности структуры с трудом поддается формализации и имеет субъективный оттенок. Сложность структуры будем определять сложностью анализа ее свойств. Если функционирование системы представить себе как процесс переработки входных воздействий в выходные, направленные соответственно от входных элементов системы к входным, то можно предположить, что изучать свойства этого процесса будет тем труднее, чем разнообразнее пути, ведущие от входа к выходу системы. Взяв это предположение за основу, показатель (критерий сложности) можно вычислить по следующей формуле.

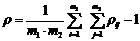
m₁ и m₂ – число висячих и тупиковых вершин в графе структуры;

ρ_ij –число различных путей, ведущих от i-ой висячей в j-ую тупиковую