Зависимость веса тел от географической широты местности.

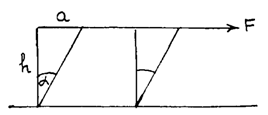
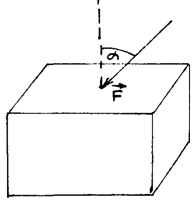
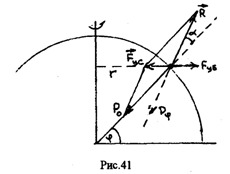Географической широтой местности называют угол между радиусом Земли, проведенным в рассматриваемую точку и экваториальной плоскостью (рис. 41).

На тело, покоящееся относительно Земли, действует сила гравитационного

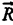
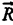Притяжения , направленная к центру Земли, и реакция поверхности . Реакция отклоняется от нормали к поверхности на угол a, чтобы равнодействующая реакции поверхности Земли R и гравитационной силы давала центростремительную силу, обеспечивающую нормальное ускорение при вращении тела вместе с поверхностью Земли.

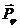Силу, равную по величине реакции и противоположно ей направленную, называют весом тела .

В системе, связанной с Землей, тело покоится, поэтому необходимо ввести центробежную силу инерции .

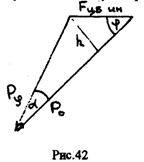
Из силового треугольника, представленного на рис.42, можно определить величину веса тела на географической широте j и угол отклонения a силы веса тела от радиуса Земли.

Центробежная сила инерции равна:

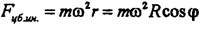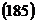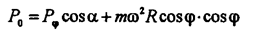С учетом этого получим:

т.е

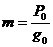Так как угол a мал, а , получим окончательно:

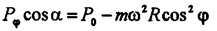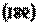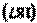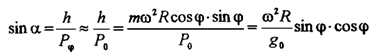Угол отклонения a легко определить из рис.42.

Как видно из (167) и (168), вес тела максимален на полюсах и минимален на экваторе. Отклонение силы веса от радиуса Земли максимально на широте p/4 и равно нулю на полюсах и экваторе.

Силы трения. Сухое трение. Силы трения скольжения.

Сухим (внешним) трением называют силы сопротивления движению , возникающие при относительном двжении одного твёрдого тла по поверхности другого. Силы сопротивления движению определяются наличием микро- и макронеровностей поверхностей трущихся тел и взаимодействием между ими. При скольжении одной твёрдой поверхности по другой в плоскости соприкосновения тел возникают силы, направленные противоположно относительной скорости. Эти силы и называют силами трения скольжения. Основные законы и закономерности для сил трения скольжения получены опытным путём. Закон кулона определяет величину сил трения скольжения:

Fтр = k*N,

Где: Fтр – сила трения скольжения, N – нормальная составляющая реакции поверхности, k – коэффициент трения скольжения. Коэффициент трения скольжения K является безразмерной величиной и определяется природой и состоянием поверхностей трущихся тел. Кроме закона Кулона опытным путём установлен ряд закономерностей для трения скольжения среди которых наиболее часто употребляются следущие:

1. При попытке сдвинуть одно тело по поверхности другого в плоскости контакта возникают силы сопротивления, изменяющиеся от нуля до предельного значения, называемого силой трения покоя.

2. С увеличением относительной скорости трущихся тел силы трения сначала убывает , а затем начинают возрастать.

3. Силы трения тем меньше, чем твёрже трущиеся поверхности.

Силы трения качения.

Трение качения возникает при качении одного твердого тела по поверхности другого. При попытке сдвинуть тело по поверхности другого в плоскости соприкосновения возникает

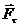сила препятствующая этому (рис. 43).

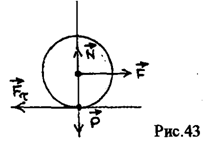Положим, что оба тела являются абсолютно твердыми, недеформируемыми, В этом случае нормальная составляющая реакции проходит через точку касания и центр масс катка (считаем его однородным симметричным телом, например, цилиндром). При такой модели любая по величине сила может вызвать качение катка, т.е. сопротивление движению.

не возникает. Более того, сила должна вызывать угловое ускорение при любой по величине силе , что противоречит опыту.

Сопротивление качению может возникать в том случае, если нормальная реакция смещается относительно вертикального диаметра катка в сторону движения. Это происходит в том случае, если давление катка на поверхность будет не в точке, а по участку поверхности, а интенсивность давления будет больше впереди вертикального диаметра катка, как показано на рис. 44.

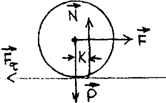Рис.44

Следовательно, поверхность должна деформироваться, причем деформации будут несимметричными относительно вертикального диаметра.

Положим, что сила 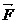вызывает равномерное качение катка, т.е.

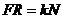
Откуда

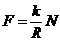(190)

Здесь 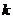(коэффициент трения качения) является размерной величиной. Смысл его- ''плечо'' нормальной составляющей реакции поверхности.

24. 1Вязкое трение

Вязкое трение возникает при относительном движении слоёв жидкости или газа. Основные законы вязкого трения получены опытным путём.

Ньютон установил, что если под действием силы площадка 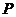площади 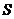движется равномерно со скоростью 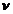относительно площадки 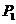(рис.45),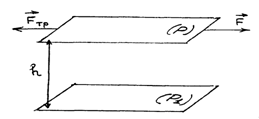

Рис.45

На подвижную площадку действуют силы сопротивления движению (силы вязкого трения):

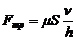
где 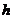- расстояние между площадками (слоями), 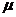- коэффициент вязкого трения определяемая свойствами вязкой среды, заполняющей промежуток между площадками.

При движении тел в вязкой среде на них действуют силы сопротивления движению.

Стокс получил выражение для этих сил. При малых скоростях.

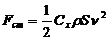(192)

где: 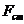- стоксова сила сопративления, 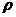- плотность среды, 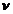- скорость тела, 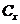-коэффициент, определяемый геометрией тела, 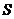- площадь проекции тела на плоскость, перпендикулярную направлению движения.

24.2Движение тел в сопротивляющейся среде.

При достаточно больших скоростях тел (или если форма тела является плохо обтекаемой) силы Стокса становятся пропорциональны квадрату скорсти:

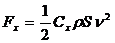
Положим, что тело начинает падать под действием силы тяжести в сопротивляющейся среде. Пренебрегая силой Архимеда, запишем:

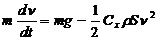
С течением времени скорость тела возрастает, возрастает и сила Стокса. Наконец, силы тяжести и Стокса уравновешиваются, после чего начинается равномерное движение тела с установившейся скоростью 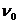. Определим зависимость скорости от проходимого телом пути и значение установившейся скорости. Для этого сначала преобразуем (194):

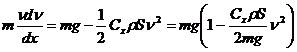
Обозначим: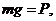

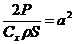
Тогда: 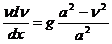Или: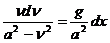

Интегрируя (195), получим: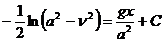

Константу интегрирования находим из начальных условий (x=0 и 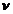=0):

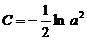
Подставив (197) в (196) получим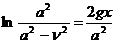

Или: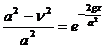

Откуда: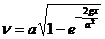

Через достаточно большой промежуток времени ( 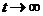) скорость тела перестаёт изменяться. Следовательно, значение установившейся скорости равно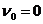

(178) и (179) и дают искомое решение поставленной задачи.

25.1 Упругие силы.

Упругостью называют свойство восстанавливать времменно утраченную форму и объём, а деформациями- само изменение формы и объёма тела. Причиной упругости является наличие одновременно присутствующих сил взаимодействия между частицами тела- притяжения ( 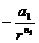) и отталкивания ( 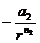). Равнодействующая этих сил равна:

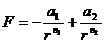(200)

На рис.46 представлены графики силы взаимного отталкивания (1), притяжения (2) и равнодействующая этих сил (3). На расстоянии 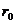между взаимодействующими частицами равнодействующая равна нулю (положение равновесия). При 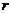< 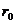преобладают силы отталкивания, а при 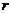> 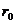силы притяжения.

Потенциальная энергия взаимодействия на расстоянии 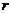между частицами:

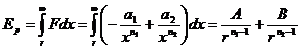(201)

где: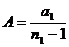

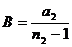
Графики потенциальной энергии сил отталкивания (1), притяжения (2) и равнодействующей (3) представлены на рис.47:

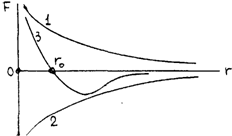
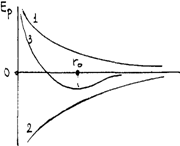
Рис.46 Рис.47

25.2Продольное сжатие и растяжение.

Закон Гука.

При продольном сжатии или растяжении одного упругого образца длинны 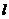и площади сечения 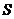удлинение образца 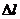определяется из опыта выражением:

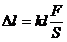(202)

где 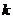- коэффициент упругости, определяемый свойствами материала образца.

Величина 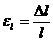называется относительной деформацией. Величина 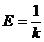, обратная коэффициенту упругости, называется модулем упругости Юнга.

С учётом этих обозначений закон Гука для деформации продольного сжатия или растяжения имеет вид:

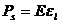(203)

где 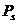- называется напряжением (отношение упругих сил в деформированном образце к площади его поперечного сечения).

При изменении продольных размеров одновременно и поперечные. Изменение 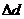диаметра 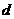образца (однородного цилиндра) также подчиняется закону Гука:

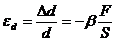(204)

где: 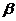-коэффициент поперечного сжатия при продольном растяжении.

Сравнивая (203) и (204) получим:

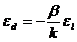(205)

Величина 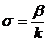называется коэффициентом Пуассона.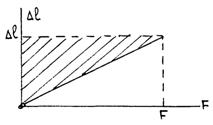

Рис.48

Если деформирующая сила изменяется от нуля до 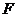, абсолютная деформация изменяется, соответственно, от нуля до 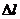то образец приобретает потенциальную энергию упругих деформаций, численно равную работе деформирующей силы. Эта работа равна площади заштрихованной фигуры (рис.48), т.е:

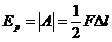
Используя закон Гука, получим:

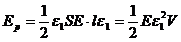
А плотность энергии, соответственно: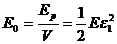

Деформация сдвига

Деформация сдвига возникает при действии на тело касательных усилий (рис. 49). Если к верхней грани образца, имеющего форму параллелепипеда, приложена касательная сила 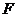, распределённая по грани площади 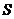, грань сдвигается на расстояние 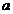, которое называется абсолютной деформацией при сдвиге.

(рис 49)

Относительной деформацией называют отношение абсолютной деформации 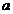к поперечным размерам 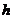. Для сдвига закон Гука принимает форму:

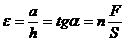(208)

где 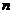-коэффициент сдвига, определяемый свойствами материала образца, величина, обратная 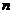, называется модулем сдвига:

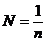
Поскольку упругие деформации, для которых формулируется закон Гука, имеют место только при маленьких значениях деформации, закон Гука для сдвига принимает вид:

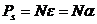(209)

26.2Деформация кручения.

Деформации кручения возникают при закручивании одного основания образца

относительно другого .

По закону Гука для этого типа деформации:

(210)

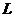где - угол закручивания, - длинна образца, 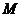- момент закручивающих сил, 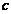- коэффициент кручения.

Величина 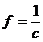называется модулем кручения т. е.

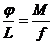(211)

Одновременно с закручиванием образца происходит сдвиг его слоёв. Угол сдвига 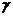определяется из закона Гука.

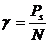(212)

Угол сдвига можно получить и из чисто геометрических соображений:

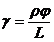(213)

Сравнивая (212) и (213), получим

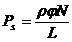(214)

Момент распределённых сил, приложенных к нижнему основанию образца, получим, используя (214)

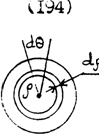
Рис.51

Из рис.51 видно, что элементарный момент закручивающих сил, приложенных к элементу основания, равен:

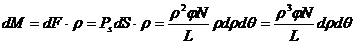(215)

Полный момент:

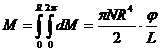(216)

Сравнивая (210) и (216), получаем связь между модулями сдвига и кручения:

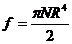
27. Закон всемирного тяготения.

Закон всемирного тяготения получен Ньютоном из наблюдений видимого движения планет Солнечной системы, используя законы динамики. В векторной форме закон всемирного тяготения, определяющий силы гравитационного взаимодействия, имеет вид:

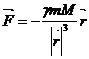(218)

где 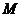- масса источника гравитационного поля, 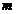- величина пробной массы, 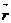-радиус-вектор точечной пробной массы относительно центра масс источника поля, 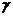- гравитационная постоянная.

Силовой характер поля источника является сила, действующая на единичную пробную массу, помещённую в данную точку поля. Эта величина называется напряжённостью поля:

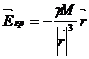(219)

Следует отметить, что закон всемирного тяготения справедлив только для точечных взаимодействующих масс. Кроме того, массы тел, фигурирующие в законе всемирного тяготения, имею другой смысл, нежели в законах динамики. Это –“тяготеющие”,”тяжёлые” или ”гравитационные” массы.

28.1 Потенциальная энергия гравитационного взаимодействия, гравитационный потенциал.

Потенциальная энергия взаимодействия численно равна работе сил взаимодействия по перемещению взаимодействующего тела из данного положения в бесконечность:

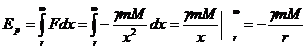(220)

Энергетической характеристикой поля является гравитационный потенциал, равный потенциальной энергии единичной пробной массы, помещённой в данную точку поля:

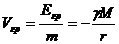(221)

28.2Связь напряжённости и потенциала поля.

На расстояниях 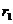и 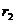от источника поля напряжённости поля равны:

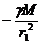и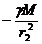

В этих же точках определим потенциалы:

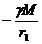и

И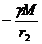зменение потенциала на еденицу длинны:

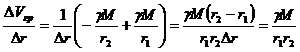
Если точки расположены бесконечно близко друг к другу, связь напряжённости и потенциала принимает вид:

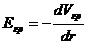(222)

Работа и энергия

Работой силы называют величину, равную произведение силы на перемещение точки приложения силы:

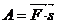(235)

Как видно, если сила и перемещение взаимно перпендикулярны, работа силы равна нулю. Например, центростремительная сила не производит работы, ее роль сводится лишь к искривлению траектории.

Работа суммы сил равна сумме работ, производимых отдельными силами системы. Например:

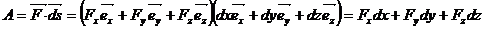(236)

Работа силы тяжести.

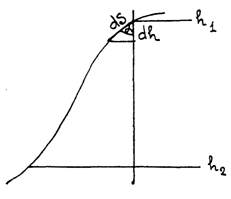
Рис.54

Пусть тело под действием силы тяжести скользит по наклонной поверхности произвольной формы (рис.54.) работа нормальной реакции по (235) равна нулю, поэтому при отсутствии трения работу совершает только сила тяжести. На элементарном перемещении работа 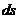силы равна:

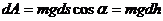(237)

Следовательно, на конечном перемещении работа сил тяжести не зависит от формы траектории и равна:

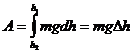
где: 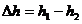перемещение тела по вертикали.

29.3Работа упругих сил.

На гладкой горизонтальной плоскости находится тело, скрепленное пружиной жесткости 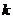с вертикальной стенкой (рис.55).

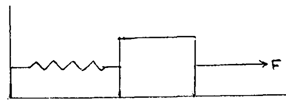
Рис.55

Если под действие внешней силы 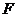пружина растягивается на 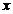, возникает сила упругости пружины, равная в пределах упругих деформаций 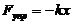. Элементарная работа упругих сил по перемещению тела из этого положения на 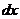равна:

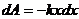
Работа же силы на конечном перемещении:

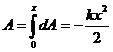(238)

где 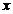– растяжение (удлинение) пружины.

30 .1 Работа и кинетическая энергия.

Если на тело массы m действует постоянная сила 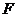, работа ее на перемещении :

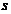т.е. равна разности кинетических энергий тела в конце и в начале перемещения.

Аналогичный результат можно получить и для переменной силы. Для этого разобьем все перемещение на малые участки, в пределах которых силу можно считать постоянной и ее работу вычислить по (239):

,

,

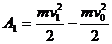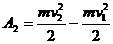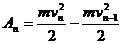
На всем перемещении работа силы равна:

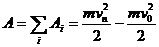(240)

Если же на тело действуют дополнительно силы трения, получаем:

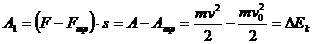(241)

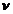где: и 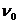- скорость тела в конце и в начале перемещения, А 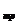- работа сил трения.

Следовательно, работа силы 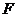равна:

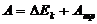(242)

30.2Работа центральных сил.

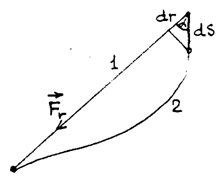
Рис.56

Если на тело действует центральная сила 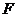(рис.56), ее работа на элементарном перемещении 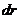вдоль линии действия силы равна (вдоль траектории1):

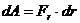(243)

а работа на конечном перемещении:

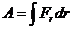(244)

При движении по произвольной траектории на элементарном перемещении работа силы выражается соотношением:

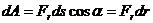
т.е. совпадает с (243). Т.е. работа центральных сил не зависит от формы траектории, а определяется лишь начальным и конечным положениями перемещаемого тела.

Силы, работа которых не зависит от формы траектории, называют консервативными. К ним, например, относятся силы упругости, силы электростатического взаимодействия между точечными зарядами, гравитационные силы, а силы трения – не являются консервативными.

30.3Потенциальная энергия.

Потенциальной энергией называют энергию, определяемую конфигурацией системы, относительным расположением отдельных взаимодействующих тел. выражение для потенциальной энергии для про­извольного взаимодействия записать сложно, обычно определяют ее изменение относительно уровня, условно принятого за нулевой. например, потенциальная энергия тела массы m в поле тяготения Земли, находящегося на высоте h над ее поверхностью:

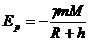
а на поверхности:

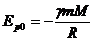
Изменение потенциальной энергии тела относительно поверх­ности Земли:

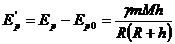(225)

При « (225) принимает вид:

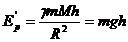
Таким выражением и пользуются, как правило, при расчетах. Здесь потенциальная энергия отсчитывается от определенного уров­ня (поверхности Земли), на которое она условно принята нулевой.

Такой подход оправдан тем, что при изменениях конфигурации сис­тем изменение состояния определяется не самим значением потен­циальной энергии, а только изменением ее.

30.3Нормировка потенциальной энергии, закон сохранения энергии.

Положим, что в замкнутой консервативной системе выделены состояния 1, 2 и 3, условно принятое за исходное, При переходе из состоя­ний 1, 2 в исходное (рис. 57) работа консервативных сил равна:

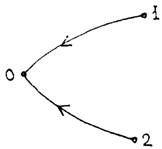
(рис. 57)

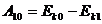(246)

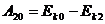(247)

откуда:

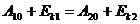(248)

Т.е. для любых состояний системы кинетическая энергия в этом состоянии и работа внутренних сил по переходу из выбранного состояния в исходное - величина постоянная для всех состояний системы. При этом знак работы определяется выбором исходного состояния. Для расчетов важно, чтобы работа сил на любом переходе имела одинаковый знак, поэтому в выражении (248) к значению работы надо добавить такую положительную величину 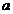, чтобы:

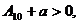
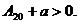
Сама проделанная операция выбора 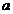называется нормировкой потенциальной энергии, а сумма 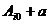- потенциальной энергией системы в данном состоянии. С учетом сказанного:

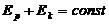(249)

для всех состояний системы. Это и есть закон сохранения механичес­кой энергии.

Пример нормировки приведен в предыдущем параграфе.

31.1Момент инерции твёрдого тела.

Для описания вращательного движения тела существенно значение его момента инерции. По определению момент инерции твердого тела равен сумме моментов инерции отдельных его частиц:

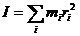
где 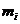- масса 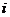-й частицы тела, 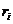- ее расстояние от заданного центра или оси.

Предположим, что масса выделенной частицы тела 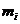, расстояние от нее до начала координат (т. о) 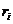, а координаты, соответственно, 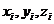(рис. 58).

Момент инерции относительно т. О по определению равен

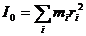(250)

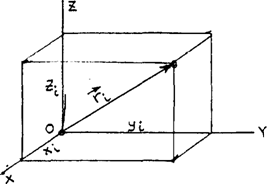
(рис. 58)

а относительно координатных осей:

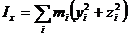(251)

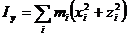(252)

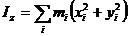(253)

Сравнивая (230), (231), (232) и (233), получим связь момен­та инерции тела относительно начала координат с моментами инерции относительно координатных осей:

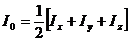(254)

Если одним из размеров тела можно пренебречь по сравнению с двумя другими (плоское тело), эта связь запишется в виде:

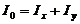(255)

31.2Теорема Штейнера.

Расчет моментов инерции тела даже правильной формы, если ось не проходит через центр масс тела, затруднен. В этом случае удобно пользоваться теоремой Штейнера:

Момент инерции тела относительно произвольной оси 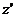равен сумме момента инерции относительно оси 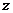, параллельной заданной и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями:

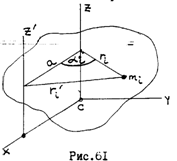
Для доказательства через центр масс тела (т. С) проведем ось 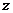, параллельную заданной оси 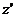(рис. 61). Расстояние между осями равно 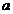. Выберем частицу тела массы 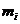, настояние от нее до осей 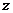и 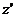указаны на рисунке.

Момент инерции тела относительно 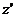по определению:

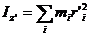(262)

Из геометрических соображений:

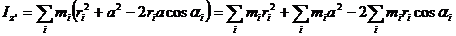
Первое слагаемое в правой части дает момент инерции тела относительно :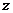

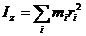(263)

Поскольку a=const, второе слагаемое принимает вид (Ma²), где М - масса тела.

В последнем слагаемом:

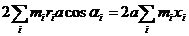
следовательно, по определению центра масс:

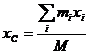
последнее слагаемое обращается в нуль, поэтому:

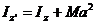
что и требовалось доказать.

32. Кинетическая энергия твёрдого тела для различных типов движения.

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ

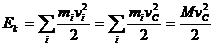(264)

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ

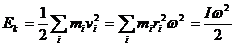(265)

ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА

В любой момент времени плоское движение можно представить, как вращение вокруг мгновенного центра вращения, пусть О -мгновенный центр вращения, а т. С - центр с масс тела. Тогда:

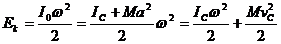(266)

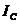где: и 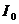- моменты инерции тела относительно осей, проходя­щих через центр масс и мгновенный центр вращения, 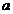- расстояние между осями, 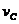. - скорость центра масс поступательной час­ти движения), (омега) - угловая скорость вращения вокруг оси, прохо­дящей через центр масс.

33.1 Гироскопы.

Рассмотрим быстро вращающийся относительно оси симметрии массивный диск (рис.64). При очень быстром вращении диска, как было сказано выше, векторы момента импульса и угловой скорости направлены вдоль оси симметрии.

Если к концам оси вращения приложить пару сил, ее момент будет изменять момент импульса в соответствии с уравнением моментов:

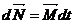
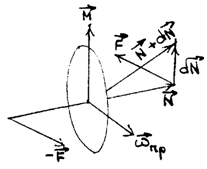
рис. 64)

Через промежуток времени 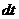момент импульса изменит свое направление и станет равным 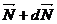Соответственно изменится и положение оси симметрии. Как видно, силы пары приложены в горизонтальной плоскости, а ось вращается под действием момента - в вертикальной.

Уравнение моментов в скалярном виде в этом случае представляют следующим образом:

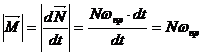
С учетом направлений векторов уравнение моментов для быстро вращающегося тела записывает в векторной форме так:

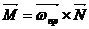(273)

Гироскопом называют массивное тело, очень быстро вращающееся вокруг оси симметрии. Наиболее часто применяются гироскопы в кардановых подвесах. В таких подвесах при любом повороте оси вращения центр масс гироскопа остается неподвижным (рис.65) Нa рисунке представлен карданов подвес для гироскопа с двумя степенями свободы.

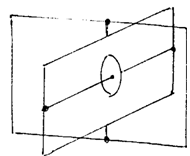
Рис.65

Для определения угловой скорости прецессии удобно пользоваться следующими соображениями. Масштаб измерения 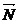можно выбрать таким, что конец вектора 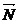совпадает с концом оси гироскопа (рис. 66).

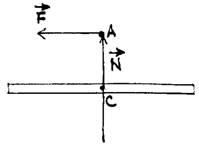
(рис. 66)

При действии на конец оси (в т. А) силы 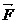ее момент вызовет прецессион­ное вращение. По уравнению моментов

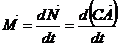
Но 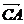можно рассматривать как радиус-вектор т. A относительно центра масс. Тогда, по определению:

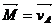(274)

33.2Прецессия волчка.

Быстро вращающийся симметричный волчок установлен на горизонтальную поверхность (рис. 67). Точка касания 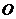неподвижна. Прецессия волчка вызывается моментом силы тяжести так как линия действия реакции проходит через неподвижный центр .

при указанном направлении вращения момент силы тяжести вызывает пре­цессию в направлении, указанном на рисунке. Угловую скорость прецессии

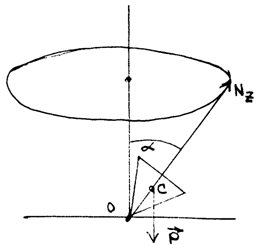
(рис. 67)

можно определить, пользуясь (274):

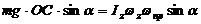
т.е.

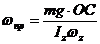(275)

Следовательно, угловая скорость прецессии тем меньше, чем больше угловая скорость собственного вращения.

34.1Давление покоящейся жидкости.

(рис.68)

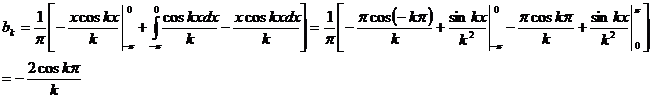
Таким образом, коэффициенты Фурье 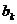при чётных значениях равны

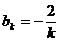(358)

а при нечётных

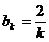(359)

С учётом найденных коэффициентов (352),(356),(358), и (359) разложение в тригонометрический ряд Фурье колебаний пилообразной формы записывается в виде

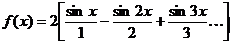(360)

в) Колебания треугольной формы

Колебания треугольной формы (рис.112) описываются функцией 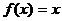, определённой в промежутке и